Слайд 15. Уравнение состояния идеального газа
(уравнение Менделеева-Клапейрона)
Идеальным газом называют
газ, молекулы которого пренебрежимо малы, по сравнению расстояниями между ними,
и не взаимодействуют друг с другом на этом расстоянии.
Все газы, при нормальных условиях, близки по свойствам к идеальному газу. Ближе всех газов к идеальному газу – водород.
Уравнение, связывающее основные параметры состояния идеального газа вывел великий русский ученый Д.И. Менделеев.
Слайд 2 Менделеев объединил известные нам законы Бойля-Мариотта, Гей-Люссака и Шарля с
законом Авогадро. Уравнение, связывающее все эти законы, называется уравнением Менделеева-Клапейрона
и записывается так:
, (15)
здесь – число молей. Для одного моля можно записать
Слайд 3Если обозначим –
плотность газа, то
(16)
Если рассматривать смесь газов, заполняющих объём V при температуре Т, тогда, парциальные давления, можно найти, как:
, , …..
Слайд 4 Согласно закону Дальтона: полное давление смеси газа равно сумме
парциальных давлений всех газов, входящих в смесь
Отсюда, с учетом вышеизложенного, можно записать
(17)
– это уравнение Менделеева-Клапейрона для смеси газов.
Слайд 5Тема . РАСПРЕДЕЛЕНИЕ ГАЗОВЫХ МОЛЕКУЛ ПО СКОРОСТЯМ И
ЭНЕРГИЯМ
1. Скорости газовых молекул. Опыт Штерна
2. Вероятность события. Понятие о
распределении молекул газа по скоростям
3. Функция распределения Максвелла
4. Барометрическая формула
5. Распределение Больцмана
6. Закон распределения Максвелла-Больцмана
Слайд 61. Скорости газовых молекул. Опыт Штерна
В средине XIX века
была сформулирована молекулярно-кинетическая теория, но тогда не было никаких доказательств
существования самих молекул. Вся теория базировалась на предположении о движении молекул, но как измерить скорость их движения, если они невидимы.
Слайд 7 Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно,
что
.
Отсюда среднеквадратичная скорость равна:
(1)
Слайд 8 Получена хорошая формула для расчета среднеквадратичной скорости, но масса молекулы
неизвестна.
Запишем по другому значение υкв:
(2)
А мы знаем, что , тогда
(3)
где Р – давление; ρ плотность. Это уже измеряемые величины.
Слайд 9 Например, при плотности азота, равной 1,25 кг/м3, при t =
0 С и
, скорости молекул азота .
Для водорода:
При этом интересно отметить, что скорость звука в газе близка к скорости молекул в этом газе. Это объясняется тем, что звуковые волны переносятся молекулами газа.
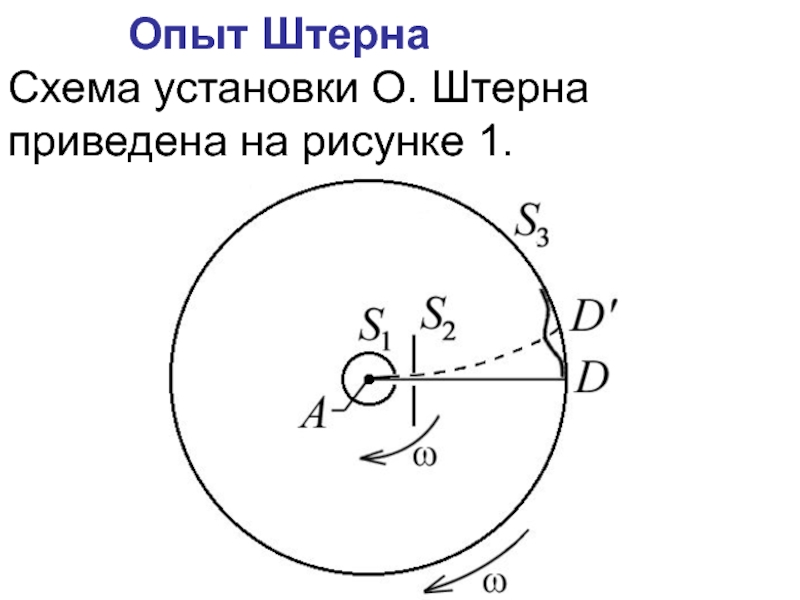
Слайд 10 Опыт Штерна
Схема установки О. Штерна приведена на рисунке 1.
Рис. 1
Слайд 11Пусть l – расстояние между D и D’, измеренное вдоль
поверхности цилиндра S3,
где – линейная скорость точек поверхности цилиндра S3, радиусом R;
время прохождения атомами серебра расстояния . Таким образом, имеем
откуда – можно определить величину скорости теплового движения атомов серебра:
Слайд 12 Температура нити в опытах Штерна равнялась 1200С, что соответствует среднеквадратичной
скорости молекул серебра
В эксперименте получился разброс значений скорости от 560 до 640 м/с. Кроме того, изображение щели D всегда оказывалось размытым, что указывало на то, что атомы Ag движутся с различными скоростями.
Слайд 13
Ещё в XIX веке Дж. Максвелл утверждал, что молекулы, беспорядочно
сталкиваясь друг с другом, как-то «распределяются» по скоростям, причём вполне
определённым образом.
Таким образом, в этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина – в хаотичности теплового движения молекул.
Слайд 142. Вероятность события.
Понятие о распределении молекул газа по скоростям
С точки зрения атомно-молекулярного строения вещества величины, встречающиеся в макроскопической
физике, имеют смысл средних значений, которые принимают некоторые функции от микроскопических переменных системы. Величины такого рода называются статистическими. Примерами таких величин являются давление, температура, плотность и др.
Слайд 15 Большое число сталкивающихся атомов и молекул обуславливает важные закономерности в
поведении статистических переменных, не свойственные отдельным атомам и молекулам.
Такие
закономерности называются вероятностными или статистическими.
Слайд 16 Математическое определение вероятности: вероятность какого-либо события – это
предел, к которому стремится отношение числа случаев, приводящих к осуществлению
события, к общему числу случаев, при бесконечном увеличении последних:
Здесь n число раз, когда событие произошло, а n общее число опытов. Отсюда следует, что Р может принимать значения от нуля до единицы.
Слайд 17 По определению Лапласа, вероятность можно представить как отношение числа благоприятных
случаев к числу возможных случаев.
Слайд 18 Определить распределение молекул по скоростям вовсе не значит, что нужно
определить число молекул, обладающих той, ли иной заданной скоростью.
Ибо число молекул, приходящихся на долю каждого значения скорости равно нулю.
Вопрос должен быть поставлен так: «Сколько молекул обладает скоростями, лежащими в интервале, включающем заданную скорость».
Слайд 19 Итак, молекулы движутся хаотически. Среди них есть и очень быстрые,
и очень медленные. Благодаря беспорядочному движению и случайному характеру их
взаимных столкновений, молекулы определённым образом распределяются по скоростям. Это распределение оказывается однозначным и единственно возможным, и не только не противоречит хаотическому движению, но именно им и обусловлено.
Слайд 21 Нам необходимо знать: сколько молекул обладает скоростями, лежащими в интервале,
включаю-щем заданную скорость?
Так всегда ставятся статистические задачи.
Например: на переписи
населения, когда указывается возраст 18 лет – это не значит, что 18 лет, 0 часов, 0 минут. Эта цифра свидетельствует, что возраст лежит в интервале от 18 до 19 лет.
Слайд 22 Мы будем искать число частиц (n) скорости
которых лежат в определённом интервале значения скорости υ ( т.е.
от υ до ).
Здесь n – число благоприятных молекул, попавших в этот интервал.
Очевидно, что в единице объёма число таких благоприятных молекул тем больше, чем больше υ.
Слайд 23 Ясно так же, что n должно быть пропорционально концентрации молекул
(n).
Число n зависит и от самой скорости, так как
в одинаковых по величине интервалах, но при разных абсолютных значениях скорости, число молекул будет различным
Смысл сказанного легко понять из простого примера: неодинаково, число людей в возрас-те от 20 до 21 года и от 90 до 91 года.
И так
Здесь f(υ) – функция распределения молекул по скоростям, n – концентрация молекул и
υ - интервал значений скоростей.
Перейдя к пределу, получим
Физический смысл f(υ) в том, что это отно-шение числа молекул, скорости которых лежат в определенном интервале скоростей, к общему числу молекул в единичном интервале скоростей:
(4)
Слайд 25 Таким образом, f(υ) – имеет смысл
вероятности, то есть показывает, какова вероятность любой молекулы газа в
единице объёма иметь скорость, заключённую в единичном интервале, включающем заданную скорость υ.
В данном случае f(υ) называют плотностью вероятности.
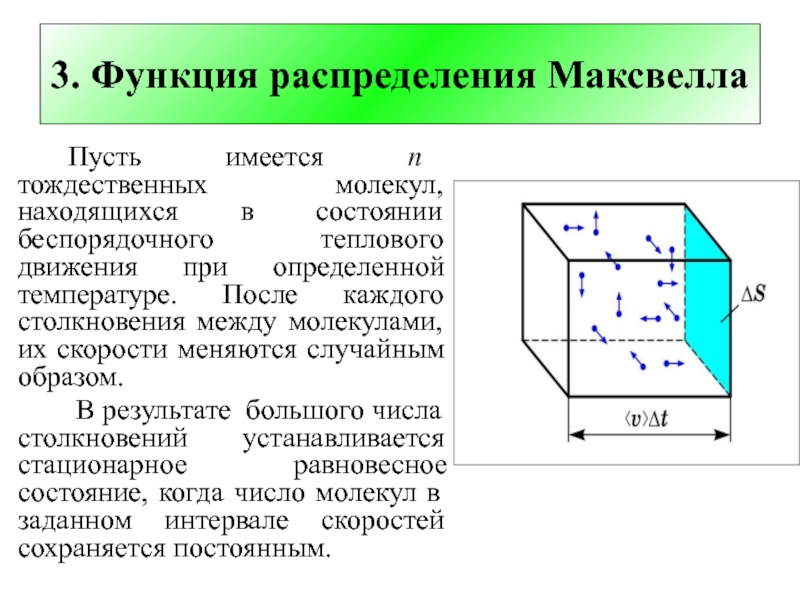
Слайд 263. Функция распределения Максвелла
Пусть имеется n тождественных молекул, находящихся
в состоянии беспорядочного теплового движения при определенной температуре. После каждого
столкновения между молекулами, их скорости меняются случайным образом.
В результате большого числа столкновений устанавливается стационарное равновесное состояние, когда число молекул в заданном интервале скоростей сохраняется постоянным.
Слайд 27 В результате каждого столкновения проекции скорости молекулы испытывают случайное изменение
на υx, υy, υz, причем изменения каждой проекции скорости независимы
друг от друга.
Найдем в этих условиях, каково число частиц dn из общего числа n имеет скорость в интервале
от υ до
Слайд 28 При этом, мы не можем ничего определенного сказать о точном
значении скорости той или иной частицы υi, поскольку за столкновениями
и движениями каждой из молекул невозможно проследить ни в опыте, ни в теории. Такая детальная информация вряд ли имела бы практическую ценность.
Распределение молекул идеального газа по скоростям впервые было получено знаменитым английским ученым Дж. Максвеллом в 1860 году с помощью методов теории вероятностей.
Слайд 29 Скорость – векторная величина. Для проекции скорости на ось х
(x-ой состав-ляющей скорости), имеем
тогда
или
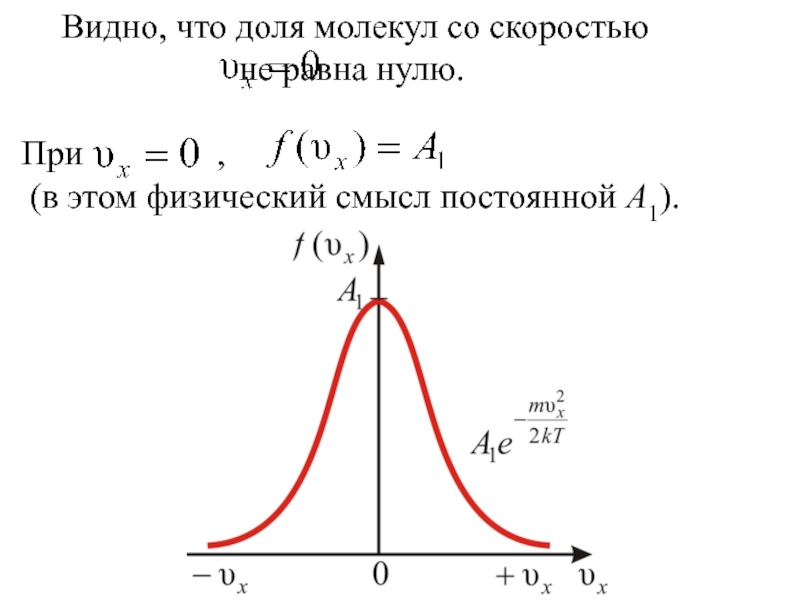
Слайд 30 Видно, что доля молекул со скоростью
не равна нулю.
При ,
(в этом физический смысл постоянной А1).
Слайд 31 Приведённое выражение и график справедливы для распределения молекул газа по
x-ым компонентам скорости. Очевидно, что и по y–ым и z–ым
компонентам скорости также можно получить:
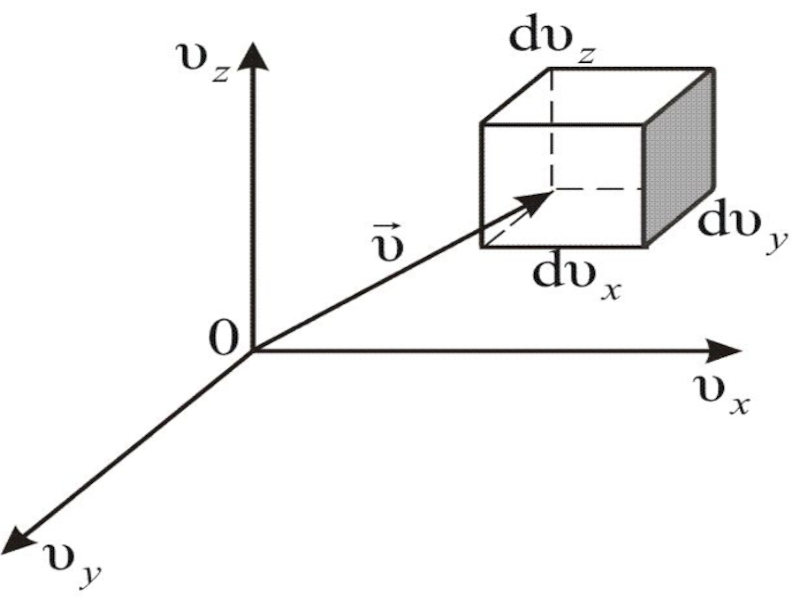
Слайд 32 Вероятность того, что скорость молекулы одновременно удовлетворяет трём
условиям: x – компонента скорости лежит в интервале от υх
до ; y – компонента, в интервале от υy до ; z – компонента, в интервале от υz до будет равна произведению вероятностей каждого из условий (событий) в отдельности:
где
(5)
Этой формуле можно дать геометрическое истолкование: dnxyz – это число молекул в параллелепипеде со сторонами dυx, dυy, dυz, то есть в объёме (рисунок 4), находящемся на расстоянии от начала координат в пространстве скоростей.
Слайд 35 закон Максвелла – распределение молекул по абсолютным значениям скоростей:
(6)
где – доля всех частиц единичного объёма, скорости которых лежат в интервале от υ до
Слайд 36 При получаем плотность вероятности,
или функцию распределения молекул по скоростям:
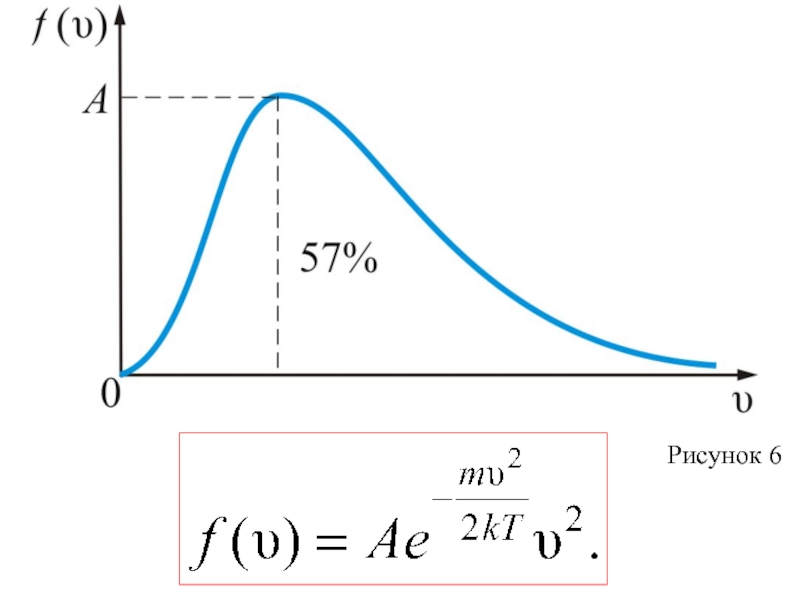
(7)
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.
тогда,
из (7) получим:
(8)
График этой функции показан на рис. 6.
Слайд 39Выводы:
- Вид распределения молекул газа по скоростям, для каждого
газа зависит от рода газа (m) и от параметра состояния
(Т). Давление P и объём газа V на распределение молекул не влияют.
- В показателе степени стоит отношение, кинетической энергии, соответствующей данной скорости υ к средней энергии теплового движения молекул при данной температуре:
Слайд 40 Значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии
(то есть показывает, какова вероятность при данной температуре иметь именно
такое значение кинетической энергии).
Слайд 414. Барометрическая формула
Рассмотрим ещё один, очень важный
закон.
Атмосферное давление на какой-либо высоте h обусловлено весом выше
лежащих слоёв газа.
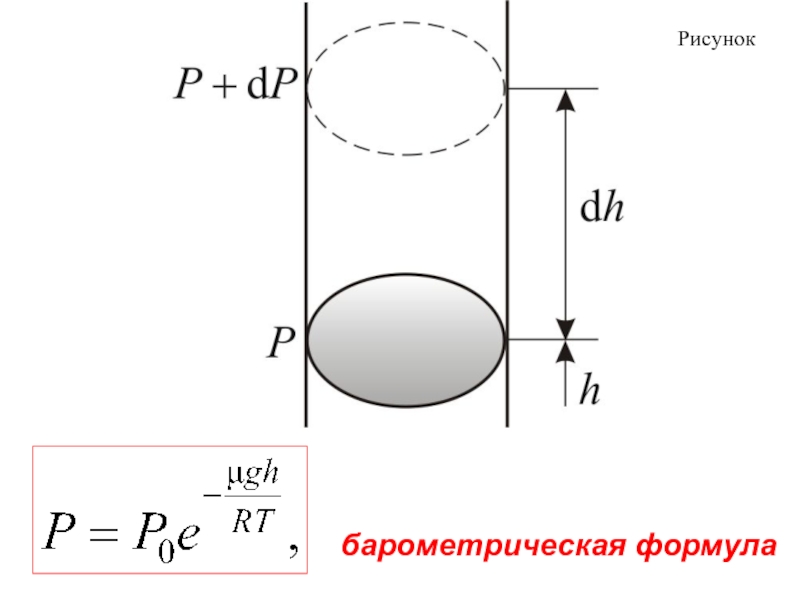
Пусть P – давление на высоте h, а – на высоте
(рисунок 10).
dР < 0, так как на большей высоте давление меньше.
Разность давления
равна весу газа, заключённого в объёме цилиндра с площадью основания равного единице и высотой dh, ρ плотность газа на высоте h, медленно убывает с высотой.
Отсюда
(12)
где P0 – давление на высоте . Это барометрическая формула.
Слайд 44 Из барометрической формулы следует, что P убывает с
высотой тем быстрее, чем тяжелее газ (чем больше μ) и
чем ниже температура (например, на больших высотах концентрация легких газов Не и Н2 гораздо больше чем у поверхности Земли).
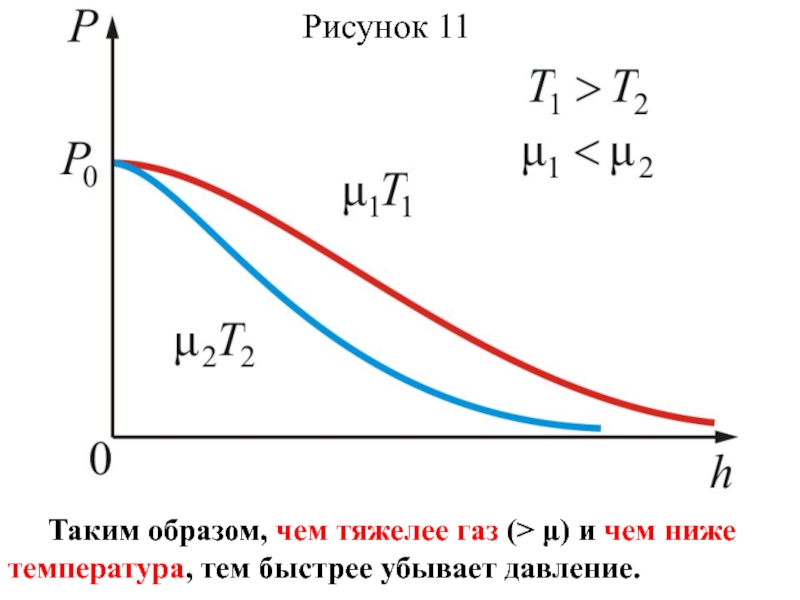
На рисунке 11 изображены две кривые, которые можно трактовать, либо как соответствующие разным μ (при одинаковой Т), либо как отвечающие разным Т, при одинаковых μ.
Слайд 45Рисунок 11
Таким образом, чем тяжелее газ (> μ) и чем
ниже температура, тем быстрее убывает давление.
Слайд 465. Распределение Больцмана
Распределение Больцмана определяет распределение частиц в
силовом поле в условиях теплового равновесия.
Слайд 47 Пусть идеальный газ находится в поле консервативных сил, в условиях
теплового равновесия. При этом, концентрация газа будет различной в точках
с различной потенциальной энергией, что необходимо для соблюдения условий механического равновесия.
Число молекул в единичном объеме n убывает с удалением от поверхности Земли, и давление, в силу соотношения
тоже убывает.
Слайд 48 Исходя из основного уравнения молекулярно-кинетической теории:
, заменим P и P0 в барометрической
формуле (12) на n и n0 и получим распределение Больцмана для молярной массы газа:
(13)
где n0 и n число молекул в единичном объёме на высоте h = 0 и h, соответственно.
, то распределение Больцмана можно представить в виде:
(14)
Слайд 50
С уменьшением температуры число молекул на высотах, отличных от нуля,
убывает. При
тепловое движение прекращается, все молекулы расположились бы на земной поверхности.
При высоких температурах, наоборот, молекулы оказываются распределёнными по высоте почти равномерно, а плотность молекул медленно убывает с высотой.
–потенциальная энергия, следовательно, распределение Больцмана характеризует распределение частиц
по значениям потенциальной энергии:
(15)
– это закон распределения частиц по потенциальным энергиям – распределение Больцмана. Здесь n0 – число молекул в единице объёма в там, где .
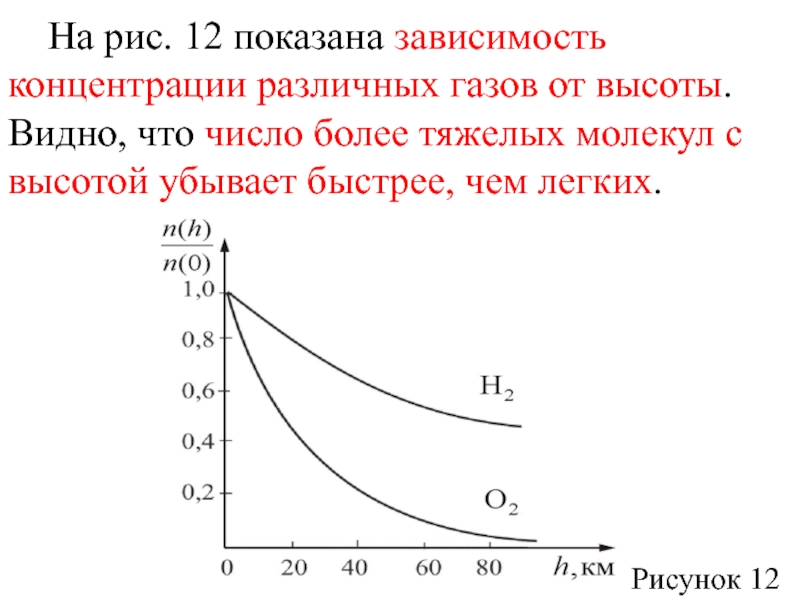
Слайд 52 На рис. 12 показана зависимость концентрации различных газов от высоты.
Видно, что число более тяжелых молекул с высотой убывает быстрее,
чем легких.
Рисунок 12
Слайд 536. Закон распределения Максвелла-Больцмана
В п. 3 мы получили
выражение для распределения молекул по скоростям (распределение Максвелла):
(17)
Слайд 54 Из этого выражения легко найти распределение молекул газа по значениям
кинетической энергии K. Для этого перейдём от переменной υ к
переменной :
где dn(K) – число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от K до
Слайд 55 Отсюда получим функцию распределения молекул по энергиям теплового
движения:
(18)
Средняя кинетическая энергия молекулы идеального газа:
то есть получили результат, совпадающий с прежним результатом, полученным в п. 3.
Слайд 56 Итак, закон Максвелла даёт распределение частиц по значениям
кинетической энергии а закон Больцмана – распределение частиц по значениям
потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла-Больцмана, согласно которому, число молекул в единице объёма, скорости которых лежат в пределах от υ до
равно:
(19)
– полная энергия. Тогда
(20)
Это и есть закон распределения Максвелла-Больцмана.
Здесь n0 – число молекул в единице объёма в той точке, где ;
.