Парадоксы теории относительности

и геометрических свойствах пространства, но, кажется, только еще больше его

запутала, создав некоего мутанта под названием

"Четырехмерное Пространство-Время".

Однако, при внимательном рассмотрении в ней обнаруживаются явные противоречия, на которые принято закрывать глаза. Считается чуть ли не «дурным тоном» говорить о парадоксах СТО.

ИСО с околосветовой скоростью, его время относительно B замедляется, и

по возвращении на Землю близнец A оказывается моложе близнеца B.

Но с точки зрения A, это B вместе с Землей движется относительно A, и это время B должно замедляться, т.е. B оказывается моложе A.

Данный парадокс объясняется тем, что система отсчета космонавта A не является инерциальной – он испытывает ускорения, что естественно делает ситуацию несимметричной.

Парадокс связан с формулой

T – интервал времени в движущейся системе отсчета, Тₒ - в неподвижной.

станции C одновременно с одинаковыми скоростями в противоположных направлениях,
пролетают одинаковое

расстояние и возвращаются на C. Кто из них окажется моложе?

Дабы избежать упреков в том, что системы отсчета космонавтов не являются находящихся на одинаковом расстоянии от C, не тормозят и не разворачиваются, а пошлют друг другу радиосообщение, в котором укажут свой возраст. Разумеется, на преодоление расстояния от одного корабля до другого радиосигналу потребуется некоторое время , и каждый космонавт получит сообщение от другого гораздо позже, чем отправит свое. Но в полученном A сообщении будет указан возраст B такой же, каким был возраст A, когда он отправлял свое сообщение, а в полученном B сообщении будет указан возраст A такой же, каким был возраст B в момент отправки его сообщения. Т.е. в обоих сообщениях будет указан одинаковый возраст.

скоростью V
На поезде, в его середине, находится импульсный излучатель

света O’, а в начале и конце – приемники излучения A и B, при этом AO’= O’B.

O

В момент, когда O’ поравнялся со стоящим на перроне вокзала наблюдателем O, излучатель испускает импульс света. В поезде, вследствие равенства расстояний AO’ и

и O’B, приемники A и B примут световые сигналы одновременно.

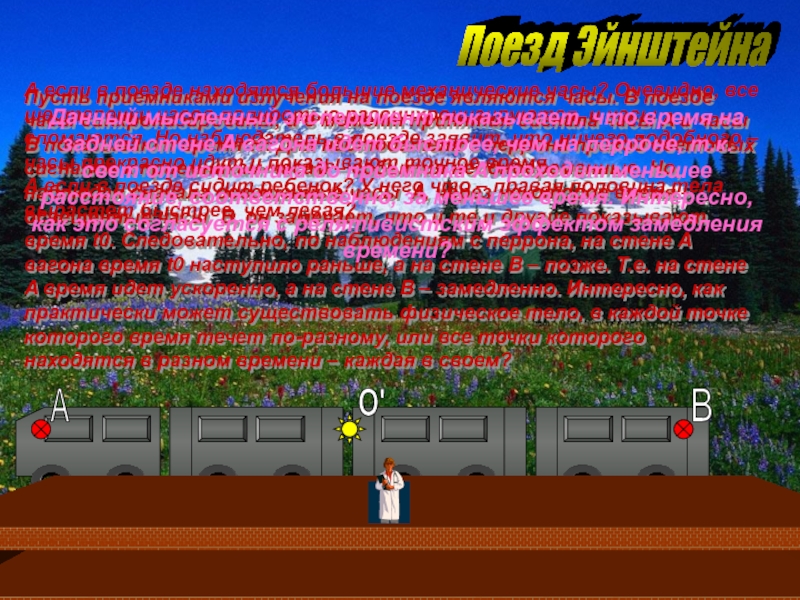
часы синхронизированы, и в момент принятия сигнала часы A и

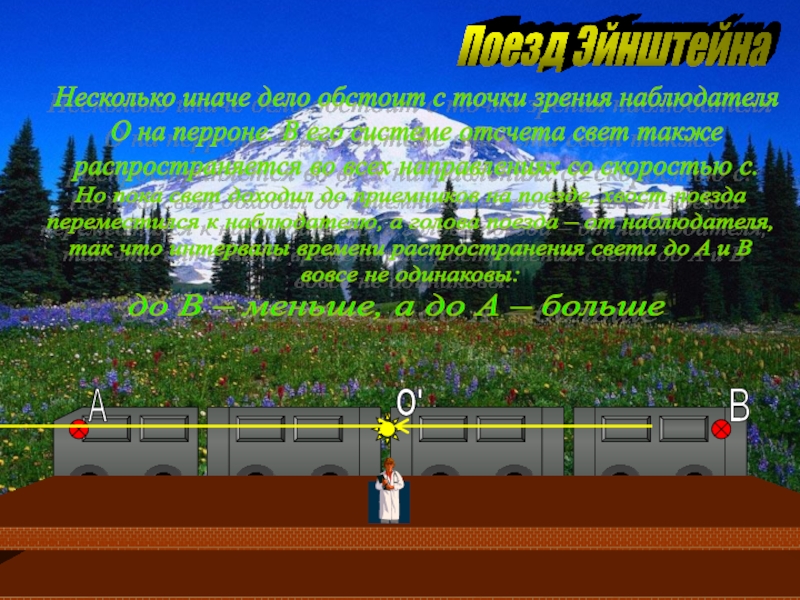
часы B показывают время t0. Для наблюдателя с перрона приход световых сигналов к приемникам-часам – события неодновременные. Но, наблюдая сначала освещенные часы  A, через некоторое время – освещенные часы  B, он замечает, что и те и другие показывают время t0. Следовательно, по наблюдениям с перрона, на стене A вагона время t0 наступило раньше, а на стене B – позже. Т.е. на стене A время идет ускоренно, а на стене B – замедленно. Интересно, как практически может существовать физическое тело, в каждой точке которого время течет по-разному, или все точки которого находятся в разном времени – каждая в своем?

А если в поезде находятся большие механические часы? Очевидно, все шестеренки часов полностью рассинхронизируются, и часы сломаются. Но наблюдатель в поезде заявит, что ничего подобного – часы прекрасно идут и показывают точное время.
А если в поезде сидит ребенок? У него что – правая половина тела вырастет быстрее, чем левая?

Данный мысленный эксперимент показывает, что время на задней стене A вагона идет быстрее, чем на перроне, т.к. свет от источника до приемника A проходит меньшее расстояние, соответственно, за меньшее время. Интересно, как это согласуется с релятивистским эффектом замедления времени?

именно то, что все точки движущейся целой структуры, основанной на

причинно-следственных

закономерностях, находятся в разном времени.

Инвариантность времени следует из инвариантности скорости света – следствие после причины наступает не раньше и не позже, а ровно через столько времени,

сколько требуется фундаментальному сигналу для прохождения расстояния от причины до следствия.

эффекта: если наблюдатель в S видит сокращение длины, то и

наблюдатель в S' должен видеть то же самое.

При правильном использовании, СТО не допускает никаких «парадоксов».

при скоростях, близких к скорости света, и , с другой

стороны, объясняет переход к классическим законам.

Специальная теория относительности А.Эйнштейна