Приращение функции и приращение аргумента

2)
2. Геометрический смысл приращения аргумента и приращения функции (слайд 3)

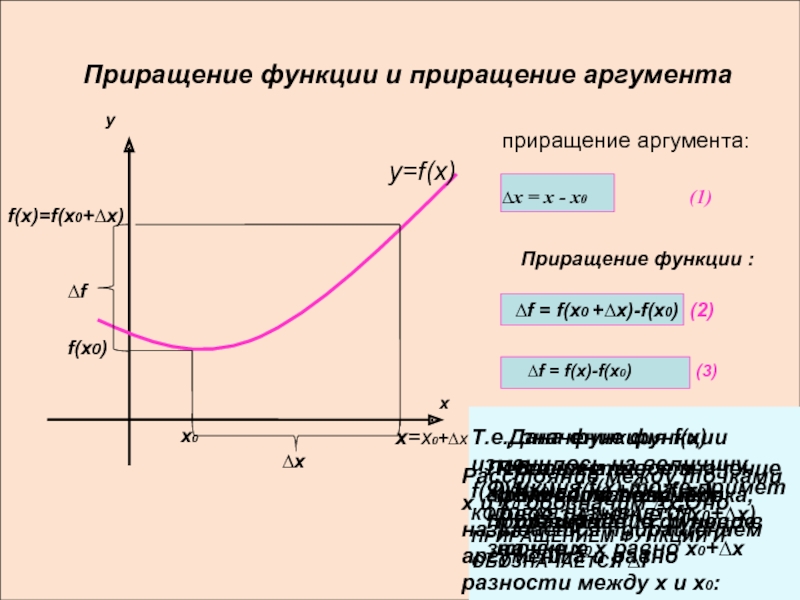
Приращение функции :

∆f = f(x0 +∆x)-f(x0) (2)

∆f = f(x)-f(x0) (3)

x

В окрестности точки х0 возьмём точку х

Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0

Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:

Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х

Функция f(х) тоже примет новое значение: f(x0+∆x)

Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f

Дана функция f(x)

x0

∆x

∆f

α

y = kx+b

k = tgα

α

∠α=∠MM0K

tg ∠ MMOK =

f(x0)

y

M0

К

=

Определим положение секущей

x

o

Геометрический смысл приращения аргумента и приращения функции

M

x

ОПРЕДЕЛИМ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРИРАЩЕНИЯ ФУНКЦИИ И ПРИРАЩЕНИЯ АРГУМЕНТА

Отметим на графике функции f(x) точки М0(х0; f(х0)) и М(х;f(х0 +Δх))

Координаты точки М можно рассматривать как приращение координат точки М0 Отметим эти приращения

Через точки М и М0 проведём прямую и запишем определение:

Определим положение секущей на координатной плоскости

Секущая-прямая. Положение прямой на плоскости задаёт её уравнение y = kx+b

Где k- тангенс угла, который прямая образует с положительным направлением оси ОХ

Отметим этот угол

Выполним дополнительные построения: через точку М0 проведём прямую, параллельную оси ОХ

Отметим точку К и рассмотрим прямоугольный (почему?) ∆ММ0К

∠α=∠MM0K ,как соответственные углы при секущей параллельных прямых

Выразим tg∠MM0K через приращение функции и приращение аргумента:

Вывод: угловой коэффициент секущей, проходящей через точки М0(х0; f(х0)) и М(х;f(х0+Δх)) равен отношению приращения функции к приращению аргумента (записать)