Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Введение в физику и моделирование фотонных кристаллов
Содержание
- 1. Введение в физику и моделирование фотонных кристаллов
- 2. Основные представленияЗонная структура фотонного кристалла - характеристика,
- 3. Основные представленияСобственная частота - другой важный термин,
- 4. Зонная структура 1-D фотонного кристаллаКаждый набор собственных
- 5. На рисунке горизонтальная ось соответствует волновому вектору
- 6. Если же частота излучения – ω2, то
- 7. Фактически, эти два рассмотренных случая содержат основные
- 8. ОСНОВНЫЕ ПРИНЦИПЫ ВОЛНОВОЙ ОПТИКИВзаимодействие между электромагнитным полем
- 9. Проблема взаимодействия электромагнитного поля, излучаемого точечным источником и оптической среды
- 10. Интервалы между атомами - один из ключевых
- 11. Фотон Фотон является электрически нейтральной частицей, т.
- 12. Слайд 12
- 13. Слайд 13
- 14. Предполагается:среда является однородной. оптическая среда изотропна и
- 15. Волновая оптикаЕсли ε, μ и σ материала
- 16. Геометрическая ОптикаЕсли размер объекта являются большим по
- 17. Представление оптического излучения в геометрической (a) и
- 18. Уравнения Максвелла распространения волн Свет состоит из электрического
- 19. В пределах классической теории все электромагнитные явления
- 20. Векторы E и H – координатно
- 21. Плотность заряда ρ и плотность тока J
- 22. Магнитные индукции связаны с полевыми векторами материальными
- 23. Реакция многих твердых тел к приложенному электрическому
- 24. Электромагнитные волны переносят энергию, поскольку они перемещаются
- 25. Волновое уравнение в вакуумеВ вакууме нет никаких
- 26. так какВекторные соотношения дают оператор ЛапласаВолновое уравнение
- 27. Решение волнового уравненияОбщая форма решения уравнения имеет
- 28. Волновой вектор – вектор, который определяет волновое
- 29. Физический смысл волнового решенияможно интерпретировать следующим образом.
- 30. Особый случай важен для понимания распространения волн
- 31. Если предполагать, что волновой фронт – линия
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Основные представления
Зонная структура фотонного кристалла - характеристика, которая дает большую
часть общей информации о свойствах фотонного кристалла.
собственных состояний или собственных частот бесконечной периодической структуры.Слайд 3Основные представления
Собственная частота - другой важный термин, ее также называют
резонансной частотой структуры. Так как фотонный кристалл - бесконечная периодическая
структура, то появляется много отражений Френеля на поверхностях раздела носителей.Усиление и ослабление за счет интерференции между прямыми и обратными волнами вызывает или прохождение, или отражение излучения.
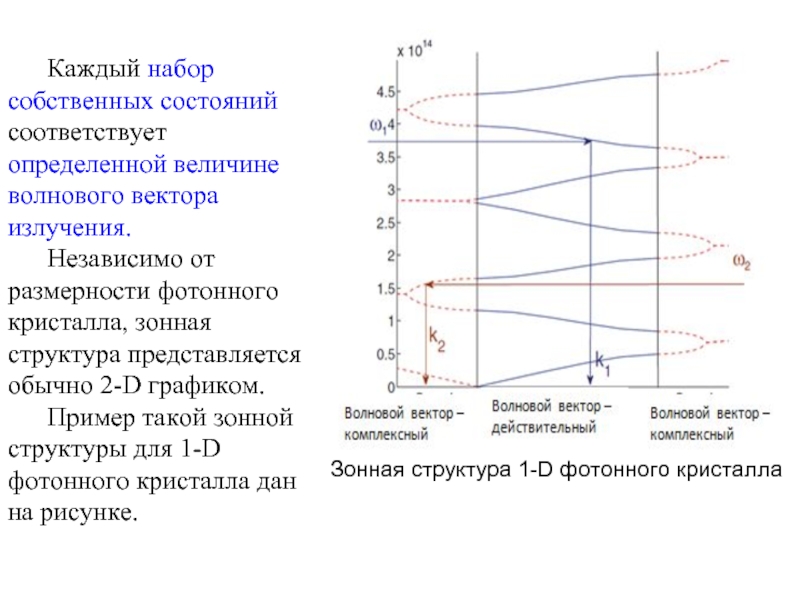
Слайд 4Зонная структура 1-D фотонного кристалла
Каждый набор собственных состояний соответствует определенной
величине волнового вектора излучения.
Независимо от размерности фотонного кристалла, зонная
структура представляется обычно 2-D графиком. Пример такой зонной структуры для 1-D фотонного кристалла дан на рисунке.
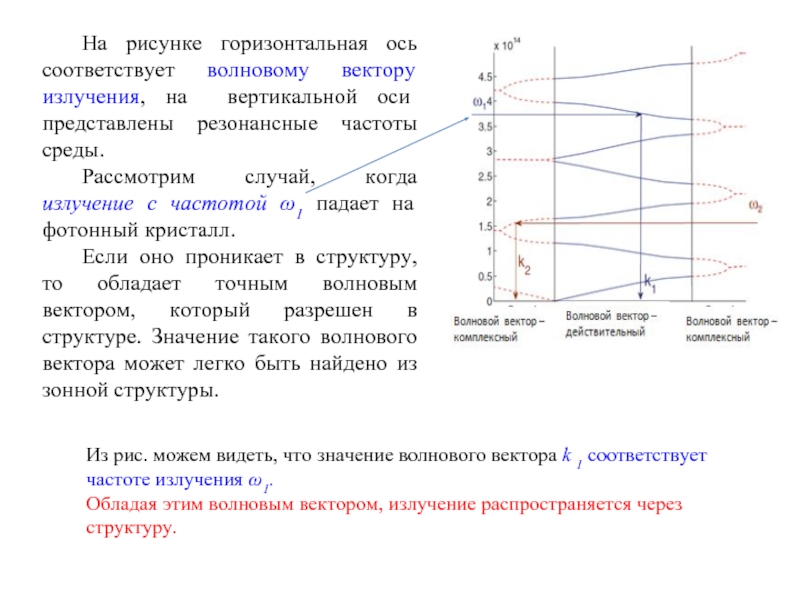
Слайд 5На рисунке горизонтальная ось соответствует волновому вектору излучения, на вертикальной
оси представлены резонансные частоты среды.
Рассмотрим случай, когда излучение с
частотой ω1 падает на фотонный кристалл. Если оно проникает в структуру, то обладает точным волновым вектором, который разрешен в структуре. Значение такого волнового вектора может легко быть найдено из зонной структуры.
Из рис. можем видеть, что значение волнового вектора k 1 соответствует частоте излучения ω1.
Обладая этим волновым вектором, излучение распространяется через структуру.
Слайд 6Если же частота излучения – ω2, то оно распространяется в
частотном диапазоне, для которого нет дозволенных реальных волновых векторов.
Известно,
что значение волнового вектора k2 может быть комплексным. Мнимая часть волнового вектора соответствует или затуханию излучения или усилению. В нашем случае это соответствует затуханию и означает, что излучение с частотой ω2 будет отражено от структуры. Однако, затухание имеет конечное значение, излучение проникнет в структуру на некоторое расстояние.
Слайд 7Фактически, эти два рассмотренных случая содержат основные принципы фотонного анализа
зонной структуры.
А именно, периодическая среда обладает разрешенными и запрещенными
частотными диапазонами. Излучение распространяется в структуре только в пределах разрешенных частот. Иначе, оно будет отражено.Слайд 8ОСНОВНЫЕ ПРИНЦИПЫ ВОЛНОВОЙ ОПТИКИ
Взаимодействие между электромагнитным полем и средой –
основной вопрос для понимания основных принципов оптического распространения волн в
волноводах и работе многих других пассивных и активных оптических устройств.Теоретические модели оптической среды
Обсуждение основных принципов волновой оптики должно состоять из следующих вопросов:
какова оптическая среда и какие свойства имеет среда;
как оптическая среда влияет на электромагнитное поле;
как описать электромагнитное поле и его взаимодействие с оптической средой
Слайд 9Проблема взаимодействия электромагнитного поля, излучаемого точечным источником и оптической среды
Слайд 10Интервалы между атомами - один из ключевых пунктов для исследования
взаимодействия со светом.
(электронная плотность)
В оптических устройствах и оптических структурах
толщина слоев в случае многослойной структуры или размера элементов в случае фотонных кристаллов может быть сопоставимой с длиной волны. В таком случае взаимодействие света со средой может иметь различные эффекты, такие как прозрачность, полное или частичное отражения и рефракция.
В оптических средах, используемых в технологии световых волн, интервал между атомами имеет порядок 1÷10Å, который является малой величиной по сравнению с длиной волны света, который используется в оптической связи (их длины волны находятся в диапазоне 0.8 ÷1.6 μм).
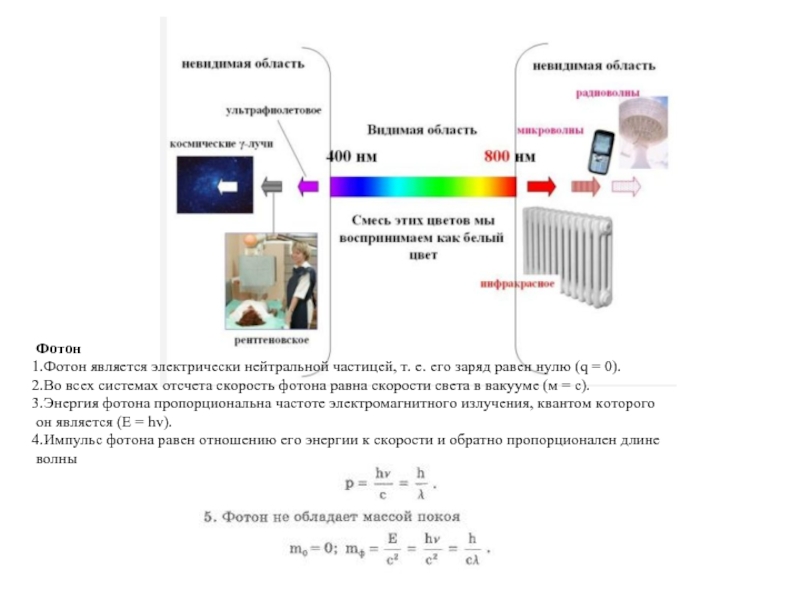
Слайд 11Фотон
Фотон является электрически нейтральной частицей, т. е. его заряд
равен нулю (q = 0).
Во всех системах отсчета скорость
фотона равна скорости света в вакууме (м = с). Энергия фотона пропорциональна частоте электромагнитного излучения, квантом которого он является (Е = hv).
Импульс фотона равен отношению его энергии к скорости и обратно пропорционален длине волны
Слайд 14Предполагается:
среда является однородной.
оптическая среда изотропна и независима от времени.
свойства
оптической среды описываются диэлектрической постоянной ε, проницаемостью μ и проводимостью
σ.В особых случаях у оптической среды возникает нелинейная реакция на внешнее влияние. Нелинейные эффекты, такие как генерация второй гармоники, эффект Керра, солитоны и формирование вихрей, и т.д., играют все более важную роль в усовершенствовании оптоэлектроники и фотоники.
Слайд 15Волновая оптика
Если ε, μ и σ материала определены, тогда решение
уравнений Максвелла является основой для анализа распространения света с точки
зрения волновой оптики. Волновая оптика обеспечивает решение задач распространения электромагнитных волн в световодах, а именно, определяя амплитуды электрических и магнитных составляющих оптического поля, а так же распределение его фаз и амплитуд в пространстве.Если толщина ядра световода имеет порядок длины волны, то распространение может быть описано с несколькими модами, которые являются функциями параметров световода и длины волны света.
Слайд 16Геометрическая Оптика
Если размер объекта являются большим по сравнению с длиной
волны света, то можно использоваться приближенный метод для изучения распространения
света.Геометрическая оптика или лучевая оптика используют методы геометрии, чтобы сформулировать законы оптики.
В геометрической оптике вводится понятие световых лучей, чтобы описать оптические явления. Пути распространения световых лучей в неоднородных и составных средах, выведены из так называемого уравнения эйконала.
Уравнение эйконала (др.-греч. (др.-греч. εἰκών) — это нелинейное дифференциальное уравнение в частных производных (др.-греч. εἰκών) — это нелинейное дифференциальное уравнение в частных производных, встречающееся в задачах распространения волн, когда волновое уравнение аппроксимируется с помощью теории ВКБ (др.-греч. εἰκών) — это нелинейное дифференциальное уравнение в частных производных, встречающееся в задачах распространения волн, когда волновое уравнение аппроксимируется с помощью теории ВКБ. Оно является следствием уравнений Максвелла (др.-греч. εἰκών) — это нелинейное дифференциальное уравнение в частных производных, встречающееся в задачах распространения волн, когда волновое уравнение аппроксимируется с помощью теории ВКБ. Оно является следствием уравнений Максвелла, и связывает волновую оптику (др.-греч. εἰκών) — это нелинейное дифференциальное уравнение в частных производных, встречающееся в задачах распространения волн, когда волновое уравнение аппроксимируется с помощью теории ВКБ. Оно является следствием уравнений Максвелла, и связывает волновую оптику с геометрической оптикой. Уравнение эйконала может быть представлено в форме:
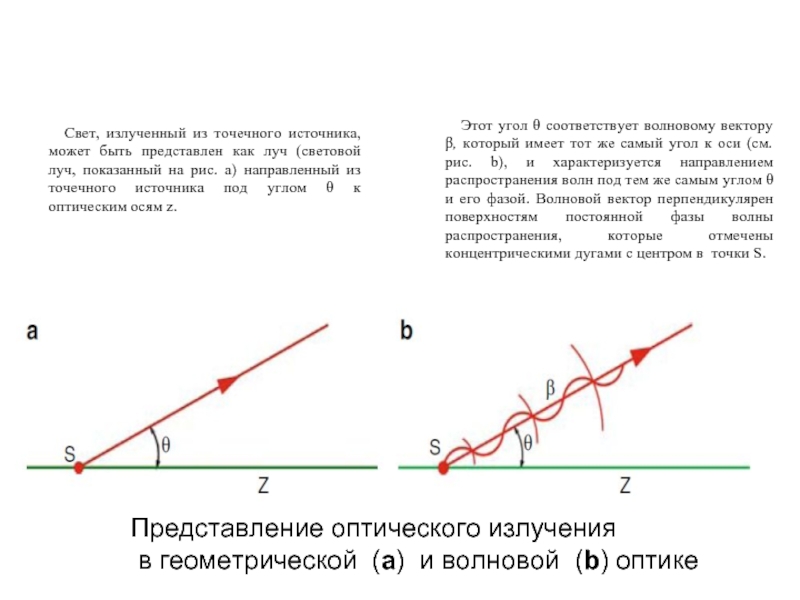
Слайд 17Представление оптического излучения
в геометрической (a) и волновой (b) оптике
Свет,
излученный из точечного источника, может быть представлен как луч (световой
луч, показанный на рис. a) направленный из точечного источника под углом θ к оптическим осям z.
Этот угол θ соответствует волновому вектору β, который имеет тот же самый угол к оси (см. рис. b), и характеризуется направлением распространения волн под тем же самым углом θ и его фазой. Волновой вектор перпендикулярен поверхностям постоянной фазы волны распространения, которые отмечены концентрическими дугами с центром в точки S.
Слайд 18Уравнения Максвелла распространения волн
Свет состоит из электрического поля и магнитного
поля, которые колеблются с очень высокой частотой, порядка 1014 Гц.
Распространение этого поля описывается периодическими функциями.Распространение энергии электромагнитной волны через вакуум реализуется электрическими и магнитными полями, которые обмениваются энергией, удовлетворяющей условиям Ампера и законам Фарадея. Изменения магнитного поля перпендикулярны электрическому полю.
Одночастотная электромагнитная волна создает гармонические колебания электрических и магнитных полей в пространстве. В любой фиксированной точке пространства амплитуда поля меняется с оптической частотой. Величина поля повторяет себя после одного периода колебания.
Волна повторяет себя в пространстве на интервале λ, называемым длиной волны, которая является фактически пространственным периодом волны. Обратная величина называется волновым числом.
Слайд 19 В пределах классической теории все электромагнитные явления описываются системой уравнений
Максвелла, которая дает временную зависимость электрических и магнитных полей и
их взаимодействия с оптической средой.Прежде, чем обсудить распространение света в сложных оптических структурах, таких как фотонные кристаллы, рассмотрим его распространение в свободном пространстве.
Для носителя со свободными зарядами и с током, уравнения Максвелла имеют следующую форму
Слайд 20
Векторы E и H – координатно зависящие от времени
векторы электрических и магнитных полей, соответственно.
D и B -
диэлектрическое смещение и магнитная индуктивность. Источники электромагнитного поля - плотность заряда ρ и плотность тока J.
Слайд 21Плотность заряда ρ и плотность тока J соединены уравнением непрерывности,
которое получается, если взять дивергенцию от уравнения (*), использовать (**)
и соотношениеВ случае непроводящей среды, такой как кварц или другой материал, используемый для распространения оптических волн в пассивных устройствах (оптическое волокно или планарный волновод), J = 0 и ρ = 0.
Слайд 22Магнитные индукции связаны с полевыми векторами материальными соотношениями
Электрическая и магнитная
константы
P – электрическая поляризация среды, вызванная электрическим полем E в
среде;М – магнитная поляризация среды.
Для оптических волокон М = 0 из-за немагнитной природы кварцевого стекла.
Произведение констант ε0 и μ0 равно
c = 3 · 108 м/с
Слайд 23Реакция многих твердых тел к приложенному электрическому полю такова, что
электрическое поле в образце меньше, чем внешнее приложенное. Это подобно
твердому телу, которое создало свое собственное распределение заряда, то есть, оно становится поляризованным, так, чтобы оно создало электрическое поле, которое направлено против внешнего поля. Материалы, которые обладают такими свойствами, вызывают диэлектриками.В однородной линейной и изотропной диэлектрической среде, которая рассматривается здесь, поляризация устанавливается обратно пропорционально направлению электрического поля E. В анизотропном материале поляризация и поле находятся не обязательно в том же самом направлении. Вообще, соотношение между E и P могут быть нелинейным. Хотя нелинейные эффекты в световодах заслуживают отдельного рассмотрения, они могут игнорироваться при описании оптоволоконных мод.
Слайд 24Электромагнитные волны переносят энергию, поскольку они перемещаются через вакуум. Существует
плотность энергии, связанная и с электрическими и магнитными полями. Количество
энергии переносимой через единицу площади описывается векторомВектор S вызывается вектором Пойнтинга.
Учитывая, что он выражается через векторное произведение магнитного и электрического полей, которые взаимно перпендикулярны, то S будет перпендикулярен плоскостям E, B и совпадать с направлением распространения волн.
Слайд 25Волновое уравнение в вакууме
В вакууме нет никаких носителей. В результате
нет никакой наведенной поляризации или тока. Другими словами, P и
J равны нулю. Поэтому, уравнения Максвелла приобретают видЭти четыре уравнения описывают взаимозависимость между E и H. Чтобы решить систему уравнений, можно выделить H и вывести уравнение только для E.
Взяв ротор от первого уравнения и используя материальные уравнения
получим
Слайд 26
так как
Векторные соотношения дают
оператор Лапласа
Волновое уравнение для электрического поля
в вакууме
Подобное волновое уравнение может быть получено для магнитной составляющей
H, избавляясь E.Слайд 27Решение волнового уравнения
Общая форма решения уравнения имеет форму:
где r =
(x, y, z) является координатным вектором,
k = (kx, ky,
kz) является волновым вектором, ω =2π/λ - угловая частота, а λ - длина волны.
Функции E+и E- описывают поведение волны в пространстве (аргумент k·r) и времени (аргумент ωt),
a+ и a- - амплитудные коэффициенты, зависящие от граничных условий.
Слайд 28Волновой вектор – вектор, который определяет волновое число и направление
распространения волны.
Модуль волнового вектора указывает волновое число.
Ориентация волнового
вектора указывает направление распространения волн. Волновое число указывает число колебаний электрических и магнитных векторов на единицу пространства и измерено в м-1.
Компоненты волнового вектора соответствуют волновым числам в x, y и z направлениях следующим образом:
Слайд 29Физический смысл волнового решения
можно интерпретировать следующим образом.
Во-первых, пусть рассматривается
особый случай, когда kя = ky = 0.
В этом
случае параметр (k·r -ωt) сводится к:Это означает, что волна E+ является волной, распространяющейся в положительном k направлении со скоростью ω/kx.
Точно так же E- представляет волну, распространяющуюся в отрицательном k направлении.
В общем случае, когда все компоненты волнового вектора являются ненулевыми, волна распространяет в k направления со скоростью света.
Слайд 30Особый случай важен для понимания распространения волн и для практического
применения в решении для волнового уравнения в случае, когда у
поля есть только один компонент.Это решение вызывают плоской волной. Этот случай описывается как
Здесь, электрическое поле имеет только один компонент в x-направлении и распространяется в направлении по оси Z.
Здесь, электрическое поле имеет только один компонент в x-направлении и распространяется в направлении по оси Z.
На рис. показана синусоидальная плоская волна в пространстве двух размерностей. Большая стрелка - волновой вектор, который определяет направление распространения волны, его ориентация перпендикулярна к волновому фронту.
Как и в случае сферической волны, волновые фронты плоской волны - поверхности постоянной фазы. В данном случае - плоскости, разделенные одной длиной волны. Время развития волны определяется аргументом (ωt).
Z
Слайд 31Если предполагать, что волновой фронт – линия вдоль гребенки волны,
то волновые фронты – линии или поверхности постоянной фазы, и
уравнение, определяющее волновой фронт, является просто k •r = константа.Для одномерного распространения света только вдоль оси X мы получаем скалярное волновое число
Подставляя решение для электрического поля
в и интегрируя по времени, получим:
Электрическое поле и магнитные поля перпендикулярны направлению распространения волны.