Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Эффективные алгоритмы численного решения уравнений, систем, расчета производных, интегралов в Scilab
Содержание
- 1. Эффективные алгоритмы численного решения уравнений, систем, расчета производных, интегралов в Scilab
- 2. Scilab - это математическая система для выполнения
- 3. Пакет поддерживает основные элементарные и множество специальных
- 4. Особенностью пакета является то, что он предназначен
- 5. Scilab – это система компьютерной математики, которая
- 6. Кроме того, Scilab предоставляет широкие возможности
- 7. Решение уравнений Для формирования полиномов используется функция
- 8. Приведен более короткий вариант реализации того
- 9. Слайд 9
- 10. Решение систем линейных уравнений Прежде чем приступить
- 11. Общий вид K:K=Для решаемой системы:K=Общий вид k: k=Для решаемой системы:
- 12. Слайд 12
- 13. Интегрирование в Scilab Вычислить определенный интеграл в
- 14. Слайд 14
- 15. Вычисление производной в Scilab В Scilab можно
- 16. Слайд 16
- 17. Скачать презентанцию
Scilab - это математическая система для выполнения технических (числовых) расчетов, которая по характеру работы и принципам архитектуры схожа с известной математической системой MATLAB. Основным элементом данных в системе является массив, то
Слайды и текст этой презентации
Слайд 1Эффективные алгоритмы численного решения уравнений, систем, расчета производных, интегралов в
Scilab
Слайд 2Scilab - это математическая система для выполнения технических (числовых) расчетов,
которая по характеру работы и принципам архитектуры схожа с известной
математической системой MATLAB. Основным элементом данных в системе является массив, то есть система с самого начала ориентирована именно на работу с данными в табличном виде.Слайд 3Пакет поддерживает основные элементарные и множество специальных функций, применяемых в
математике. Scilab содержит также мощный набор средств для работы с
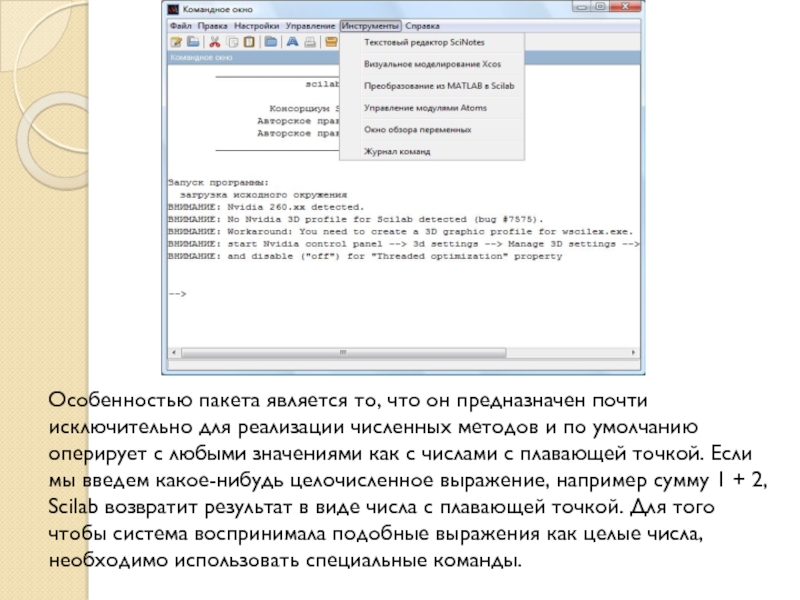
полиномами - как обычными, так и матричными. Например, имеются операторы для создания полинома с заданными корнями или коэффициентами, вычисления корней полинома (до сотой степени), деления двух полиномов, нахождения наибольшего общего делителя и наименьшего общего кратного нескольких полиномов и выполнения десятков других важных операций над полиномами.Слайд 4Особенностью пакета является то, что он предназначен почти исключительно для
реализации численных методов и по умолчанию оперирует с любыми значениями
как с числами с плавающей точкой. Если мы введем какое-нибудь целочисленное выражение, например сумму 1 + 2, Scilab возвратит результат в виде числа с плавающей точкой. Для того чтобы система воспринимала подобные выражения как целые числа, необходимо использовать специальные команды.Слайд 5Scilab – это система компьютерной математики, которая предназначена для выполнения
инженерных и научных вычислений, таких как:
решение нелинейных уравнений и систем;
решение
задач линейной алгебры;решение задач оптимизации;
дифференцирование и интегрирование;
задачи обработка экспериментальных данных (интерполяция и аппроксимация, метод наименьших квадратов);
решение обыкновенных дифференциальных уравнений и систем.
Слайд 6 Кроме того, Scilab предоставляет широкие возможности по созданию и
редактированию различных видов графиков и поверхностей.
Не смотря на то,
что система Scilab содержит достаточное количество встроенных команд, операторов и функций, отличительная ее черта это гибкость. Пользователь может создать любую новую команду или функцию, а затем использовать ее наравне со встроенными. К тому же, система имеет достаточно мощный собственный язык программирования высокого уровня, что говорит о возможности решения новых задач.
Слайд 7Решение уравнений
Для формирования полиномов используется функция poly. Так, для описания
из нашего примера обращение к функции poly будет выглядеть следующим
образом: g=poly ([-8, 0, 0, 1],'x','c').Последний этап вычисления корней уравнения состоит в вызове встроенной функции Scilab c именем roots (корни, англ.):
res=roots(g).
Слайд 8
Приведен более короткий вариант реализации того же алгоритма, но теперь
уже применительно к решению квадратного уравнения:
roots ( poly ([-2,-1,1],'x','c')).
Задание
для Scilab выглядит аналогично:roots(poly([12, 0, -13, 0, 1],'x','c')).
Слайд 10Решение систем линейных уравнений
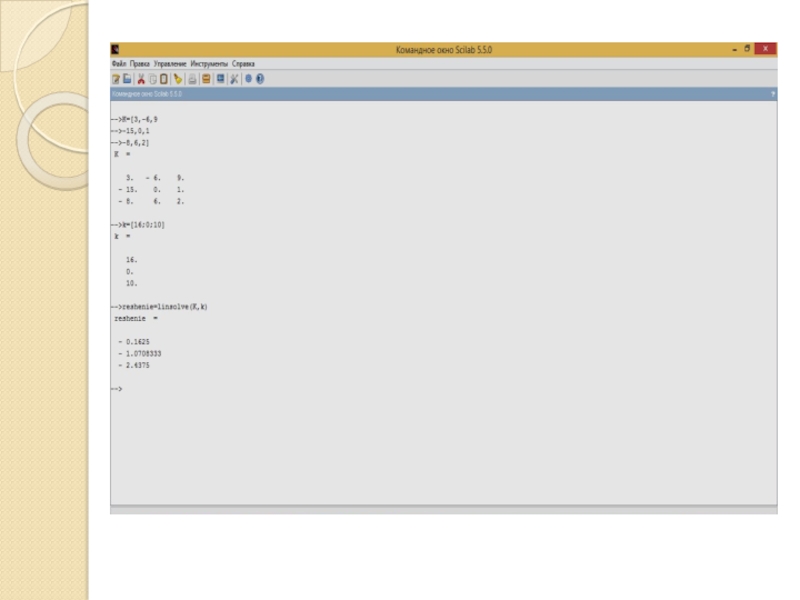
Прежде чем приступить к формированию задачи для
Scilab, необходимо привести систему уравнений к виду
Для нашего примера система
будет выглядеть следующим образом:Для решения подобных систем уравнений в Scilab существует функция linsolve. Обращение к ней выглядит следующим образом:
linesolve(K,k).
Слайд 13Интегрирование в Scilab
Вычислить определенный интеграл в Scilab можно при помощи
функции int (a, b, f), где а и b —нижний
и верхний пределы интегрирования соответственно, f — имя подынтегральной функции.Рассмотрим использование функции int на примере вычисления определенного интеграла:
В данном примере
Слайд 15Вычисление производной в Scilab
В Scilab можно вычислять производную функции в
заданной точке. Вычисление происходит при помощи команды numdiff(f,x0), где f
— имя дифференцируемой функции переменной х, x0 — координата точки в которой необходимо вычислить производную. Рассмотрим пример применения команды numdiff.Вычислим производную функции: