Криптосистемы с открытым ключем

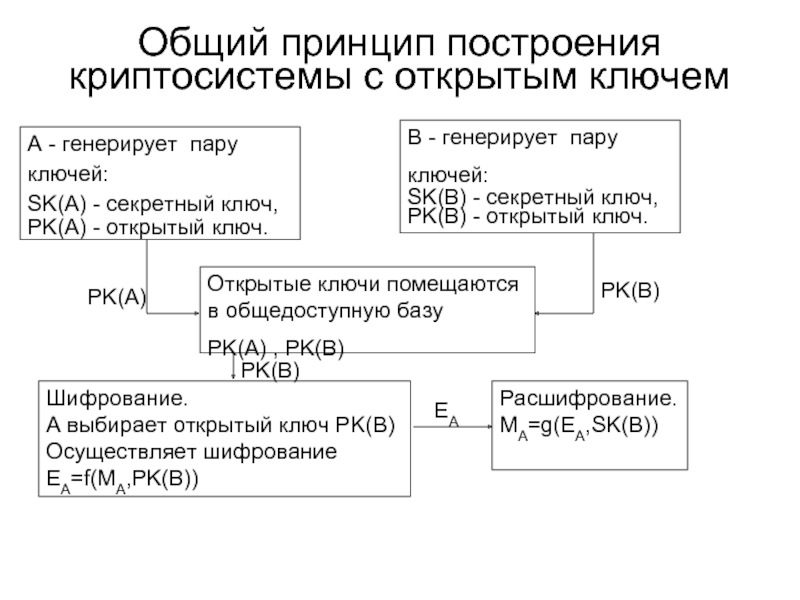
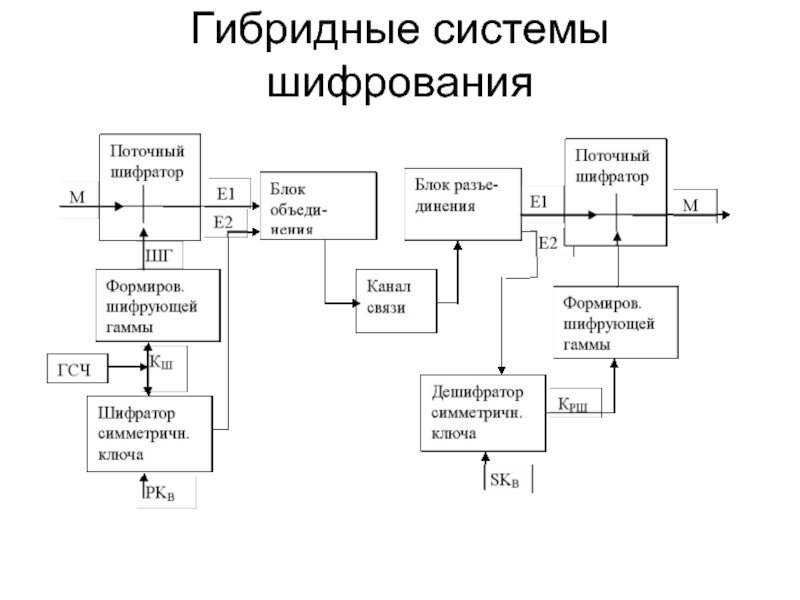
У. Диффи асимметричных криптографических систем;
1978

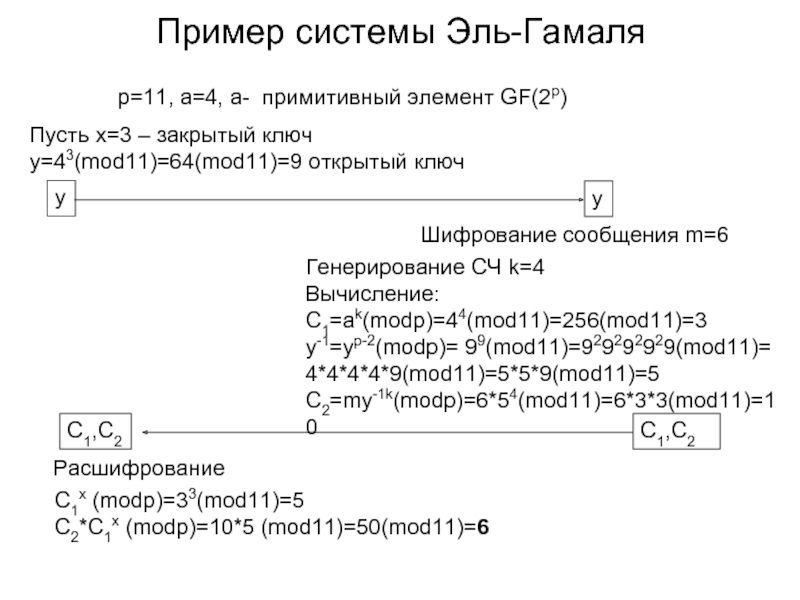
г. – Р. Райвест, А. Шамир, Л. Адельман – предложили первую систему ЭЦП, основанную на задаче факторизации большого числа;
1985 г. – Эль Гамаль предложил систему ЭЦП, основанную на задаче логарифмирования в поле чисел из р элементов;
1991 г.- Международный стандарт ЭЦП ISO/IEC 9796 (вариант РША);
1994 г. – Стандарт США FIPS 186 (вариант подписи Эль Гамаля);
1994 г. – ГОСТ Р 34.10-95 (вариант подписи Эль Гамаля);
2000 г. – Стандарт США FIPS 186 – 2;
2001 г. – ГОСТ Р 34.10-01 (ЭЦП на основе математического аппарата эллиптических кривых).

X , y ∈ Y называется односторонней (однонаправленной),
если y легко

вычисляется по любому x, а обратная функция x=f-1(y) является трудно вычислимой.

Пример ОФ.
y=ax(modp), где p- простое число, x - целое число,
a -примитивный элемент поля Галуа GF(p). То есть a такое число, что все его степени ai(modp), i= 1,2…p-1,
принимают все значения в множестве чисел от 1 до p-1.

примитивный элемент -
a1 =3(mod7), a2 =2(mod7), a3 =6(mod7), a4

=4(mod7), a5 =5(mod7), a6 =1(mod7).
Если x=4, то y=34(mod7)=4.

Сложность нахождения функции возведения в степень Nв=O(2logp).
Обратная функция x=logay (функция дискретного логарифмирования) трудно вычислима.
Если p - сильно простое число, то Nлог=O((p)1/2).

1000 разрядное двоичное число,

тогда для решения задачи возведения в степень числа х по modp потребуется примерно 2000 = 2*103 операций , а для нахождения логарифма такого числа потребуется примерно
p1/2=2500~10170 операций, что вычислительно невозможно осуществить ни за какое реально обозримое время.

невозможно, она содержит потайной ход (trapdoor), который позволяет вычислять обратную

функцию, если известен секретный параметр - ключ.

y=f(x,s) – легковычислима;
x=f-1(y) – трудновычислима;
x= f-1(y,s)- легковычислима.

- секретный ключ,
PK(A) - открытый ключ.
B - генерирует пару
ключей:
SK(B) -

секретный ключ,
PK(B) - открытый ключ.

Открытые ключи помещаются
в общедоступную базу
PK(A) , PK(B)

Шифрование.
А выбирает открытый ключ PK(B)
Осуществляет шифрование
EA=f(MA,PK(B))

Расшифрование.
MA=g(EA,SK(B))

EA

PK(A)

PK(B)

PK(B)

SK должно быть просто
решаемой задачей;
2. При известном ключе шифрования

PK вычисление криптограммы
E=f(M,PK) должно быть простым;
3. При известном ключе расшифрования SK восстанавливает сообщение
M=g(E,SK) должно быть простым;
4. При известном ключе шифрования PK вычисление ключа
расшифрования SK должно быть сложным;
5. При известном ключе шифрования PK, но неизвестном ключе
расшифрования SK вычисление М по известной криптограмме E
должно быть весьма сложным.

пары открытых ключей
A - генерирует число xA, вычисляет открытый ключ
yA=ax

(modp). (SK= xA , PK= yA).

yA передается корр. B.

Шифрование сообщения
Пусть корр. B хочет послать корр.А сообщение mГенерирует случайное число kФормирует криптограмму E=(c1c2)
c1=ak(modp), c2=m⋅(yA-1)k .
Отправляет E корр. А.

Корреспондент А

Корреспондент В

,
Затем находит
c2akx (modp)= m⋅(yA-1)k akx (modp)= m⋅a-xk akx (modp)=m

Замечание.
Как найти

yA-1 ?

yAp-2 (modp)= yAp-1 (modp) ⋅ yA-1 (modp) = yA-1 (modp)

логарифмирования.
2. Нахождение m без знания ключа возможно, если случайное число

k используется дважды и в одном случае нарушитель знает
открытый текст
c2= m⋅(yA-1)k (modp), c’2= m’⋅(yA-1)k (modp)
Зная c2, c’2 и m несложно найти m’ m’= c’2⋅m⋅c-12 (modp)

k должно меняться случайным образом при шифровании
нового сообщения.

закрытый ключ
y=43(mod11)=64(mod11)=9 открытый ключ
Шифрование сообщения m=6
Генерирование СЧ k=4
Вычисление:
С1=ak(modp)=44(mod11)=256(mod11)=3
y-1=yp-2(modp)= 99(mod11)=929292929(mod11)=
4*4*4*4*9(mod11)=5*5*9(mod11)=5
C2=my-1k(modp)=6*54(mod11)=6*3*3(mod11)=10
C1,C2
C1,C2
Расшифрование
C1x (modp)=33(mod11)=5
C2*C1x

(modp)=10*5 (mod11)=50(mod11)=6

q. Находится
модуль N=pq. Находится функция Эйлера ϕ(N)= (p-1)(q-1).
Выбираем число

e такое, что НОД(e, ϕ(N))=1.
Находим d, как обратный элемент к e, de=1(mod ϕ(N)).
Объявляем d=SK, (e,N)=PK. PK сообщается всем
корреспондентам.

Шифрование.
Корр. А передает зашифрованное сообщение корр.В
(использует открытый ключ корр. В)
E=me(modN)

Расшифрование.
Корр. В расшифровывает принятую криптограмму от
корр.А,используя свой секретный ключ.
m=Ed(modN)

т. Эйлера mϕ(N)≡1(modN) для любого m взаимно простого с

N.
Умножая обе части сравнения на m, получаем сравнение
mϕ(N)+1≡ m(modN) справедливое уже для любого целого m.
Перепишем соотношение ed≡1(modϕ(N)) в виде ed=1+kϕ(N)
для некоторого целого k.
Тогда Ed=(me)d=m1+kϕ(N)= m1+ϕ(N) m(k-1)ϕ(N)=
=m ⋅m(k-1)ϕ(N)= m1+(k-1)ϕ(N) =m1+ϕ(N) m(k-2)ϕ(N)=
…. = m1+ϕ(N) =m
Что и требовалось доказать.

m=6 E=me(modN)= 67(mod33)=62 62 62 61(mod33)=
=3*3*3*3*2=30
Расшифрование
Ed(modN)=303(mod33)=900*30(mod33)=9*30(mod33)=6

q по известному модулю N. Задача
факторизации имеет сложность O((N)1/2).
2.

Будем последовательно возводить полученную криптограмму в
степень равную значению открытого ключа т.е. (((((Ee)e)…..)e .
Если при некотором шаге окажется, что Ei=E , то это означает,
что Ei-1=m. Доказывается, что данная атака требует непереборно
большого числа шагов.
3. Поиск слабых ключей, для которых me’ = m , т.е. возведение
в степень не меняет сообщения. Эта атака имеет малую вероятность
успеха, если p и q выбираются среди сильно простых чисел. Сильно
простое число, это число, для которого p-1 не содержит в разложении
маленьких сомножителей, и имеет в разложении хотя бы один
большой сомножитель.
4.