Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Линейное уравнение с одной переменной — Математические модели
Содержание
- 1. Линейное уравнение с одной переменной — Математические модели
- 2. Научиться можно Только тому,Что любишьИоганн гёте
- 3. Правила «Космических гонок»
- 4. 1 этап Найдите число, противоположное корню уравнения
- 5. Ответ(2 + 3х) – (4х – 7)
- 6. Укажите сколько корней имеет каждое из уравнений.-
- 7. 3 этапРешите уравнение:
- 8. Ответ5(х + 9) – 3х = 155х
- 9. Во время соревнований из пункта
- 10. 5х + 5(х + 2) = 1605х
- 11. Моторная лодка за 2 ч по течению
- 12. 2(х + 3) = 3(х – 3)2х
- 13. Скачать презентанцию
Научиться можно Только тому,Что любишьИоганн гёте
Слайды и текст этой презентации
Слайд 1Интегрированный урок по темам
«Линейное уравнение с одной переменной. Математические
модели.»
Слайд 5Ответ
(2 + 3х) – (4х – 7) = 10
2 +
3х – 4х + 7 = 10
3х – 4х =
10 – 2 – 7х = 1
х = - 1
Число, противоположное корню: 1
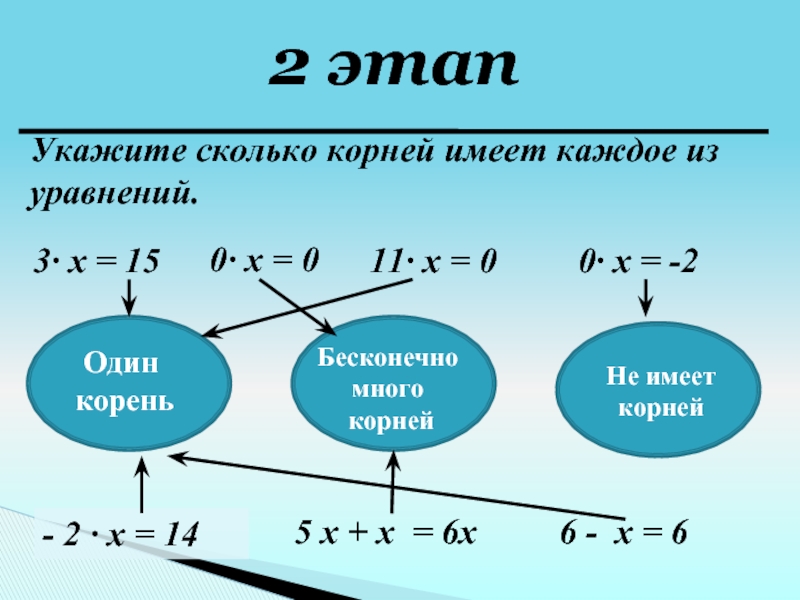
Слайд 6Укажите сколько корней имеет каждое из уравнений.
- 2 ∙ x
= 14
0∙ x = 0
11∙ x = 0
0∙ x
= -2Один
корень
Бесконечно много
корней
Не имеет корней
5 x + х = 6х
3∙ x = 15
6 - x = 6
2 этап
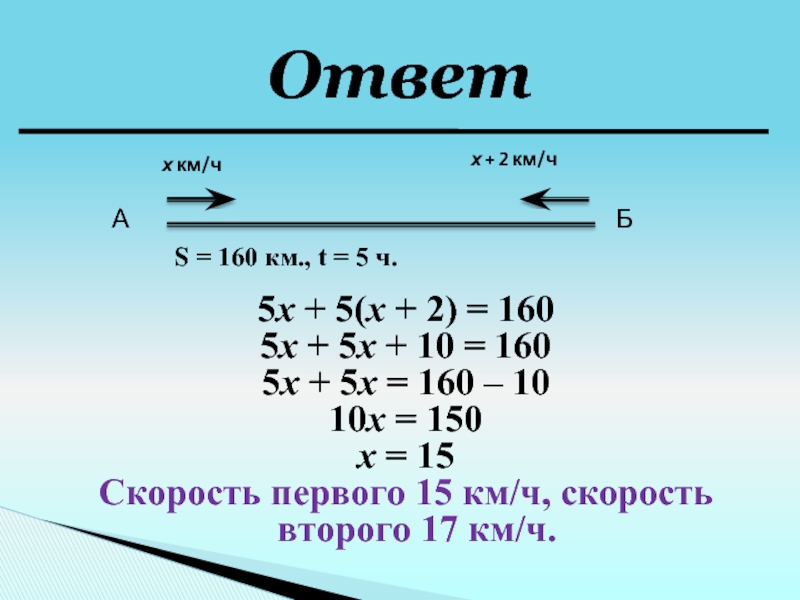
Слайд 9 Во время соревнований из пункта А и пункта
Б навстречу друг другу выехали 2 велосипедиста. Скорость одного из
них на 2 км/ч больше, чем скорость второго. Найти скорость каждого велосипедиста, если расстояние между пунктами 160 км, а встретились они через 5 часов.4 этап
Слайд 105х + 5(х + 2) = 160
5х + 5х +
10 = 160
5х + 5х = 160 – 10
10х =
150х = 15
Скорость первого 15 км/ч, скорость второго 17 км/ч.
Ответ
А
Б
х км/ч
х + 2 км/ч
S = 160 км., t = 5 ч.
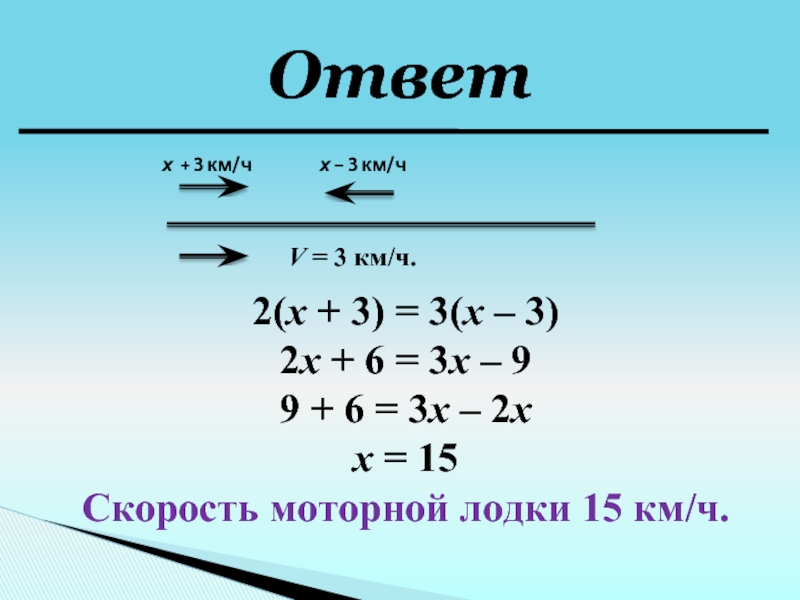
Слайд 11Моторная лодка за 2 ч по течению реки проплывает такое
же расстояние, как за 3 часа против течения реки. Найдите
собственную скорость лодки, если скорость течения реки равна 3 км/ч.5 этап
Слайд 122(х + 3) = 3(х – 3)
2х + 6 =
3х – 9
9 + 6 = 3х – 2х
х =
15Скорость моторной лодки 15 км/ч.
Ответ
х + 3 км/ч
х - 3 км/ч
V = 3 км/ч.
Теги
