Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мультимедийный проект "Запросы для поисковых систем. Решение задач с помощью кругов Эйлера"
Содержание
- 1. Мультимедийный проект "Запросы для поисковых систем. Решение задач с помощью кругов Эйлера"
- 2. Смысл логических связок становится более понятным, если
- 3. На рисунке представлено множество – все возможные
- 4. Задача 1."Обитаемый остров" и "Стиляги"Некоторые ребята из
- 5. Решение:Чертим два множества таким образом: 6«Стиляги»«Обитаемый остров»6 человек,
- 6. Задача 2. «Гарри Поттер, Рон и Г
- 7. Учитывая условия задачи, чертеж будет таков: Решение:427ГермионаРонГарри ПоттерТак
- 8. Задача 3.«Экстрим»Из 100 ребят, отправляющихся в детский
- 9. Решение:РоликиСкейтборд3013207325Аналогично получаем, что только на скейтборде и
- 10. Задача 4.В таблице приведены запросы и количество
- 11. Решение:При помощи кругов Эйлера изобразим условия задачи.
- 12. Решите самостоятельно:1). В таблице приведены запросы и
- 13. Решите самостоятельно:2). В таблице приведены запросы и
- 14. 3). В таблице приведены запросы и количество
- 15. 4). В таблице приведены запросы и количество
- 16. 5). В таблице приведены запросы и количество
- 17. ИБПО12348567910111213Подсказка задачи 5.
- 18. Если вы не можете определиться, какую профессию
- 19. Источники информации:http://f1.mylove.ru/0AkEJdLeQl.jpg http://logika.vobrazovanie.ru/index.php?link=kr_e.htmlhttp://inf.reshuege.ru/test?theme=256
- 20. Скачать презентанцию
Слайды и текст этой презентации
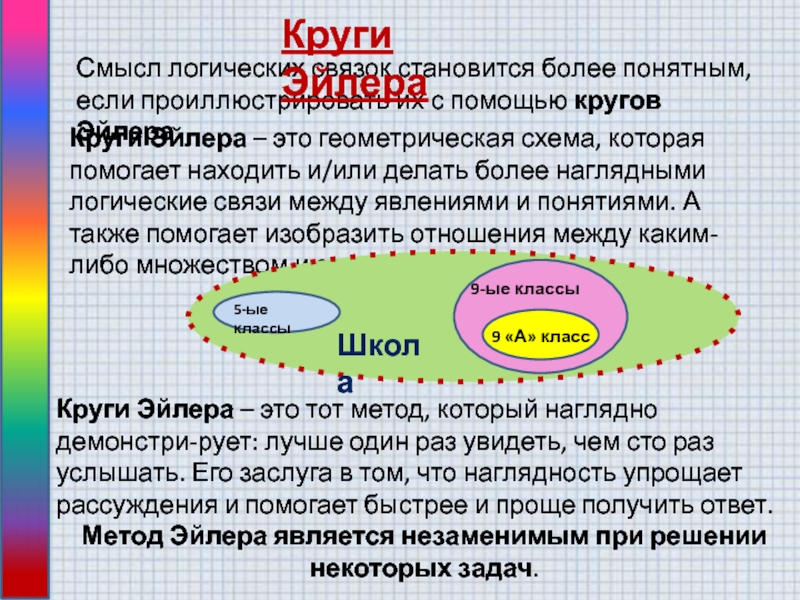
Слайд 2Смысл логических связок становится более понятным, если проиллюстрировать их с
помощью кругов Эйлера
Круги Эйлера
Круги Эйлера – это геометрическая схема, которая
помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью. Круги Эйлера – это тот метод, который наглядно демонстри-рует: лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ.
Метод Эйлера является незаменимым при решении некоторых задач.
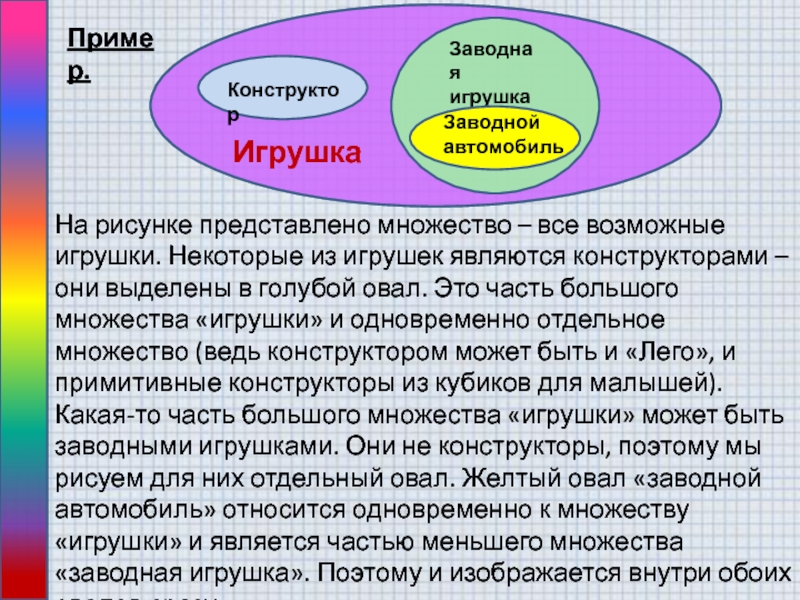
Слайд 3На рисунке представлено множество – все возможные игрушки. Некоторые из
игрушек являются конструкторами – они выделены в голубой овал. Это
часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.Пример.
Слайд 4Задача 1.
"Обитаемый остров" и "Стиляги"
Некоторые ребята из нашего класса любят
ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый
остров»11 человек смотрели фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги».
Решение:
Сколько человек смотрели
только фильм «Стиляги»?
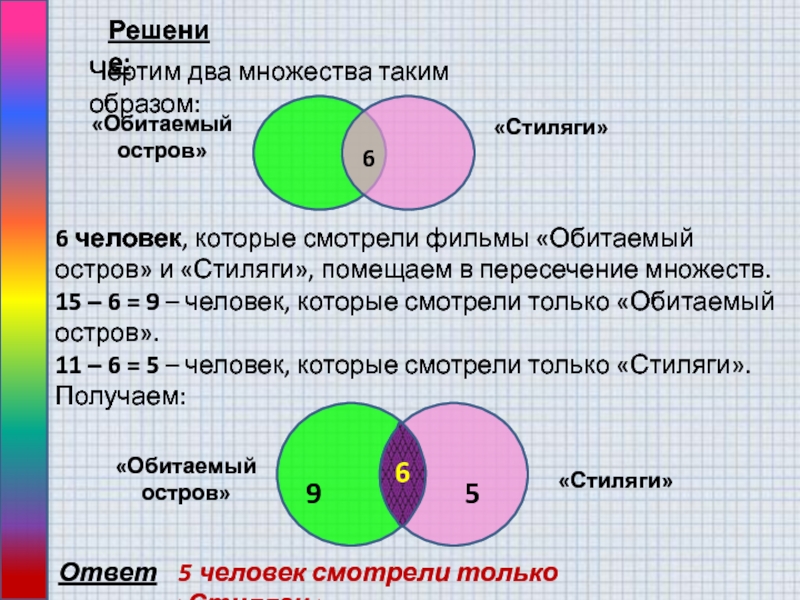
Слайд 5Решение:
Чертим два множества таким образом:
6
«Стиляги»
«Обитаемый остров»
6 человек, которые смотрели фильмы
«Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6
= 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем:«Стиляги»
«Обитаемый остров»
6
Ответ:
5 человек смотрели только «Стиляги».
Слайд 6Задача 2.
«Гарри Поттер, Рон и Г ермиона»
На полке стояло
26 волшебных книг по заклинаниям, все они были прочитаны.
Из
них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер.
Всего Гарри Поттер прочитал 11 книг.
Сколько книг прочитал только Рон?
Решение:
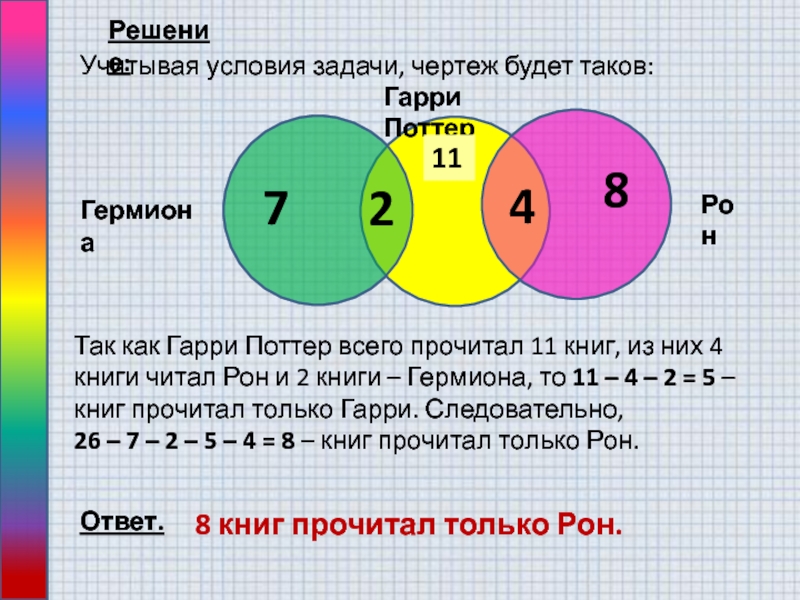
Слайд 7Учитывая условия задачи, чертеж будет таков:
Решение:
4
2
7
Гермиона
Рон
Гарри Поттер
Так как Гарри Поттер
всего прочитал 11 книг, из них 4 книги читал Рон
и 2 книги – Гермиона, то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон.Ответ.
8 книг прочитал только Рон.
11
8
Слайд 8Задача 3.
«Экстрим»
Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься
на сноуборде умеют 30 ребят, на скейтборде – 28, на
роликах – 42.На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3.
Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение:
Слайд 9Решение:
Ролики
Скейтборд
30
13
20
7
3
2
5
Аналогично получаем, что только на скейтборде и на сноуборде умеют
кататься 8-3=5 ребят, а только на сноуборде и
на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят.
Сноуборд
Ответ.
20 человек не умеют кататься ни на одном спортивном снаряде.
Слайд 10Задача 4.
В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети интернет.
Какое количество страниц (в тысячах) будет
найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одно-временно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение:
Слайд 11Решение:
При помощи кругов Эйлера изобразим условия задачи. При этом цифры
1, 2 и 3 используем, чтобы обозначить получен-ные в итоге
области.крейсер
линкор
1
2
3
Опираясь на условия задачи, составим уравнения:
Крейсер | Линкор: 1 + 2 + 3 = 7000
Крейсер: 1 + 2 = 4800
Линкор: 2 + 3 = 4500
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:
4800 + 3 = 7000, откуда получаем 3 = 2200.
Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:
2 + 2200 = 4500, откуда 2 = 2300.
Ответ:
2300 - количество страниц, найденных по запросу Крейсер & Линкор
Слайд 12Решите самостоятельно:
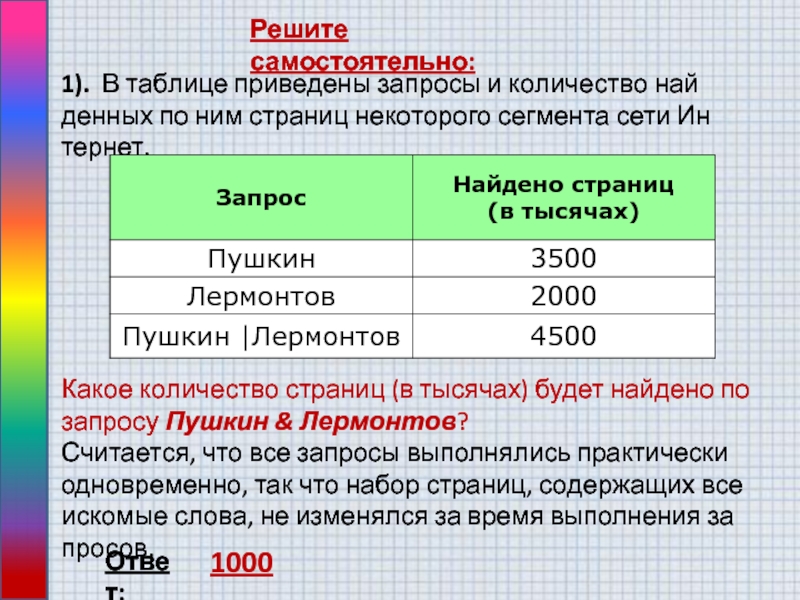
1). В таблице приведены запросы и количество найденных по
ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах)
будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ:
1000
Слайд 13Решите самостоятельно:
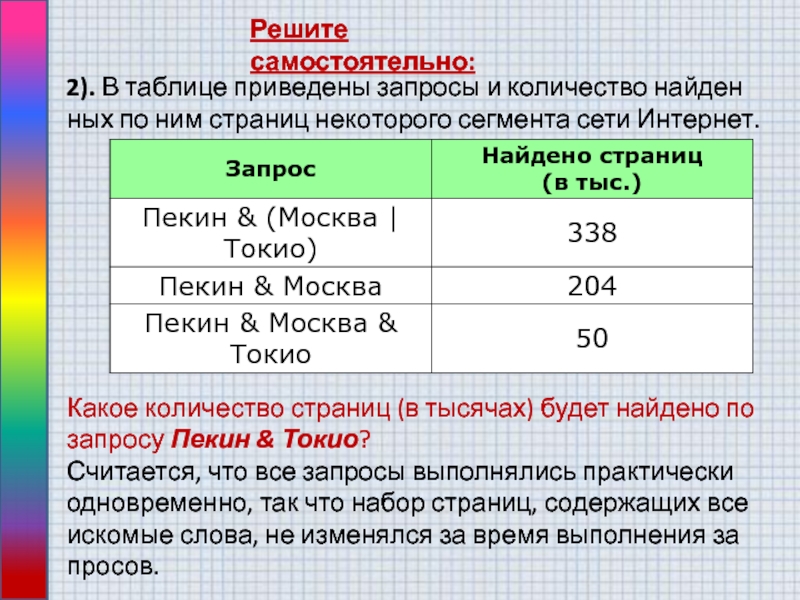
2). В таблице приведены запросы и количество найденных по
ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах)
будет найдено по запросу Пекин & Токио?Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Слайд 143). В таблице приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте Интернета:
Решите самостоятельно:
Сколько
страниц (в тысячах) будет найдено по запросувыпечка.
Ответ:
9600
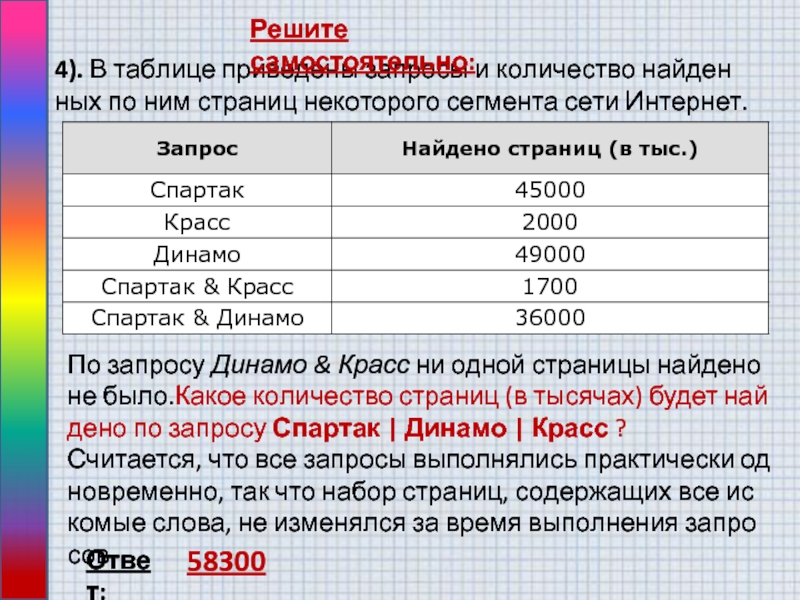
Слайд 154). В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет.
Решите самостоятельно:
По запросу Динамо & Красс ни одной
страницы найдено не было.Какое количество страниц (в тысячах) будет найдено по запросу Спартак | Динамо | Красс ?Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ:
58300
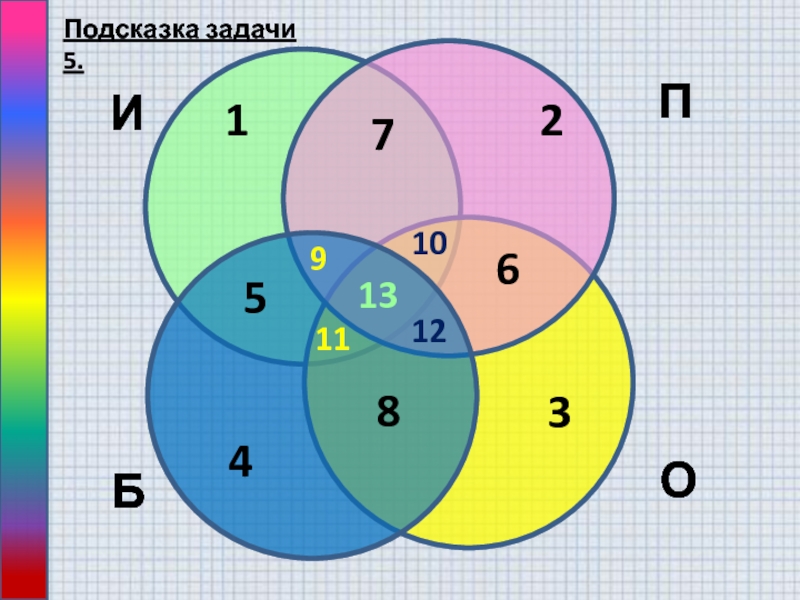
Слайд 165). В таблице приведены запросы и количество найденных по ним
страниц некоторого сегмента сети Интернет:
Решите самостоятельно:
Какое количество страниц (в тыс.)
будет найдено по запросу(Ильф & Петров & Остап)|(Ильф & Петров & Бендер)?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Ответ:
960
Подсказка
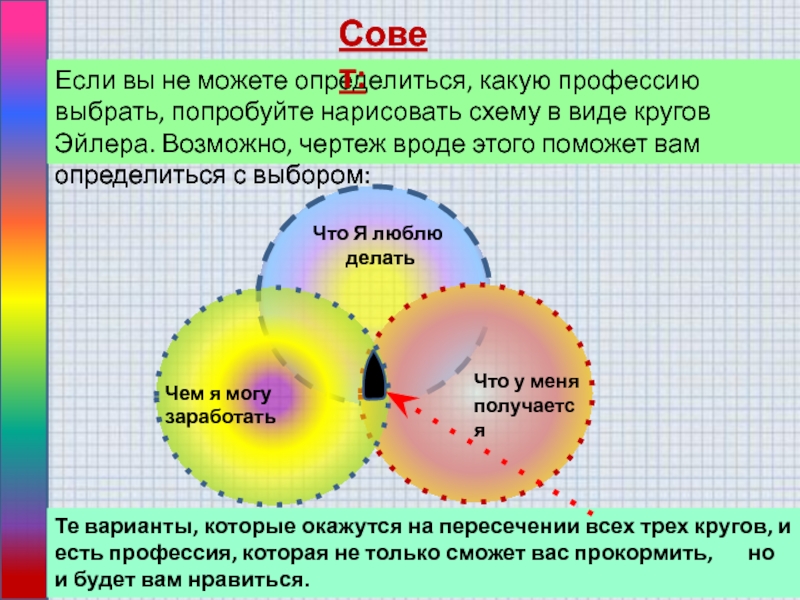
Слайд 18Если вы не можете определиться, какую профессию выбрать, попробуйте нарисовать
схему в виде кругов Эйлера. Возможно, чертеж вроде этого поможет
вам определиться с выбором:Совет:
Что Я люблю
делать
Что у меня
получается
Чем я могу
заработать
Те варианты, которые окажутся на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и будет вам нравиться.