Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация 10 класс Логика
Содержание
- 1. Презентация 10 класс Логика
- 2. ЛогикаЛогика (др.-греч. λογική — «наука о правильном
- 3. Задача логикиОдна из главных задач логики —
- 4. Современная логикаВ конце XIX — начале XX
- 5. Алгебра логики Раздел математической логики, в котором
- 6. Операции¬ - отрицание (унарная операция), /\ - конъюнкция (бинарная), V -
- 7. Операции отрицания (НЕ), конъюнкции (И) и дизъюнкции
- 8. Логические высказыванияЛогическое высказывание — это любое повествовательное
- 9. Употребляемые в обычной речи слова и словосочетания
- 10. Таблица истинности Это
- 11. Логическое «отрицание» Инверсия или НЕ. Обозначается
- 12. Попробуйте сами составит таблицу истинности: Высказывание А
- 13. Логическое умножение «И», конъюнкция (лат. conjunctio —
- 14. Таблица иcтинностиВысказывание А * В истинно тогда
- 15. Логическое сложение «Или», дизъюнкция (лат. disjunctio —
- 16. Таблица истинностиСтроим самостоятельно:Высказывание А v В ложно
- 17. Импликация (Лат. implico — тесно связаны) -
- 18. Таблица истинностиСтроим самостоятельно:Высказывание А
- 19. Эквиваленция (двойная импликация)- операция, выражаемая связками «тогда
- 20. Таблица истинностиСтроим самостоятельно:Высказывание А В
- 21. Порядок выполнения логических операций Сначала выполняется
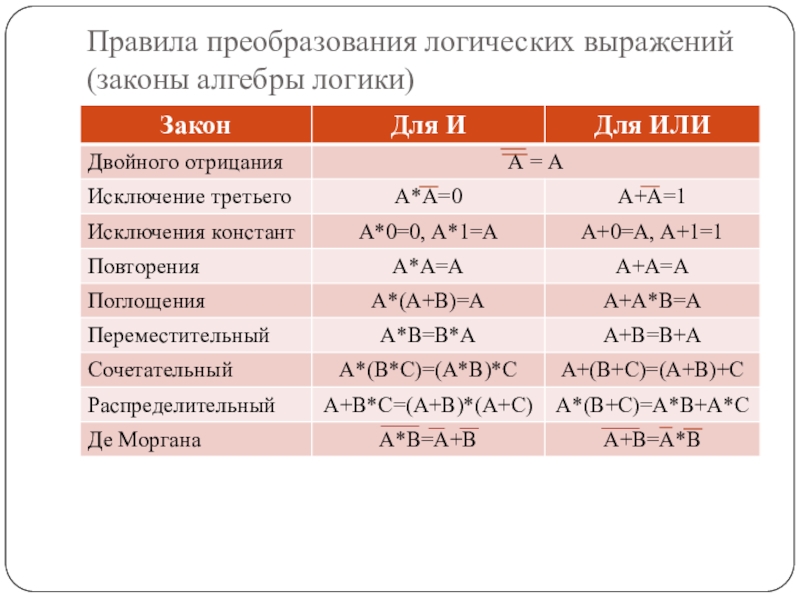
- 22. Правила преобразования логических выражений (законы алгебры логики)
- 23. Слайд 23
- 24. Слайд 24
- 25. Список использованных литературы и интернет ресурсов:В.Ю. Лыскова,
- 26. Скачать презентанцию
ЛогикаЛогика (др.-греч. λογική — «наука о правильном мышлении», «искусство рассуждения» от λόγος — «речь», «рассуждение», «мысль») — раздел философии, нормативная наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с
Слайды и текст этой презентации
Слайд 3Задача логики
Одна из главных задач логики — определить, как прийти
к выводу из предпосылок (правильное рассуждение) и получить истинное знание
о предмете размышления, чтобы глубже разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.Слайд 4Современная логика
В конце XIX — начале XX веков были заложены
основы т. н. математической, или символической, логики. Её суть заключается
в том, что для обнаружения истинностного значения выражений естественного языка можно применять математические методы. Именно использование символической логики отличает современную логическую науку от традиционной.Огромный вклад в развитие символической логики внесли такие учёные, как Дж. Буль, О. де Морган, Г. Фреге, Ч. Пирс и др.
Слайд 5Алгебра логики
Раздел математической логики, в котором изучаются логические операции
над высказываниями. Чаще всего предполагается, что высказывания могут быть только
истинными или ложными, то есть используется так называемая бинарная или двоичная логика.Высказывания строятся над множеством
{B, ¬,/\ ,V , 0, 1},
где B — непустое множество, над элементами которого определены три операции:
Слайд 6Операции
¬ - отрицание (унарная операция),
/\ - конъюнкция (бинарная),
V - дизъюнкция (бинарная),
логический ноль 0 и логическая
единица 1 — константы.
Простейший и наиболее широко применяемый пример такой алгебраической системы строится
с пользованием множества B, состоящего всего из двух элементов:B = { Ложь, Истина }
Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей.
Слайд 7Операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в
привычном нам понимании.
- эквавалетность («тогда и только тогда,
когда»),- импликация («следовательно»),
 - сложение по модулю два («исключающее или»),
- штрих Шеффера,
- стрелка Пирса и другие.
Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА).
Операции
Слайд 8Логические высказывания
Логическое высказывание — это любое повествовательное предложение, в отношении
которого можно однозначно сказать, истинно оно или ложно.
Например:
«Трава зеленая»
-истинное высказывание. «Самолет – птица» - ложное высказывание.
Всякое ли предложение является логическим высказыванием ???
Конечно нет.
Слайд 9Употребляемые в обычной речи слова и словосочетания "не", "и", "или",
"если... , то", "тогда и только тогда" и другие позволяют
из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.Высказывания, образованные из других высказываний с помощью логических связок, называются составными.
Высказывания, не являющиеся составными, называются элементарными.
Логические высказывания
Слайд 10
Таблица истинности
Это табличное представление логической схемы (операции),
в котором перечислены все возможные сочетания значений истинности входных сигналов
(операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний.Слайд 11
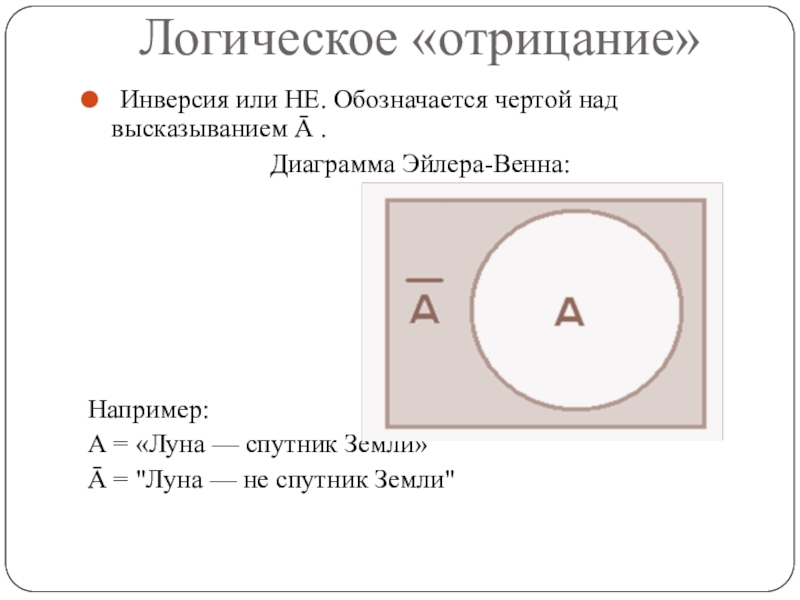
Логическое «отрицание»
Инверсия или НЕ. Обозначается чертой над высказыванием Ā .
Диаграмма
Эйлера-Венна:
Например:
А = «Луна — спутник Земли»
Ā = "Луна — не
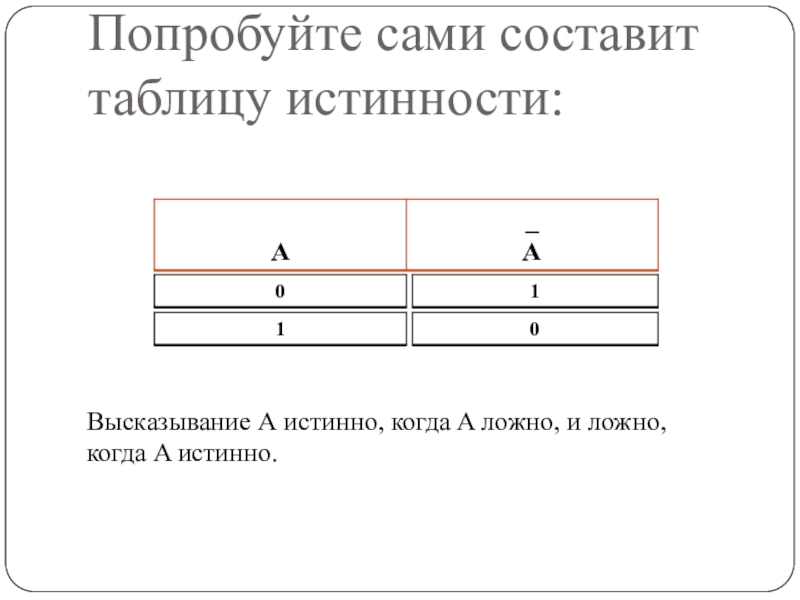
спутник Земли"Слайд 12Попробуйте сами составит таблицу истинности:
Высказывание А истинно, когда A ложно,
и ложно, когда A истинно.
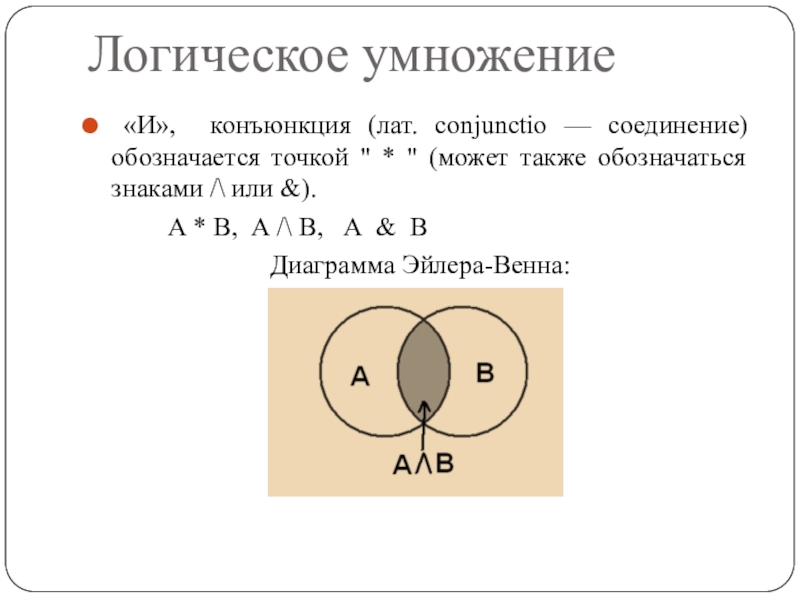
Слайд 13Логическое умножение
«И», конъюнкция (лат. conjunctio — соединение) обозначается
точкой " * " (может также обозначаться знаками /\ или
&).А * В, А /\ В, А & В
Диаграмма Эйлера-Венна:
Слайд 14Таблица иcтинности
Высказывание А * В истинно тогда и только тогда,
когда оба высказывания А и В истинны
Строим самостоятельно:
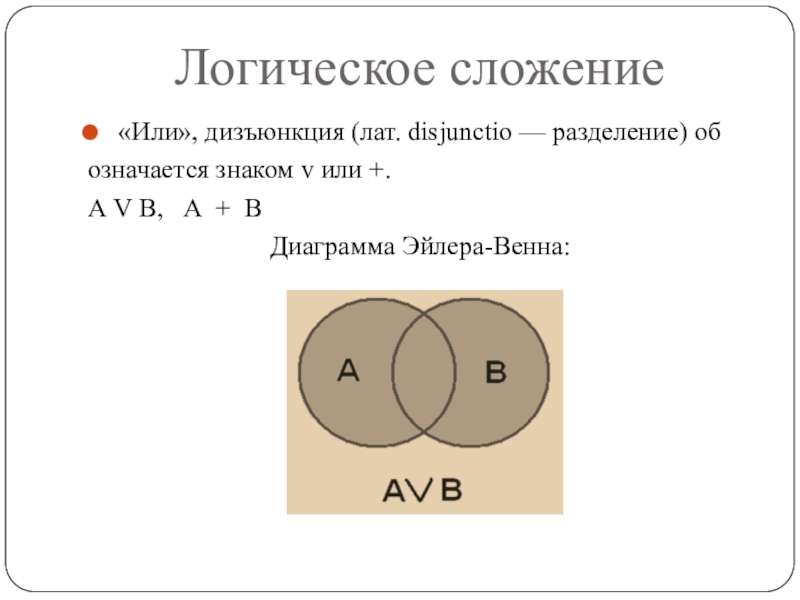
Слайд 15Логическое сложение
«Или», дизъюнкция (лат. disjunctio — разделение) об
означается знаком
v или +.
А V В, А + В
Диаграмма
Эйлера-Венна:Слайд 16Таблица истинности
Строим самостоятельно:
Высказывание А v В ложно тогда и только
тогда, когда оба высказывания А и В ложны.
Слайд 17Импликация
(Лат. implico — тесно связаны)
- операция, выражаемая связками
«если ..., то…», «из ... следует…», «... влечет ...».
Обозначается
знаком . А В
Слайд 18Таблица истинности
Строим самостоятельно:
Высказывание А В ложно
тогда и только тогда, когда А истинно, а В –
ложноСлайд 19Эквиваленция (двойная импликация)
- операция, выражаемая связками «тогда и только тогда»,
«необходимо и достаточно», «... равносильно ...» Обозначается знаком
или ~.А В, А ~ В.
Слайд 20Таблица истинности
Строим самостоятельно:
Высказывание А В истинно тогда
и только тогда, когда значения А и В совпадают
Слайд 21Порядок выполнения логических операций
Сначала выполняется операция отрицания (“не”),
Затем
конъюнкция (“и”),
После конъюнкции — дизъюнкция (“или”),
В последнюю очередь —
импликация и эквиваленция.Слайд 25Список использованных литературы и интернет ресурсов:
В.Ю. Лыскова, Е.А. Ракитина Логика
в информатике. — М. “Информатика и образование”. 1999 г.
С.С.
Коробков Элементы математической логики и теории вероятности. — Екатеринбург, 1999 М.И. Башмаков Уроки математики. Выпуск 4. Учимся логике. — Санкт-Петербург “Информатизация образования”, 2000 г.
А.П. Бойко Практикум по логике. — М. “Издательский центр АЗ”, 1997
гhttp://electrik.info/main/fakty/229-buleva-algebra-chast-1-nemnogo-istorii.html
http://www.mirea.ac.ru/d1/metodika/Indexmet.htm
http://alglib.sources.ru/articles/logic.php
http://ru.wikipedia.org/%D0%9B%D0%BE%D0%B3%D0%B8%D0%BA%D00
http://www.sch861.ru/2-school/3-11-ikt/ikt/urok/logica/2.html·
http://kpolyakov.spb.ru/school/ege.htm