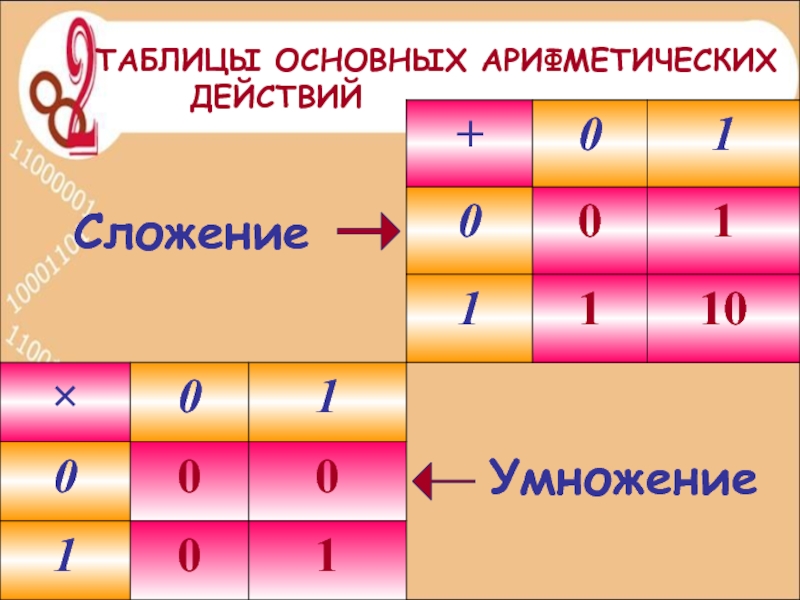
- десятичная (сложилась в Индии);
- двенадцатеричная (возникла в
Англии); 1 фут = 12 дюймов
- пятеричная (в Африке);
- двадцатеричная (сложилась у ацтеков и народов майя).
2. Шестидесятеричная (вавилонская).
1 ч = 60 мин , 1 мин = 60 сек