Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР НА ПЛОСКОСТИ
Содержание
- 1. ИЗОБРАЖЕНИЕ ПРОСТРАНСТВЕННЫХ ФИГУР НА ПЛОСКОСТИ
- 2. ВЕРНО - НЕВЕРНО ? 1. Верно ли, что
- 3. ОТВЕТЫ И ПОДСКАЗКИ Ответ: Неверно. По теореме
- 4. ВЕРНО - НЕВЕРНО ? 2. Верно ли, что
- 5. ОТВЕТЫ И ПОДСКАЗКИ Ответ: Верно. По лемме о пересечении
- 6. ВЕРНО - НЕВЕРНО ? 3. Верно ли, что две непересекающиеся прямые в пространстве параллельны?
- 7. ОТВЕТЫ И ПОДСКАЗКИсdc и d - скрещиваются3.
- 8. ВЕРНО – НЕВЕРНО? 4. Верно ли, что если
- 9. ОТВЕТЫ И ПОДСКАЗКИ 4. Ответ: неверно.Эти прямые могут
- 10. ВЕРНО – НЕВЕРНО? 5. Верно ли, что если
- 11. ОТВЕТЫ И ПОДСКАЗКИ 5. Ответ: Неверно. Это утверждение неверно
- 12. МЕТОД ПРОЕЦИРОВАНИЯ
- 13. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ
- 14. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕПроекция (от лат. projectio – бросание
- 15. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ Параллельную проекцию реальной фигуры
- 16. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
- 17. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ1. Проекция точки есть точка.2. Проекция прямой есть прямая.A0Aann0a
- 18. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ3. Проекция отрезка есть отрезок.4.
- 19. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ5. Проекции параллельных отрезков, а
- 20. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯПри параллельном проецировании сохраняются следующие
- 21. СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯПри параллельном проецировании не сохраняются
- 22. Параллельное проектирование для объемных фигур.Если рассматривать любую
- 23. Изображение плоских фигур.Фигура в пространствеЕё изображение на плоскостиПроизвольный треугольникПроизвольный треугольникРавносторонний треугольникПроизвольный треугольник
- 24. Фигура в пространствеЕё изображение на плоскостиПрямоугольный треугольникРавнобедренный треугольникПроизвольный треугольникПроизвольный треугольник
- 25. Фигура в пространствеЕё изображение на плоскостиПараллелограммПрямоугольникПроизвольный параллелограммПроизвольный параллелограммКругОвал (эллипс)
- 26. Фигура в пространствеЕё изображение на плоскостиКвадратРомбПроизвольный параллелограммПроизвольный параллелограмм
- 27. Фигура в пространствеЕё изображение на плоскостиПроизвольная трапецияПроизвольная трапецияРавнобокая трапецияПрямоугольная трапецияПроизвольная трапецияПроизвольная трапеция
- 28. Алгоритм построения изображения пирамиды.1. Изображение пирамиды начинают
- 29. Построить изображение пирамиды в основании которой лежит
- 30. Задача №2Построить изображение пирамиды в основании которой
- 31. Задача №3Построить изображение пирамиды в основании которой
- 32. Задача №4Построить изображение пирамиды в основании которой
- 33. Задача №5Построить изображение пирамиды в основании которой
- 34. 3. Строим боковые ребра, обозначаем невидимые линии,
- 35. 3. Построение боковых ребер:Вершины верхней грани призмы
- 36. Построить изображение призмы в основании которой лежит
- 37. 3. Строим боковые ребра, обозначаем невидимые линии,
- 38. Задача №3Построить изображение правильной треугольной призмы.Строим основание
- 39. Задача №4Построить изображение призмы в основании которой
- 40. Задача №5Построить изображение правильной четырехугольной призмы.Строим основание
- 41. Задача №6Построить изображение призмы в основании которой
- 42. КОНТРОЛЬНЫЕ ВОПРОСЫ1. Что является параллельной проекцией отрезка,
- 43. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2ВЕРНО - НЕВЕРНО ?
1. Верно ли, что через любую точку
пространства можно провести множество прямых параллельных данной прямой?
Слайд 3ОТВЕТЫ И ПОДСКАЗКИ
Ответ: Неверно.
По теореме о существовании прямой,
параллельной данной прямой, через точку пространства можно провести единственную прямую.
Слайд 4ВЕРНО - НЕВЕРНО ?
2. Верно ли, что если одна из
двух параллельных прямых пересекает плоскость, то и другая тоже пересекает
эту плоскость?Слайд 5ОТВЕТЫ И ПОДСКАЗКИ
Ответ: Верно.
По лемме о пересечении плоскости двумя параллельными
прямыми, если одна из параллельных прямых пересекает данную плоскость, то
и другая прямая пересекает эту плоскость.b
a
M
Слайд 7ОТВЕТЫ И ПОДСКАЗКИ
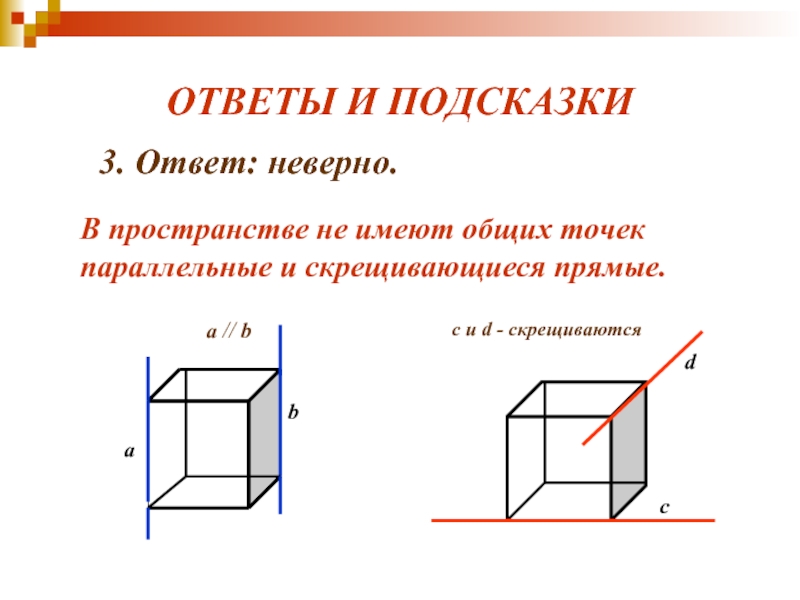
с
d
c и d - скрещиваются
3. Ответ: неверно.
В пространстве
не имеют общих точек
параллельные и скрещивающиеся прямые.
Слайд 8ВЕРНО – НЕВЕРНО?
4. Верно ли, что если две прямые параллельны
некоторой плоскости, то они параллельны друг другу?
Слайд 9ОТВЕТЫ И ПОДСКАЗКИ
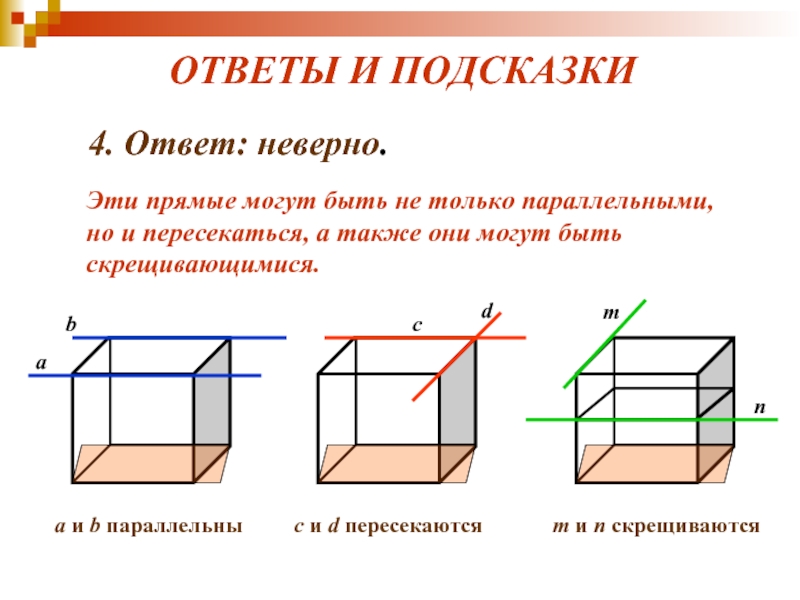
4. Ответ: неверно.
Эти прямые могут быть не только
параллельными,
но и пересекаться, а также они могут быть скрещивающимися.
a
b
c
d
m
n
a
и b параллельныс и d пересекаются
m и n скрещиваются
Слайд 10ВЕРНО – НЕВЕРНО?
5. Верно ли, что если две плоскости пересечены
двумя параллельными прямыми и отрезки данных прямых, заключённых между ними
равны, то плоскости параллельны?Слайд 11ОТВЕТЫ И ПОДСКАЗКИ
5. Ответ: Неверно.
Это утверждение неверно , так как
нет условий для выполнения признака параллельности плоскостей.
а
b
А
В
А1
В1
Если a // b
и АА1=BВ1,то плоскости могут
быть параллельны, а
могут пересекаться
А
B
C1
А1
B1
C
D1
Слайд 14ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Проекция (от лат. projectio – бросание вперёд, выбрасывание).
а
A
B
C
A1
B1
C1
N
N1
N1 – параллельная проекция точки N
Треугольник A1B1C1 – параллельная
проекция треугольника ABC
Слайд 15ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ
Параллельную проекцию реальной фигуры представляет, например, её
тень, падающая на плоскую поверхность при солнечном освещении, поскольку солнечные
лучи можно считать параллельными.Слайд 17СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
1. Проекция точки есть точка.
2. Проекция прямой есть
прямая.
A0
A
a
n
n0
a
Слайд 18СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
3. Проекция отрезка есть отрезок.
4. Проекции параллельных отрезков
– параллельные отрезки или отрезки, принадлежащие одной прямой.
a
Ao
Bo
A
B
a
Ao
Bo
A
B
Co
Do
C
D
Слайд 19СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
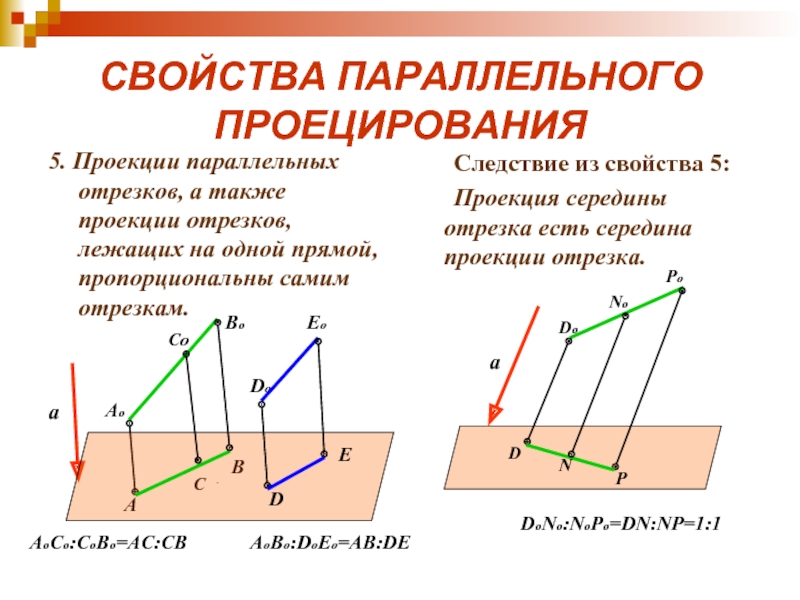
5. Проекции параллельных отрезков, а также проекции отрезков,
лежащих на одной прямой, пропорциональны самим отрезкам.
Следствие из свойства 5:
Проекция
середины отрезка есть середина проекции отрезка.a
Ao
Bo
A
B
Co
C
No
Do
Po
D
P
N
AoCo:CoBo=AC:CB
DoNo:NoPo=DN:NP=1:1
a
Do
Eo
D
E
AoBo:DoEo=AB:DE
Слайд 20СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
При параллельном проецировании сохраняются следующие свойства фигур
1.
Свойство фигуры быть точкой, прямой и
плоскостью.
2. Свойство фигур иметь
пересечение.3. Деление отрезка в данном отношении.
4. Параллельность прямых и плоскостей.
5. Свойство фигуры быть треугольником, параллелограммом, трапецией.
6. Отношение длин параллельных отрезков.
7. Отношение площадей двух фигур.
Слайд 21СВОЙСТВА ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ
При параллельном проецировании не сохраняются следующие свойства фигур:
1.
Свойство прямых и плоскостей образовывать между собой углы определенной градусной
меры (в частности быть взаимно перпендикулярными).2. Отношение длин не параллельных отрезков.
3. Отношение величин углов между прямыми
(в частности, свойство луча быть биссектрисой угла).
Слайд 22Параллельное проектирование
для объемных фигур.
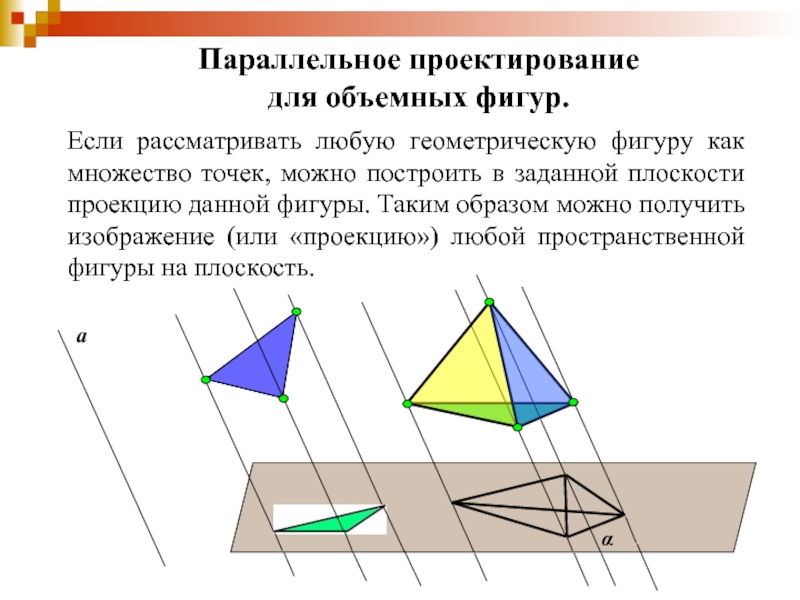
Если рассматривать любую геометрическую фигуру как
множество точек, можно построить в заданной плоскости проекцию данной фигуры.
Таким образом можно получить изображение (или «проекцию») любой пространственной фигуры на плоскость.Слайд 23Изображение плоских фигур.
Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Равносторонний
треугольник
Произвольный треугольник
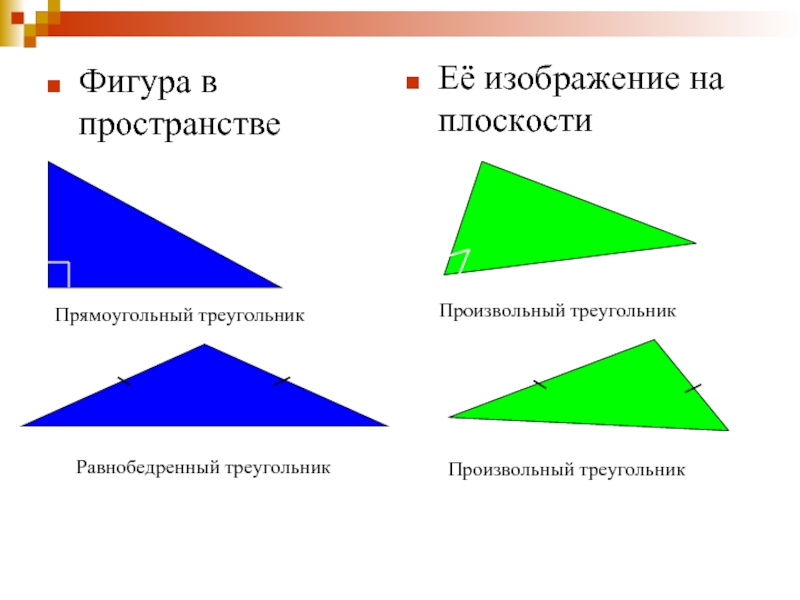
Слайд 24Фигура в пространстве
Её изображение на плоскости
Прямоугольный треугольник
Равнобедренный треугольник
Произвольный треугольник
Произвольный треугольник
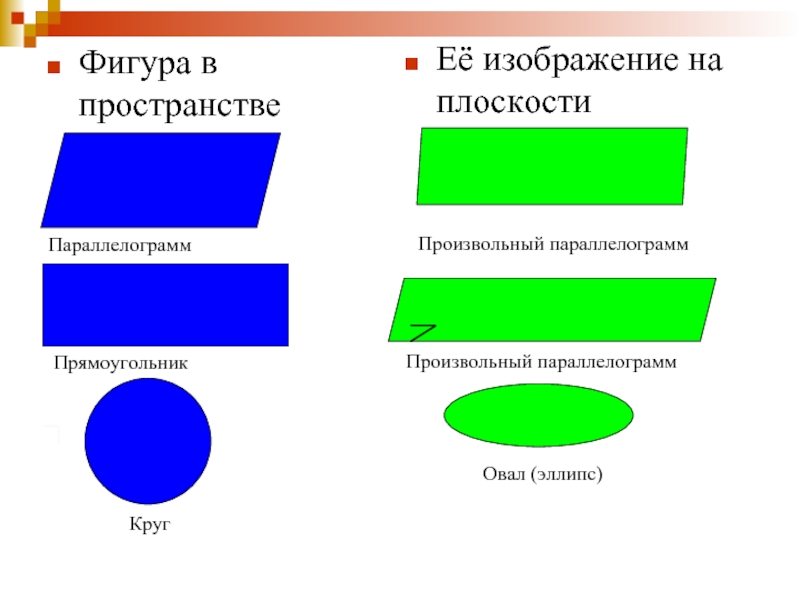
Слайд 25Фигура в пространстве
Её изображение на плоскости
Параллелограмм
Прямоугольник
Произвольный параллелограмм
Произвольный параллелограмм
Круг
Овал (эллипс)
Слайд 26Фигура в пространстве
Её изображение на плоскости
Квадрат
Ромб
Произвольный параллелограмм
Произвольный параллелограмм
Слайд 27Фигура в пространстве
Её изображение на плоскости
Произвольная трапеция
Произвольная трапеция
Равнобокая трапеция
Прямоугольная трапеция
Произвольная
трапеция
Произвольная трапеция
Слайд 28Алгоритм построения изображения пирамиды.
1. Изображение пирамиды начинают всегда с изображения
ее основания:
Вершины основания пирамиды выбираем так, чтобы получить наиболее наглядное
изображение;Далее вершины соединяются тонкой вспомогательной линией;
2. Построение высоты пирамиды:
Исходя из свойств пирамиды и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
3. Построение боковых ребер:
Вершина пирамиды соединяется отрезками с вершинами основания.
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
Слайд 29Построить изображение пирамиды в основании которой лежит равнобедренный треугольник.
Задача №1
Здесь
и в дальнейшем строить изображение пирамиды будем согласно приведенному алгоритму.Строим основание пирамиды.
Равнобедренный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
Одним из таких перпендикуляров будет медиана, проведенная к основанию треугольника.
На проекционном чертеже основание высоты занимает произвольное местоположение на проведенной медиане.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 30Задача №2
Построить изображение пирамиды в основании которой лежит прямоугольный треугольник.
Строим
основание пирамиды.Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 31Задача №3
Построить изображение пирамиды в основании которой лежит правильный треугольник.
Строим
основание пирамиды.Правильный треугольник изображается произвольным треугольником.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании правильный треугольник, поэтому основание высоты – точка пересечения его медиан.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
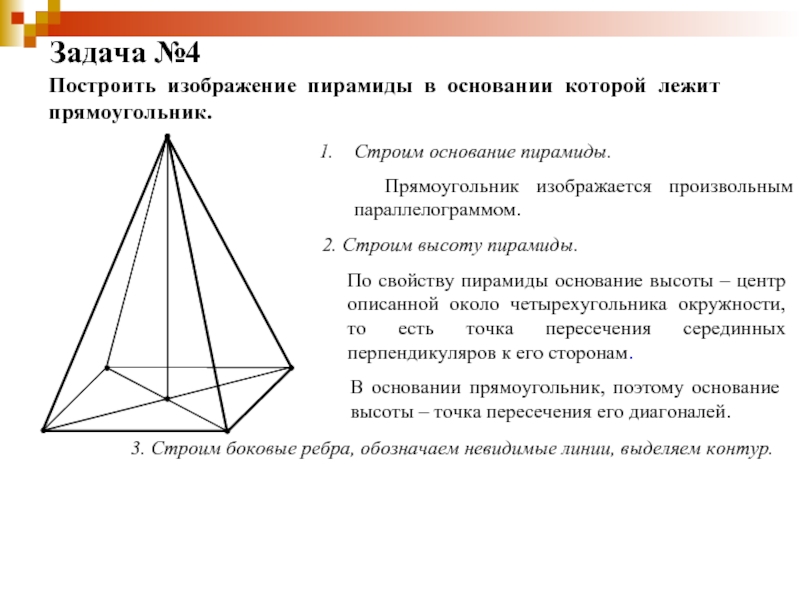
Слайд 32Задача №4
Построить изображение пирамиды в основании которой лежит прямоугольник.
Строим основание
пирамиды.Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
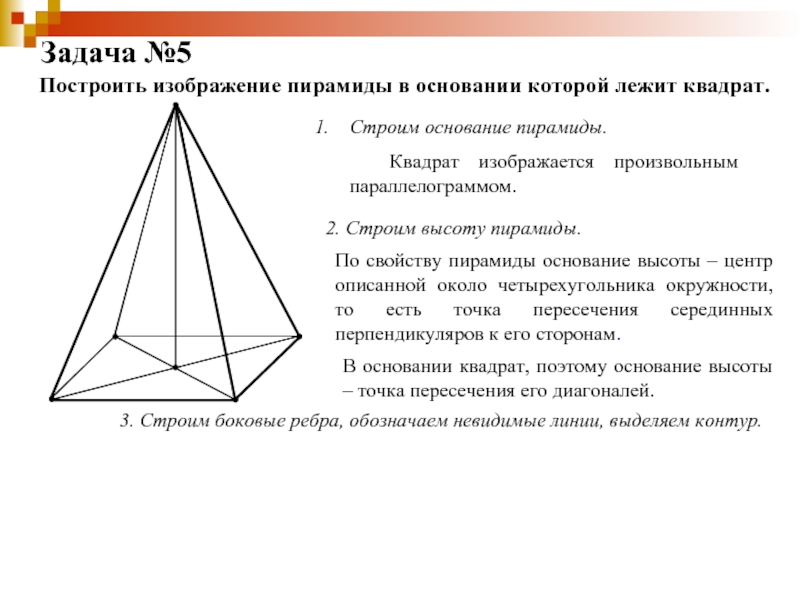
Слайд 33Задача №5
Построить изображение пирамиды в основании которой лежит квадрат.
Строим основание
пирамиды.Квадрат изображается произвольным параллелограммом.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании квадрат, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 343. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
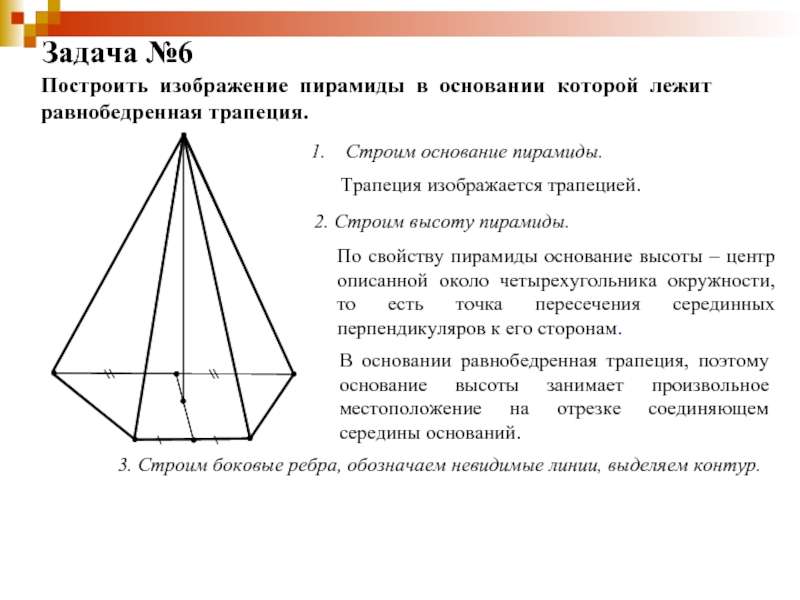
Задача №6
Построить
изображение пирамиды в основании которой лежит равнобедренная трапеция.
Строим основание пирамиды.
Трапеция изображается трапецией.
2. Строим высоту пирамиды.
По свойству пирамиды основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании равнобедренная трапеция, поэтому основание высоты занимает произвольное местоположение на отрезке соединяющем середины оснований.
Слайд 353. Построение боковых ребер:
Вершины верхней грани призмы соединяются отрезками с
вершинами основания.
4. Невидимые отрезки отмечаем штриховой линией.
5. Выделяем контур.
Алгоритм изображения
призмы.1. Изображение призмы начинают всегда с изображения ее основания:
Вершины основания призмы выбираем так, чтобы получить наиболее наглядное изображение;
Далее вершины соединяются тонкой вспомогательной линией;
2. Построение высоты призмы:
Исходя из свойств призмы и свойств многоугольника, лежащего в основании строится основание высоты;
Высота изображается вертикальным отрезком, параллельным краю листа бумаги.
Слайд 36Построить изображение призмы в основании которой лежит равнобедренный треугольник.
Задача №1
Здесь
и в дальнейшем строить изображение призмы будем согласно приведенному алгоритму.Строим основание призмы
Равнобедренный треугольник изображается произвольным треугольником.
2. Строим высоту призмы.
По свойству призмы основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
Одним из таких перпендикуляров будет медиана, проведенная к основанию треугольника.
На проекционном чертеже основание высоты занимает произвольное местоположение на проведенной медиане.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 373. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Задача №2
Построить
изображение призмы в основании которой лежит прямоугольный треугольник.
Строим основание призмы.
Прямоугольный треугольник изображается произвольным треугольником.
2. Строим высоту призмы.
По свойству пирамиды основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольный треугольник, поэтому основание высоты – середина гипотенузы.
Слайд 38Задача №3
Построить изображение правильной треугольной призмы.
Строим основание призмы.
Правильный
треугольник изображается произвольным треугольником.
2. Строим высоту призмы.
По свойству призмы
основание высоты – центр описанной около треугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.В основании правильный треугольник, поэтому основание высоты – точка пересечения его медиан.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 39Задача №4
Построить изображение призмы в основании которой лежит прямоугольник.
Строим основание
призмы.Прямоугольник изображается произвольным параллелограммом.
2. Строим высоту призмы.
По свойству призмы основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании прямоугольник, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 40Задача №5
Построить изображение правильной четырехугольной призмы.
Строим основание призмы.
Квадрат
изображается произвольным параллелограммом.
2. Строим высоту призмы.
По свойству призмы основание
высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.В основании квадрат, поэтому основание высоты – точка пересечения его диагоналей.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
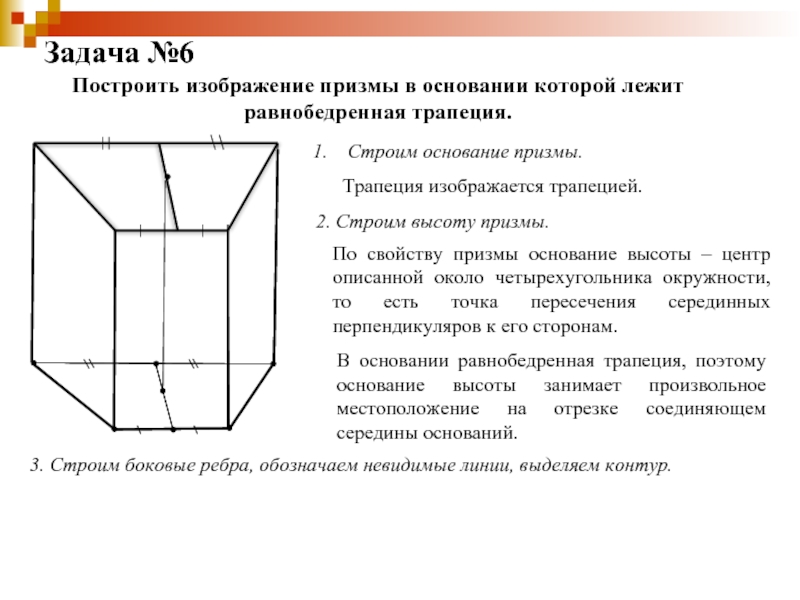
Слайд 41Задача №6
Построить изображение призмы в основании которой лежит равнобедренная трапеция.
Строим
основание призмы.Трапеция изображается трапецией.
2. Строим высоту призмы.
По свойству призмы основание высоты – центр описанной около четырехугольника окружности, то есть точка пересечения серединных перпендикуляров к его сторонам.
В основании равнобедренная трапеция, поэтому основание высоты занимает произвольное местоположение на отрезке соединяющем середины оснований.
3. Строим боковые ребра, обозначаем невидимые линии, выделяем контур.
Слайд 42КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что является параллельной проекцией отрезка, треугольника, прямоугольника, квадрата,
окружности?
2. Какие величины не изменяются при параллельном проецировании? (длина отрезка,
градусная мера углов, отношения длин отрезков, отношение площадей двух фигур)?3. Может ли при параллельном проецировании параллелограмма получиться трапеция и наоборот?