Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математика в Древнем Египте
Содержание
- 1. Математика в Древнем Египте
- 2. Древнейшие древнеегипетские математические тексты относятся к началу
- 3. ИсточникиОсновные сохранившиеся источники относятся к периоду Среднего царства,
- 4. От Нового царства до нас дошли несколько фрагментов вычислительного
- 5. Полностью отсутствуют какие бы то ни было
- 6. Нумерация (запись чисел) Древнеегипетская нумерация, то есть
- 7. Иероглифы для изображения чисел
- 8. Умножение египтяне производили с помощью сочетания удвоений и
- 9. Арифметика
- 10. Знаки сложения и вычитания.Сложение Чтобы показать знаки
- 11. Умножение Древнеегипетское умножение является последовательным методом умножения
- 12. Разложение. Уравнение Египтяне использовали систему разложения наименьшего
- 13. Геометрия В области геометрии египтяне знали точные
- 14. Египетский треугольник. Объём усечённого конуса Египетским треугольником
- 15. Скачать презентанцию
Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и
Слайды и текст этой презентации
Слайд 2Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до
н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при
строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было.Уровень древнеегипетской математики был довольно высок. Источников, по которым можно судить об уровне математических знаний древних египтян, совсем немного.
Слайд 3Источники
Основные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской
культуры:
Папирус Ахмеса или папирус Ринда — наиболее объёмный манускрипт, содержащий 84 математические
задачи. Написан около 1650 г. до н. э.Московский математический папирус (25 задач), около 1850 г. до н. э., 544 × 8 см.
Так называемый «кожаный свиток», 25 × 43 см.
Папирусы из Лахуна (Кахуна), содержащие ряд фрагментов на математические темы.
Берлинский папирус, около 1300 года до н. э.
Каирские деревянные таблички (таблички Ахмима).
Папирус Рейснера, примерно XIX век до н. э.
Слайд 4От Нового царства до нас дошли несколько фрагментов вычислительного характера.
Авторы всех этих
текстов нам неизвестны. Дошедшие до нас экземпляры — это в основном
копии, переписанные в период гиксосов. Носители научных знаний тогда именовались писцамии фактически были государственными или храмовыми чиновниками.Все задачи из папируса Ахмеса (записан ок. 1650 года до н. э.) имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным .
Слайд 5Полностью отсутствуют какие бы то ни было объяснения или доказательства.
Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления.
Такой способ
изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём индуктивных обобщений и гениальных догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или, по крайней мере, начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры: при решении уравнений специальный иероглиф «куча» обозначал неизвестное.Слайд 6Нумерация (запись чисел)
Древнеегипетская нумерация, то есть запись чисел, была похожа
на римскую: поначалу были отдельные значки для 1, 10, 100,
… 10 000 000, сочетавшиеся аддитивно (складываясь). Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. В иератическом письме уже есть отдельные обозначения для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч.Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. Например, чтобы написать число 30, можно было использовать обычные иероглифы:
или то же самое написать цифрами (три символа десятки):
Иероглифическая запись числа 35736
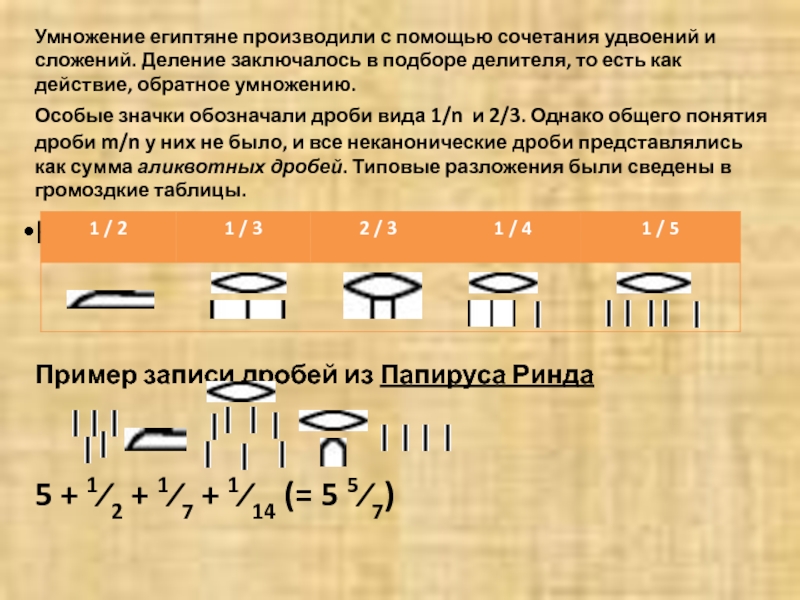
Слайд 8Умножение египтяне производили с помощью сочетания удвоений и сложений. Деление заключалось
в подборе делителя, то есть как действие, обратное умножению.
Особые значки
обозначали дроби вида 1/n и 2/3. Однако общего понятия дроби m/n у них не было, и все неканонические дроби представлялись как сумма аликвотных дробей. Типовые разложения были сведены в громоздкие таблицы.Hh
Пример записи дробей из Папируса Ринда
5 + 1⁄2 + 1⁄7 + 1⁄14 (= 5 5⁄7)
Слайд 10Знаки сложения и вычитания.Сложение
Чтобы показать знаки сложения или вычитания использовался
иероглиф: или
Если направление ног у
этого иероглифа совпадало с направлением письма, тогда он означал «сложение», в других случаях он означал «вычитание».Сложение
Если при сложении получается число большее десяти, тогда десяток записывается повышающим иероглифом.
Например: 2343 + 1671
Слайд 11Умножение
Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать
числа, им не нужно было знать таблицы умножения, а достаточно
было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать.Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное переумножение на второй множитель (см. пример).
Этот метод можно и сегодня встретить в очень отдаленных регионах.
Слайд 12Разложение. Уравнение
Египтяне использовали систему разложения наименьшего множителя на кратные числа,
сумма которых составляла бы исходное число.
Чтобы правильно подобрать кратное число,
нужно было знать следующую таблицу значений: 1 x 2 = 2 2 x 2 = 4 4 x 2 = 8 8 x 2 = 16 16 x 2 = 32Пример разложения числа 25: Кратный множитель для числа «25» — это 16. 25 — 16 = 9,
Кратный множитель для числа «9» — это 8, 9 — 8 = 1,
Кратный множитель для числа «1» — это 1, 1 — 1 = 0
Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1.
Пример: умножим «13» на «238»:
1х238=238 4х238=952 8х238=1904 13х238=3094
Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094
Уравнения
Пример задачи из папируса Ахмеса:
Найти число, если известно, что от прибавления к нему 2/3 его и вычитания из результата его трети получается 10.
х(2/3+1/2+1/7+1)=37
Слайд 13Геометрия
В области геометрии египтяне знали точные формулы для площади прямоугольника,
треугольника, трапеции и сферы, могли высчитывать объемы параллелепипеда, цилиндра и
пирамид. Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как S=(a+c)/2*(b+d)/2 эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику.Египтяне предполагали, что площадь круга S диаметром d равна площади квадрата, сторона которого составляет 8/9 диаметра: S=(d-d/9)^2=(8/9d)^2
Это правило соответствует значению П=4*(8/9)^2 (≈ 3,1605, погрешность менее 1 %)
Ещё одна ошибка содержится в Акмимском папирусе : автор считает, что если радиус круга A есть среднее арифметическое радиусов двух других кругов B и C, то и площадь круга A есть среднее арифметическое площадей кругов B и C.
Вычисление объёма усечённой пирамиды: пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле:
V=(a^2+ab+b^2)*h/3
Слайд 14Египетский треугольник.
Объём усечённого конуса
Египетским треугольником называется прямоугольный треугольник с соотношением
сторон 3:4:5.
Объём усечённого конуса
Древний свиток папируса, найденный в Оксиринхе, свидетельствует, что
египтяне могли вычислять объем усеченного конуса. Эти знания ими использовались для сооружения водяных часов. Так, например, известно, что при Аменхотепе III были построены водяные часы в Карнаке.Реконструкция водяных часов по чертежам из Оксиринха