Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение линейных неравенств
Содержание
Слайды и текст этой презентации
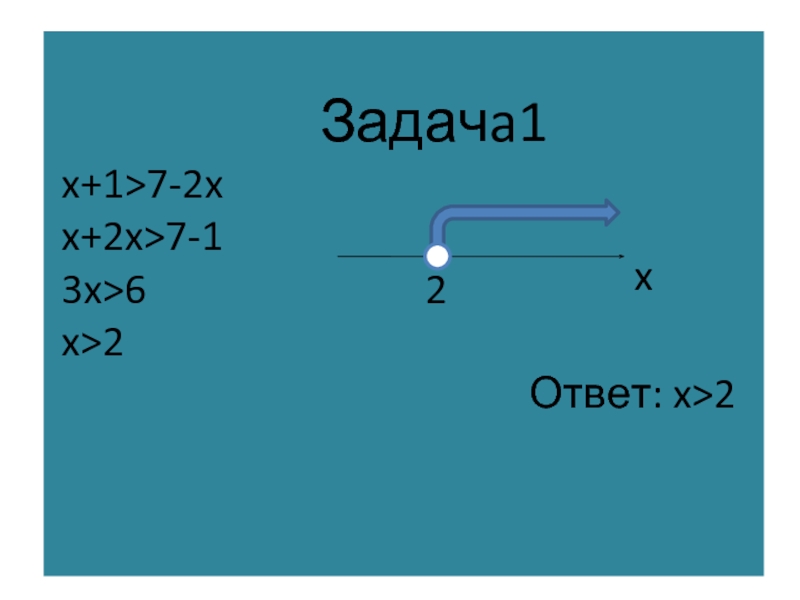
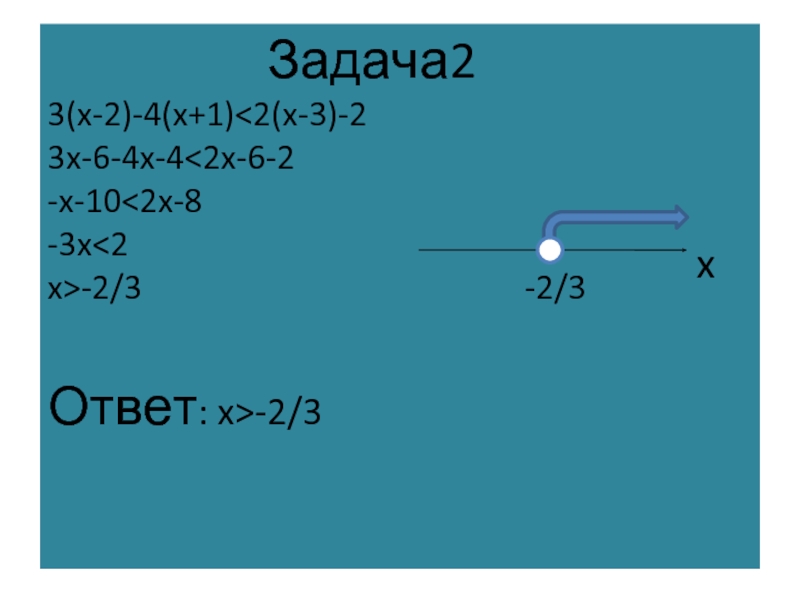
Слайд 3Для решения неравенства с одним неизвестным, которое сводится к линейному,
нужно: 1) Перенести члены содержащие неизвестное, в левую часть, а члены,
не содержащие неизвестное, в правую (свойство1) 2) Приведя подобные члены, разделить обе части неравенства на коэффициент при неизвестном, если он не равен нулю (свойство2 )Слайд 6 Выполните задания 1.(x+3)(x-2)>(x+2)(x-3) 2. (x+1)(x-4)+4>(x+2)(x-3) 3. 3(2x-1)+3(x-1)>5(x+2)+2(2x-3) 4.
5(x+2)-x>3(x-1)+x 5. 6x+5>0 6. 4(2-x)
Теги