Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Фрактальная геометрия
Содержание
- 1. Фрактальная геометрия
- 2. Что такое геометрия?раздел математики, изучающий пространственные структуры
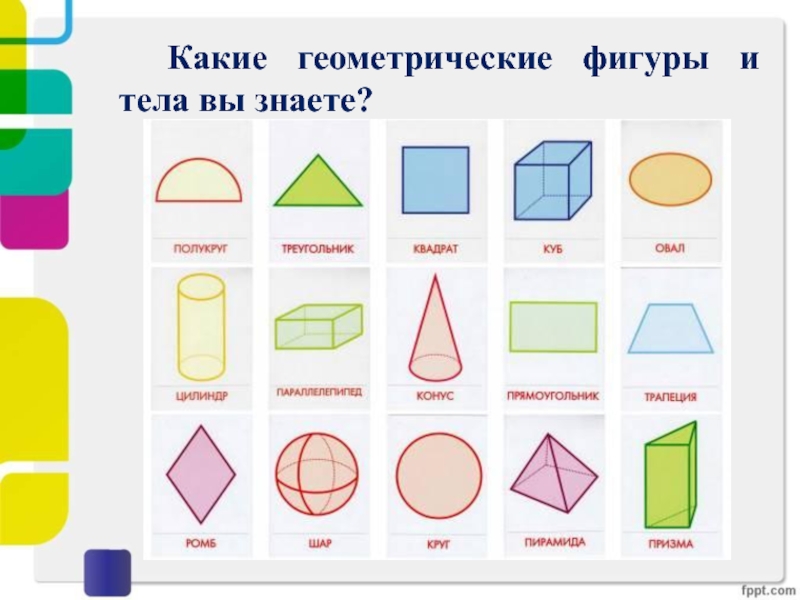
- 3. Какие геометрические фигуры и тела вы знаете?
- 4. Все ли объекты можно описать с помощью
- 5. Красота природы безгранична И сложными объектами полна
- 6. изучить теорию фракталов для развития познавательного интереса
- 7. Пыль КантораПервые идеи фрактальной геометрии возникли еще
- 8. Бенуа Мандельброт и его книга «Фрактальная геометрия природы» 1977год
- 9. Что такое фрактал? Фрактал (лат. fractus —
- 10. Свойства фракталовОбладает нетривиальной структурой на всех масштабах.
- 11. Типы фракталов
- 12. Геометрические фракталы по-другому называют классическими. Они являются
- 13. Посмотрим как получаются геометрические фракталы https://www.youtube.com/watch?v=d1eAGI5YDcY
- 14. Какие фракталы мы увидели? Снежинка КохаПолучается из
- 15. Пятиугольник Дюрера Фрактал «Пятиугольник Дюрера» был назван в
- 16. Салфетка СерпинскогоЭтот фрактал описал в 1915 году
- 17. Кривая драконаИзобретена итальянским математиком Джузеппе Пеано. Берется
- 18. Ковер Серпинского Берется квадрат, разбивается на девять
- 19. Как вы думаете почему же фрактальная геометрия
- 20. Приведите примеры фракталов, которые есть в живой природе
- 21. Применение фракталов
- 22. Пейзаж в виде формулидея использовать в качестве фона изображение гор в 1977 г. Лорена Карпентера
- 23. Организм человекаЧеловеческий организм состоит из множества фрактальных структур: кровеносная система, мышцы, бронхи и т.д.
- 24. Фракталы в медицинеОбласть активного применения фракталов –гастроэнтерология.
- 25. Фракталы в медицинеТеория фракталов применятся для анализа
- 26. Примером одного из наиболее эффективных применений
- 27. Фрактальная графикаВ играх. Создано большое количество программ
- 28. Изучение турбулентностиИзучение турбулентности в потоках очень хорошо
- 29. Практическая работаДвигаясь непрерывно по квадрату пройти по
- 30. Практическая работаРаботу выполнить на предложенном листе:
- 31. Синквейн по теме урока1 строка - тема синквейна
- 32. Я понятие
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Фрактальная геометрия
Преподаватель: Шалдина А.В.
Дисциплина: ОУД.04 «Математика» (включая алгебру и начала
математического анализа, геометрию)
Слайд 2Что такое геометрия?
раздел математики, изучающий пространственные структуры и отношения, а
также их обобщения. Геометрия как систематическая наука появилась в Древней Греции, её
аксиоматические построения описаны в «Началах» Евклида.Слайд 4Все ли объекты можно описать с помощью известных нам геометрических
фигур?
Свод правил евклидовой геометрии не способен описать форму облака, горы,
дерева или берега моря. Облака – это не сферы, горы – не конусы, берега – не окружности и кора дерева не является гладкой, и молния не движется по прямой… Слайд 5
Красота природы безгранична
И сложными объектами полна
А то, что геометрии привычно
Не
удаётся описать сполна.
Берег моря, облако иль пламя
Как их форму можно
описать?
Чтобы приоткрыть завесу тайн
Нужно мир фракталов изучать.Так что же мы будем
сегодня изучать?
Слайд 6изучить теорию фракталов для развития познавательного интереса и мотивации студентов
в процессе изучения геометрии. Показать взаимосвязь математики с другими науками
(физикой, биологией)Задачи урока:
познакомиться с историей возникновения и развития фрактальной геометрии;
изучить виды геометрических фракталов, их применение в современном мире;
закрепить полученные знания с помощью выполнения практического задания.
Цель урока:
Слайд 7Пыль Кантора
Первые идеи фрактальной геометрии возникли еще в XIX веке.
Кантор с помощью простой рекурсивной процедуры превратил линию в набор
несвязанных точек (так называемая пыль Кантора). Он брал линию и удалял центральную треть и после этого повторял то же самое с оставшимися отрезками.Слайд 9Что такое фрактал?
Фрактал (лат. fractus — дроблёный, сломанный, разбитый)
- математическое множество, обладающее свойством самоподобия (объект, в точности или
приближённо совпадающий с частью себя самого, то есть целое имеет ту же форму, что и одна или более частей)Слайд 10Свойства фракталов
Обладает нетривиальной структурой на всех масштабах. Для фрактала увеличение
масштаба не ведёт к упрощению структуры, то есть на всех
шкалах мы увидим одинаково сложную картину.Является самоподобным или приближённо самоподобным (иными словами, любая часть фрактала похожа на весь фрактал в целом; так, отдельная ветка на дереве напоминает по строению все дерево, а часть листа папоротника — весь лист).
Слайд 12Геометрические фракталы по-другому называют классическими.
Они являются самыми наглядными,
так как обладают так называемой жесткой самоподобностью, не изменяющейся при
изменении масштаба.Независимо от того, насколько вы приближаете фрактал, вы видите всё тот же узор.
Геометрические фракталы
Слайд 13Посмотрим как получаются геометрические фракталы
https://www.youtube.com/watch?v=d1eAGI5YDcY
Слайд 14Какие фракталы мы увидели?
Снежинка Коха
Получается из трех копий кривой Коха, которая
впервые появилась в статье шведского математика Хельге фон Коха в 1904 году.
Она непрерывна, но нигде не дифференцируема. Имеет бесконечную длину. Снежинка Коха ограничивает конечную площадь.Слайд 15Пятиугольник Дюрера
Фрактал «Пятиугольник Дюрера» был назван в честь немецкого живописца
и графика Альбрехта Дюрера. Именно он в 1525 изобретает правило
построения правильного пятиугольника. «Звезда Дюрера» выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей, в которых в точности равно так называемой «золотой пропорции» в качестве генератора.Слайд 16Салфетка Серпинского
Этот фрактал описал в 1915 году польский математик Вацлав
Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью,
провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага.Слайд 17Кривая дракона
Изобретена итальянским математиком Джузеппе Пеано. Берется отрезок прямой. На
каждом шаге отрезок заменяется на ломаную из двух равных отрезков,
составляющих прямой угол между собой. Направление вершины угла определяется так, чтобы никакие два соседних отрезка в образовавшейся фигуре не лежали на одной прямой.Слайд 18Ковер Серпинского
Берется квадрат, разбивается на девять равных квадратов, средний
из которых выбрасывается, а с остальными повторяется та же операция
до бесконечности.Слайд 19Как вы думаете почему же фрактальная геометрия появилась так поздно?
До
70-х годов ХХ века существовал недостаток вычислительных мощностей
Слайд 22Пейзаж в виде формул
идея использовать в качестве фона изображение гор
в 1977 г. Лорена Карпентера
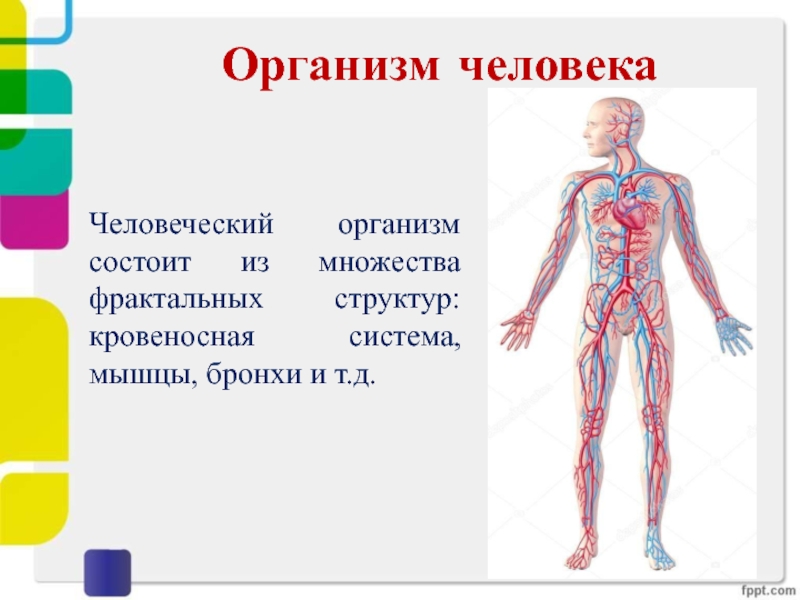
Слайд 23Организм человека
Человеческий организм состоит из множества фрактальных структур: кровеносная система,
мышцы, бронхи и т.д.
Слайд 24Фракталы в медицине
Область активного применения фракталов –гастроэнтерология.
Новый метод
исследования в медицине, электрогастроэнтерография — метод исследования, позволяющий оценить биоэлектрическую
активность желудка, двенадцатиперстной кишки и других отделов ЖКТ.Слайд 25Фракталы в медицине
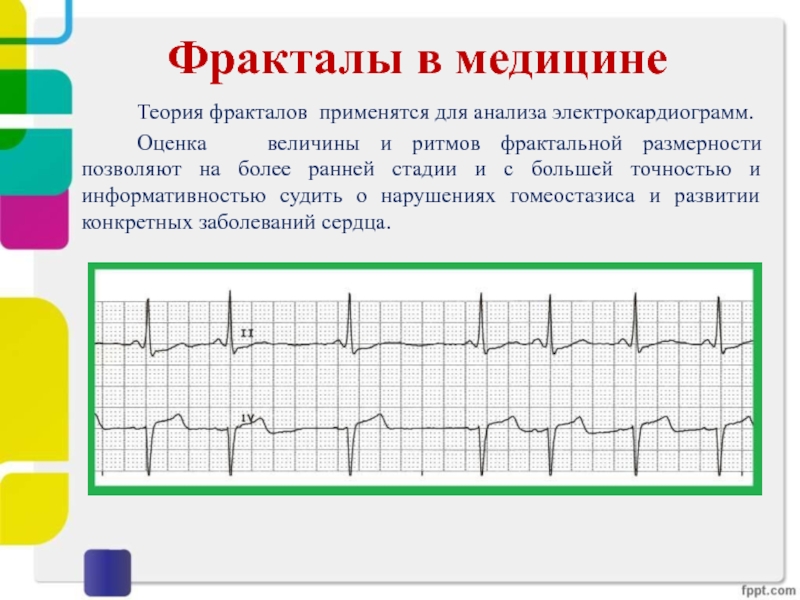
Теория фракталов применятся для анализа электрокардиограмм.
Оценка
величины и ритмов фрактальной размерности позволяют на более ранней стадии
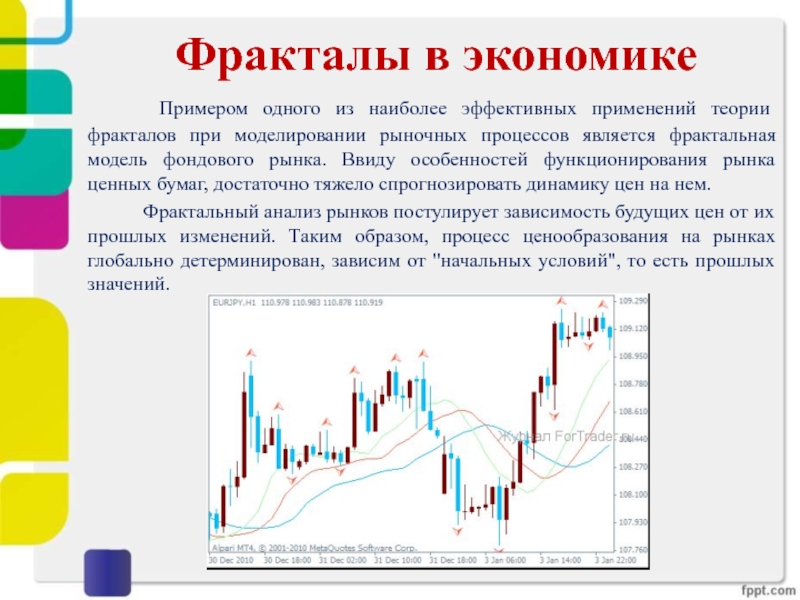
и с большей точностью и информативностью судить о нарушениях гомеостазиса и развитии конкретных заболеваний сердца.Слайд 26 Примером одного из наиболее эффективных применений теории фракталов при
моделировании рыночных процессов является фрактальная модель фондового рынка. Ввиду особенностей
функционирования рынка ценных бумаг, достаточно тяжело спрогнозировать динамику цен на нем.Фрактальный анализ рынков постулирует зависимость будущих цен от их прошлых изменений. Таким образом, процесс ценообразования на рынках глобально детерминирован, зависим от "начальных условий", то есть прошлых значений.
Фракталы в экономике
Слайд 27Фрактальная графика
В играх. Создано большое количество программ для генерации ландшафтов
и пейзажей, основанных на фрактальных алгоритмах.
в кино для создания различных
фантастических пейзажейСлайд 28Изучение турбулентности
Изучение турбулентности в потоках очень хорошо подстраивается под фракталы.
Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать.
Здесь
помогает переход к из фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных системСлайд 29Практическая работа
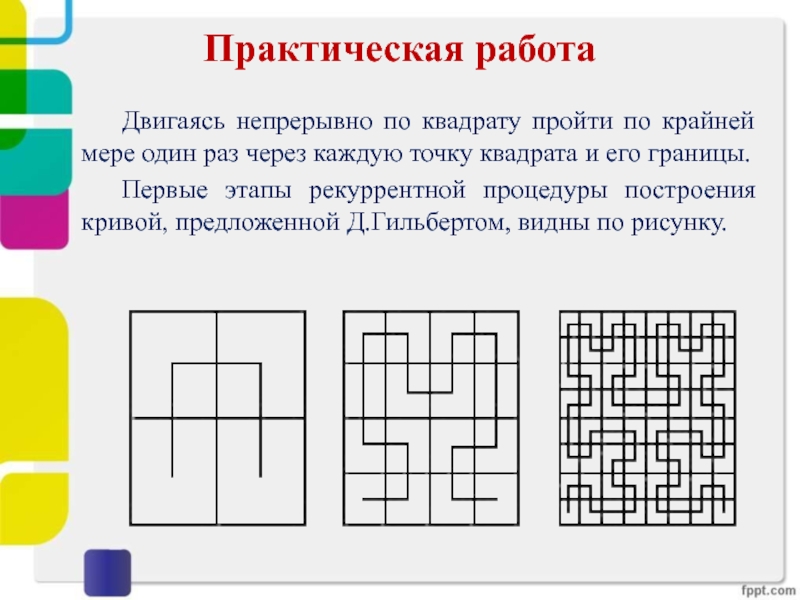
Двигаясь непрерывно по квадрату пройти по крайней мере один
раз через каждую точку квадрата и его границы.
Первые этапы
рекуррентной процедуры построения кривой, предложенной Д.Гильбертом, видны по рисунку.Слайд 31Синквейн по теме урока
1 строка - тема синквейна - одно слово (существительное
или местоимение, обозначающее объект, о котором дальше пойдет речь)
2 строка
- 2 слова (прилагательное или причастие, они описывают свойства или признаки выбранного объекта)3 строка - 3 глагола или деепричастия, которые описывают действия, характерные для объекта.
4 строка - фраза из 4 слов, в которой автор выражает свое личное отношение к объекту, о котором идёт речь.
5 строка - одно слово-резюме, дающее характеристику объекту.
Слайд 32 Я понятие фрактал – ломанный,
разбитый И красив и статен я, из частей весь свитый. Ключевое свойство
моё – самоподобие В уменьшенном масштабе – я снова своя копия.Домашнее задание: найдите в сети Internet примеры фракталов, встречающихся в природе
Список литературы
1. Мандельброт Б. Фрактальная геометрия природы. М.: Институт компьютерных исследований, 2002.
2. Федер Е. Фракталы. М.: Мир, 1991.
3. Штейнгауз Г. Математический калейдоскоп. – М.: Наука, 1981. 160 с.