Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку геометрии "Свойства равнобедренного треугольника"
Содержание
- 1. Презентация к уроку геометрии "Свойства равнобедренного треугольника"
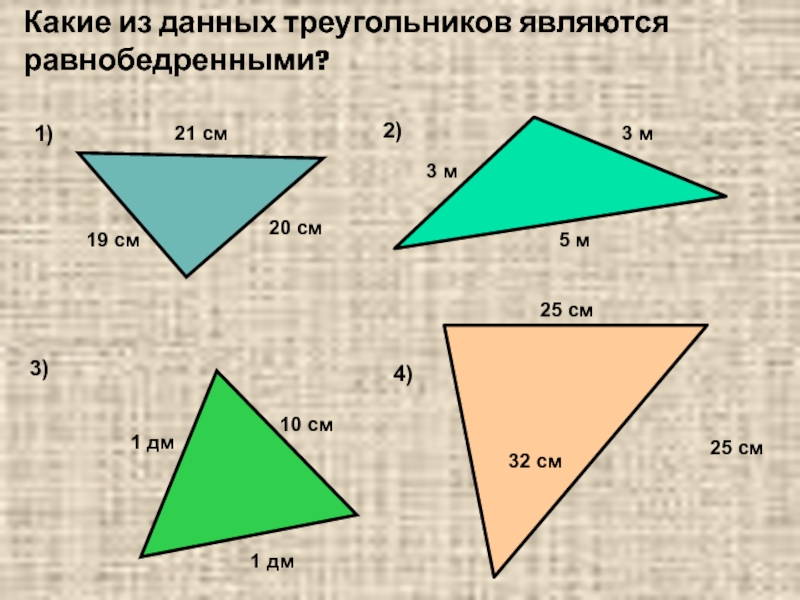
- 2. Какие из данных треугольников являются равнобедренными? 25
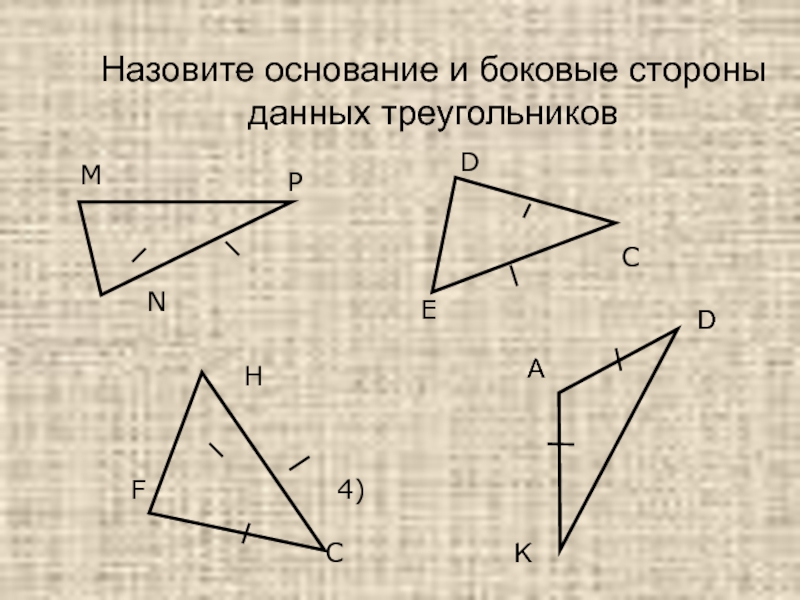
- 3. Назовите основание и боковые стороны данных треугольниковADK
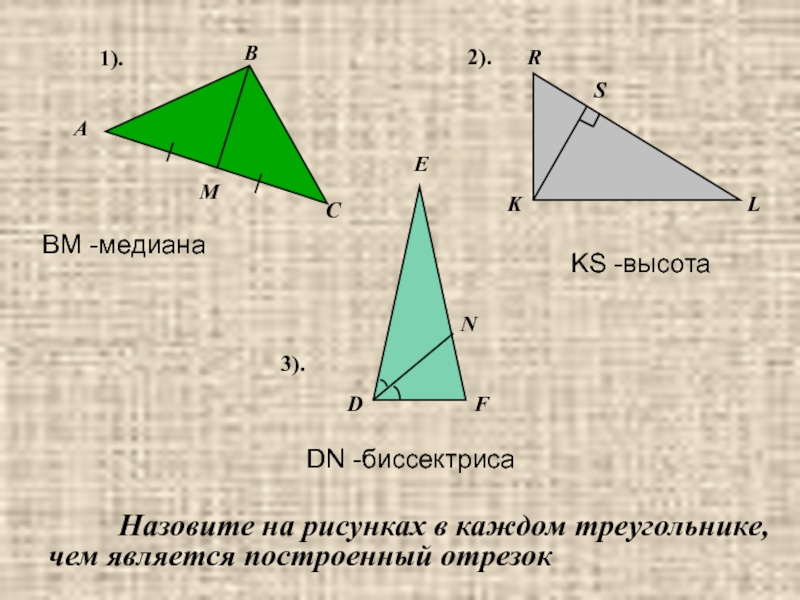
- 4. BACMENFDRSLK1).3).2). Назовите на
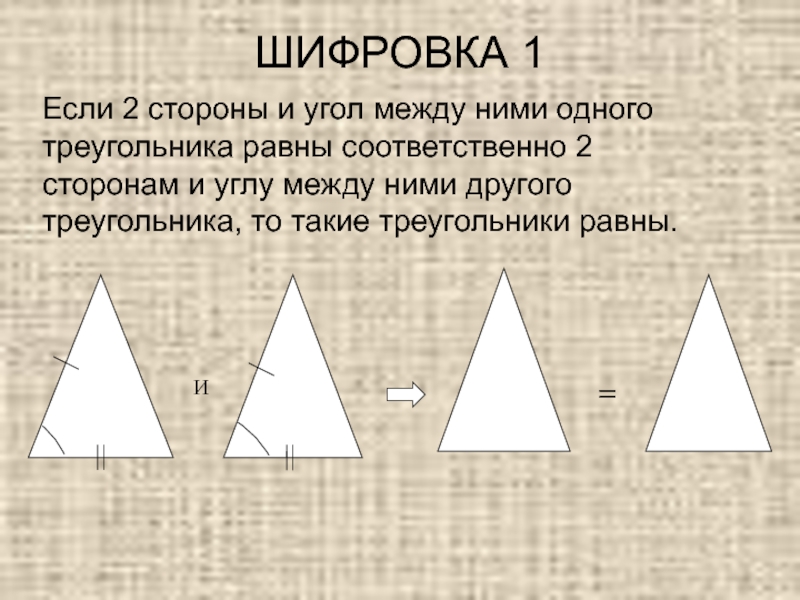
- 5. ШИФРОВКА 1И=Если 2 стороны и угол между
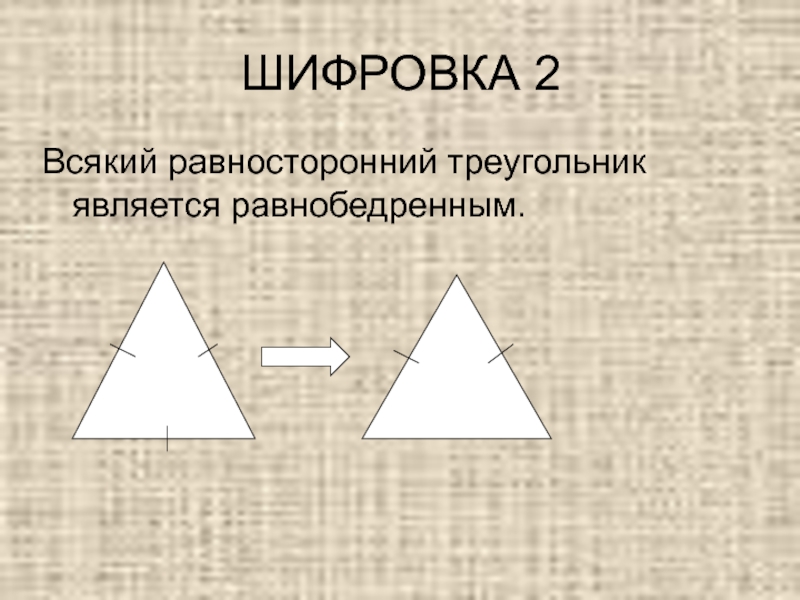
- 6. ШИФРОВКА 2Всякий равносторонний треугольник является равнобедренным.
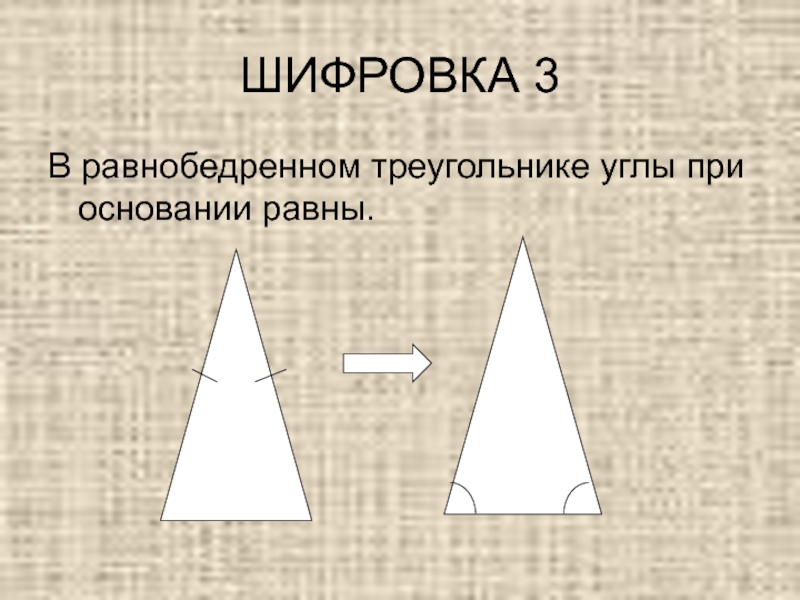
- 7. ШИФРОВКА 3В равнобедренном треугольнике углы при основании равны.
- 8. ВАСDДано:∆АВС, AB = АC,АD – биссектрисаДоказать:а) АD
- 9. АВСD
- 10. Справедливы так же утверждения:
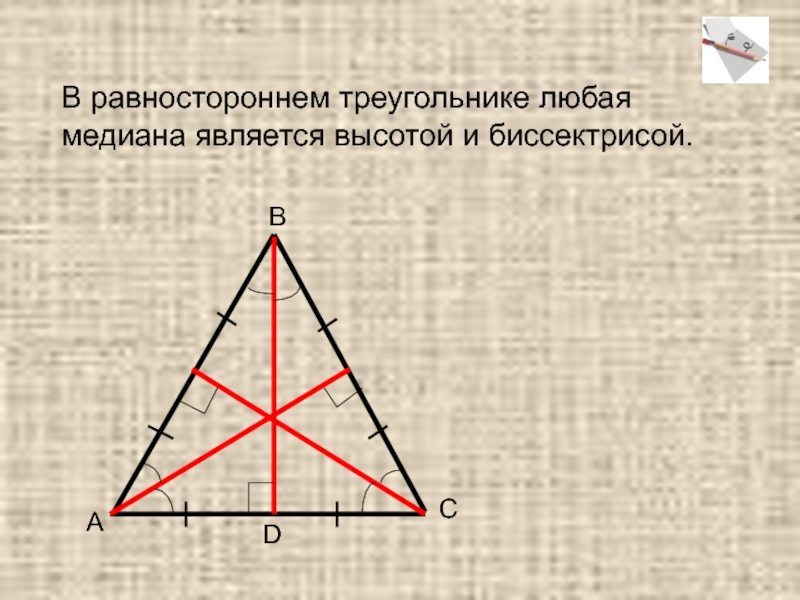
- 11. АВСDВ равностороннем треугольнике любая медиана является высотой и биссектрисой.
- 12. АВСК∆ АВС –равнобедренный,АС – основание, ВК –
- 13. Теоретический тест1.Медиана в равнобедренном треугольнике является его
- 14. Где в жизни встречаются равнобедренные треугольники?
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Домашнее задание:Пункт 18 (2);№ 111,№ 119;Творческое задание: Из 6 спичек получить 4 равносторонних треугольника.
- 19. Скачать презентанцию
Какие из данных треугольников являются равнобедренными? 25 см25 см32 см1 дм10 см1 дм19 см21 см20 см3 м3 м5 м1)2)3)4)
Слайды и текст этой презентации
Слайд 4
B
A
C
M
E
N
F
D
R
S
L
K
1).
3).
2).
Назовите на рисунках в каждом
треугольнике, чем является построенный отрезок
BM -медиана
KS -высота
DN -биссектриса
Слайд 5ШИФРОВКА 1
И
=
Если 2 стороны и угол между ними одного треугольника
равны соответственно 2 сторонам и углу между ними другого треугольника,
то такие треугольники равны.
Слайд 8
В
А
С
D
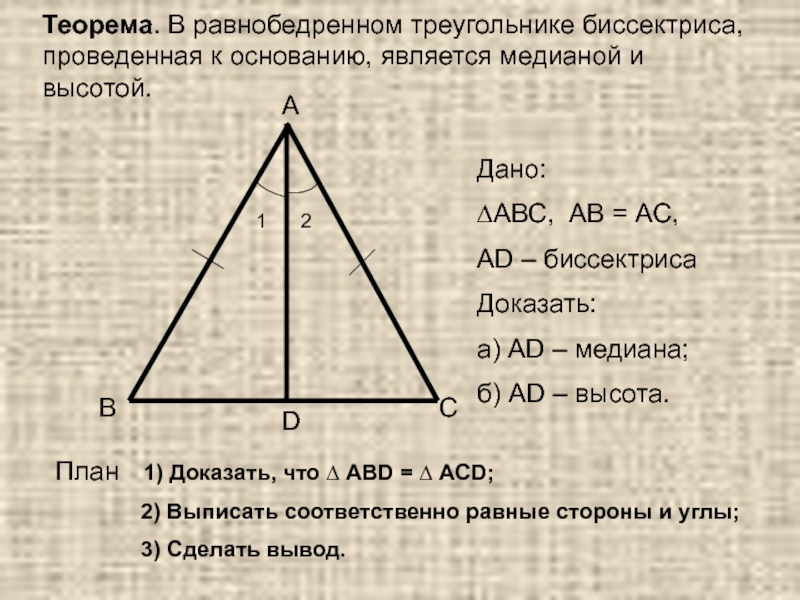
Дано:
∆АВС, AB = АC,
АD – биссектриса
Доказать:
а) АD – медиана;
б) АD
– высота.
1
2
План 1) Доказать, что ∆ АВD = ∆
АCD;2) Выписать соответственно равные стороны и углы;
3) Сделать вывод.
Теорема. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Слайд 9
А
В
С
D
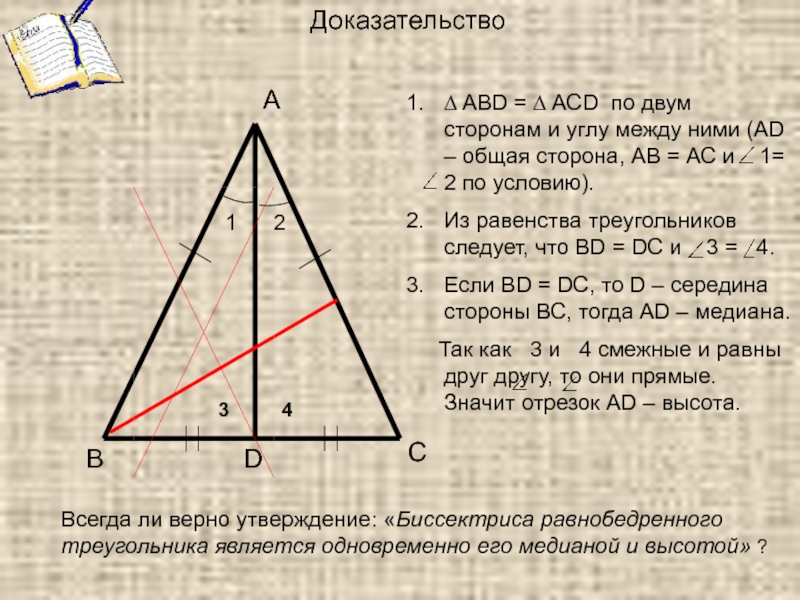
Доказательство
1
∆
ABD = ∆ ACD по двум сторонам и углу между ними (АD – общая сторона, АВ = АС и 1= 2 по условию).Из равенства треугольников следует, что ВD = DC и 3 = 4.
Если ВD = DC, то D – середина стороны ВС, тогда АD – медиана.
Так как 3 и 4 смежные и равны друг другу, то они прямые. Значит отрезок AD – высота.
3
4
Всегда ли верно утверждение: «Биссектриса равнобедренного треугольника является одновременно его медианой и высотой» ?
2
Слайд 10
Справедливы так же утверждения:
Высота равнобедренного треугольника, проведённая к основанию, является
медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведённая к основанию, является
высотой и биссектрисой.
Слайд 12А
В
С
К
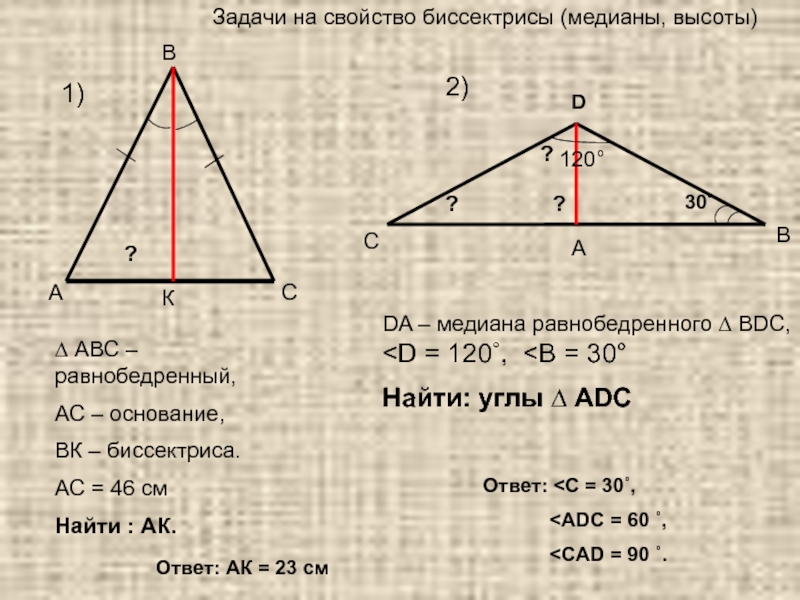
∆ АВС –равнобедренный,
АС – основание,
ВК – биссектриса.
АС = 46
см
Найти : АК.
D
А
С
В
DA – медиана равнобедренного ∆ ВDС,
Найти: углы ∆ АDС30˚
120°
?
?
?
Задачи на свойство биссектрисы (медианы, высоты)
?
Ответ: АК = 23 см
Ответ: 2) 1)
Слайд 13Теоретический тест
1.Медиана в равнобедренном треугольнике является его биссектрисой и высотой.
Это утверждение:
а) всегда
верно;б) может быть верно;
в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является медианой и биссектрисой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
5. Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая его медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Слайд 18Домашнее задание:
Пункт 18 (2);
№ 111,№ 119;
Творческое задание:
Из 6
спичек получить 4 равносторонних треугольника.
