Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к внеклассному мероприятию "Теорема Пифагора"
Содержание
- 1. Презентация к внеклассному мероприятию "Теорема Пифагора"
- 2. Слайд 2
- 3. Теорема Пифагораa – катетb – катетc -
- 4. Выбери правильный ответ:1. с2 = 82
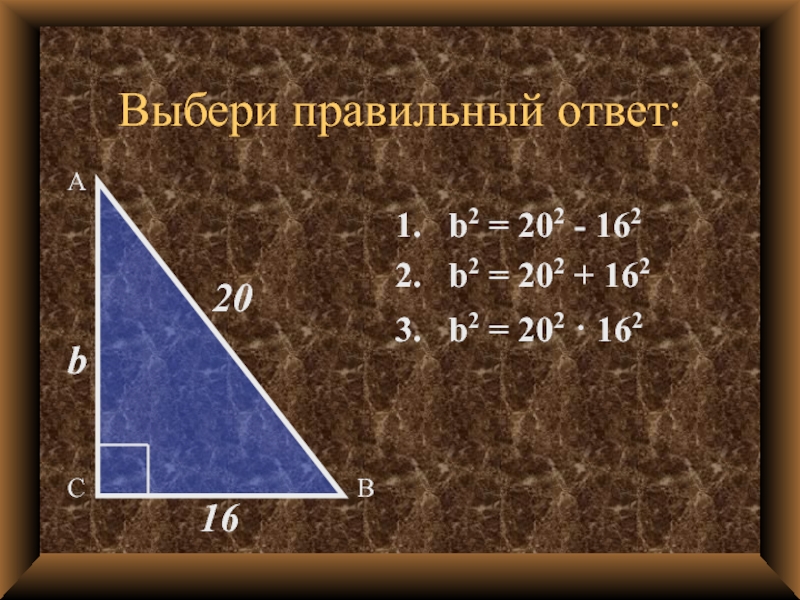
- 5. Выбери правильный ответ:16b20АВС1. b2 = 202
- 6. Задача:Найти неизвестную сторону треугольника34сВарианты ответов: 1. с = 17 2. с = 25 3. с = 5АСВ
- 7. Задача:Найти неизвестную сторону треугольника512сВарианты ответов: 1. с = 17 2. с = 13 3. с = 169АСВ
- 8. Задача:Определите, какой треугольник является прямоугольным?Варианты ответов: 1. 13
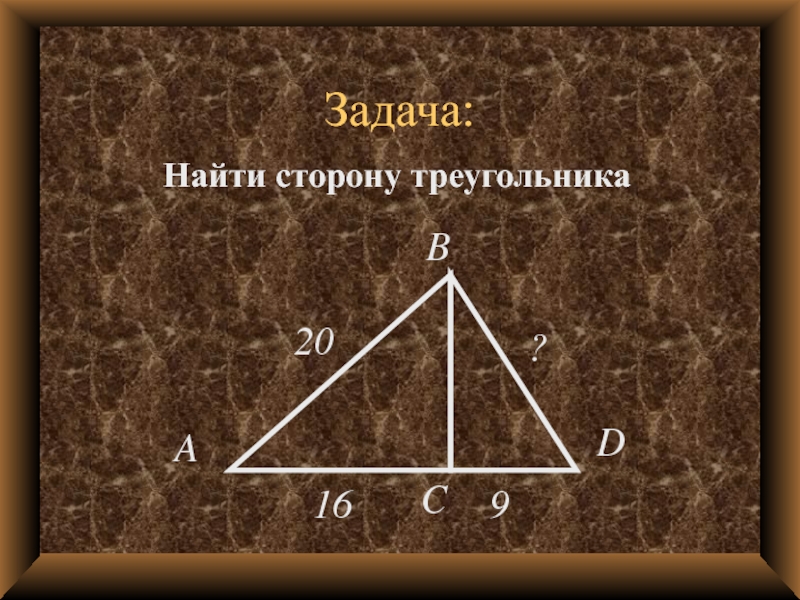
- 9. Задача:Найти сторону треугольника20169?ABCD
- 10. На берегу реки рос тополь одинокий.И вдруг
- 11. Случися некоему человеку к стене лестницу прибрати,
- 12. Над озером тихимС полфута размером Высился лотоса
- 13. Задача Имеется водоем со стороной в 1 чжан
- 14. Мы узнали что-то снова – Теорему Пифагора!И
- 15. Шаржи
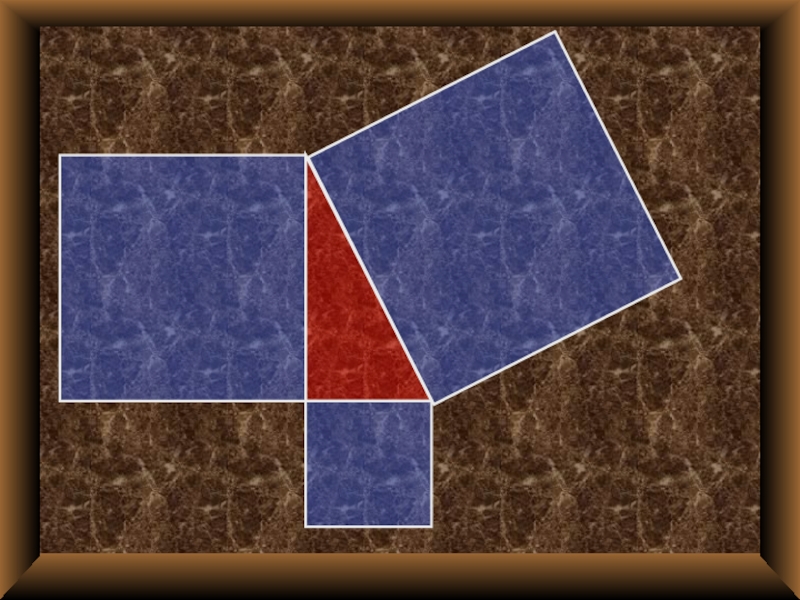
- 16. Из данного набора фигур составьте на сторонах треугольника квадраты гипотенузы и катетов.
- 17. Слайд 17
- 18. Наложите на квадрат гипотенузы квадраты катетов так, чтобы они совместились.
- 19. Слайд 19
- 20. ЗаключениеЕсли дан нам треугольникИ при том с
- 21. Скачать презентанцию
Теорема Пифагораa – катетb – катетc - гипотенузаc2 = a2 + b2Квадрат гипотенузы равен сумме квадратов катетов.
Слайды и текст этой презентации
Слайд 1Теорема Пифагора
Пребудет вечной истина так скоро
Ее познает слабый человек!
И ныне
теорема Пифагора
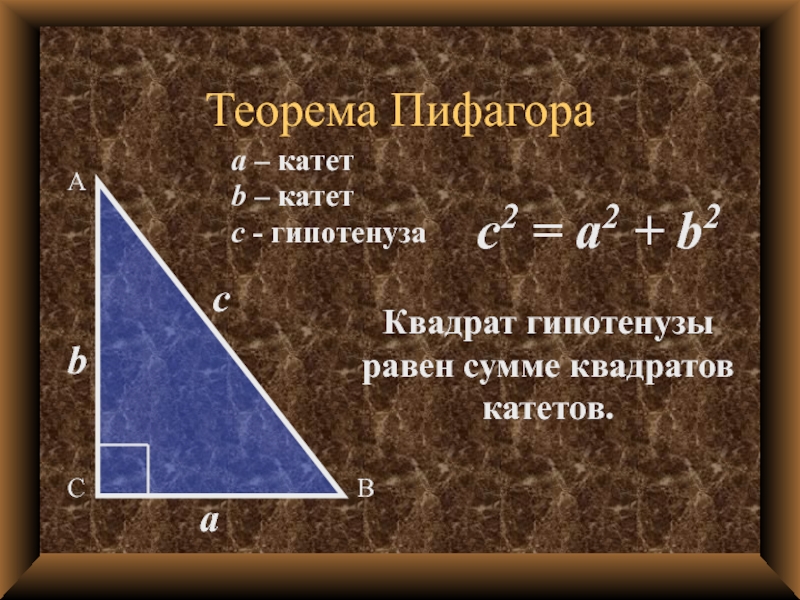
Слайд 3Теорема Пифагора
a – катет
b – катет
c - гипотенуза
c2 = a2
+ b2
Квадрат гипотенузы равен сумме квадратов катетов.
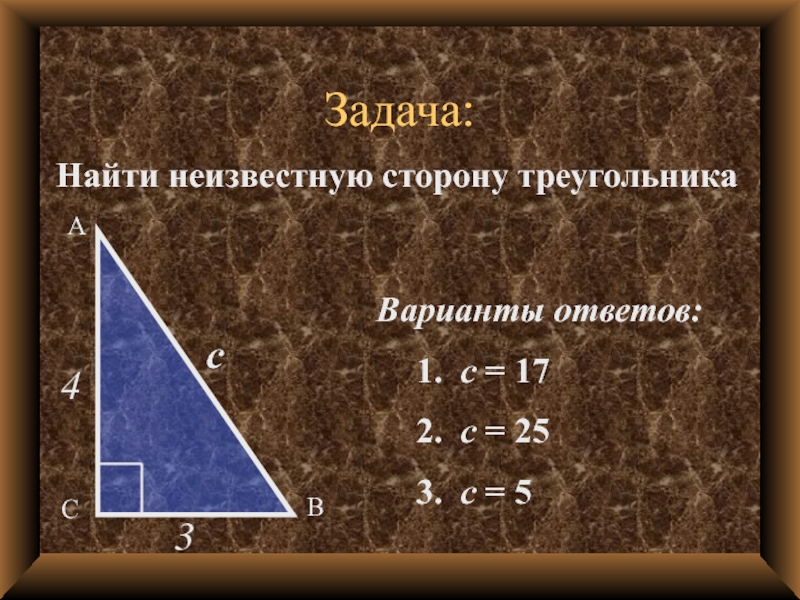
Слайд 6Задача:
Найти неизвестную сторону треугольника
3
4
с
Варианты ответов:
1. с = 17
2. с =
25
3. с = 5
А
С
В
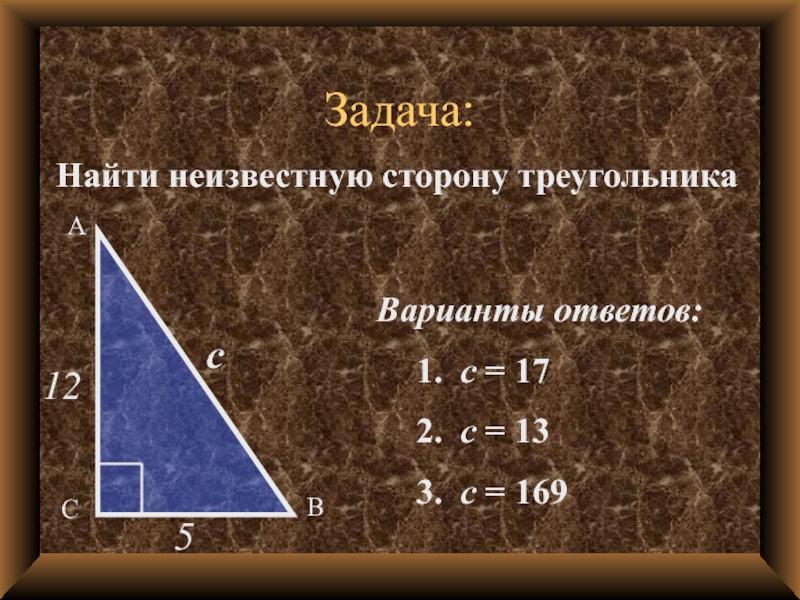
Слайд 7Задача:
Найти неизвестную сторону треугольника
5
12
с
Варианты ответов:
1. с = 17
2. с =
13
3. с = 169
А
С
В
Слайд 8Задача:
Определите, какой треугольник является прямоугольным?
Варианты ответов:
1. 13 м; 5
м; 12 м
2. 0,6 дм; 0,8 дм;
1,2 дм
Слайд 10На берегу реки рос тополь одинокий.
И вдруг ветра порыв его
ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его
угол прямой составлял.Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола.
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Тополь у реки
Слайд 11Случися некоему человеку к стене лестницу прибрати, стены же тоя
высота есть 117 стоп. И обретете лестницу долготью 125 стоп.
И ведати хочет, колико стол сея лестницы нижней конец от стены отстояти имать.Задача из учебника «Арифметика» Леонтия Магницкого
Слайд 12Над озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И
ветер порывом Отнёс его в сторону. Нет Боле цветка над водой. Нашёл же
рыбак его Ранней весною В двух футах от места, где рос. Итак, предложу я вопрос: “Как озера вода здесь глубока?”Древнеиндийская задача
Слайд 13Задача
Имеется водоем со стороной в 1 чжан = 10 чи.
В центре его растет камыш, который выступает над водой на
1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?
Слайд 14Мы узнали что-то снова –
Теорему Пифагора!
И её сквозь сотни
лет,
Продолжает знать весь свет.
Уж для этой теоремы
И не жалко даже
время.Хочешь снова повторять
Говорить и напевать:
Пифагоровы штаны
во все стороны равны!
Слайд 20Заключение
Если дан нам треугольник
И при том с прямым углом,
То квадрат
гипотенузы
Мы всегда легко найдем:
Суммы степеней находим
И таким простым путем
К
результату мы придем!
