Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия вокруг нас
Содержание
- 1. Симметрия вокруг нас
- 2. СИММЕТРИЯ ВОКРУГ НАС
- 3. Цели работы:Рассмотреть, как симметрия проявляется и используется
- 4. СИММЕТРИЯ ВОКРУГ НАС I.Симметрия. Общие положения.
- 5. «Симметрия» – (в перев. с греч.) совместная
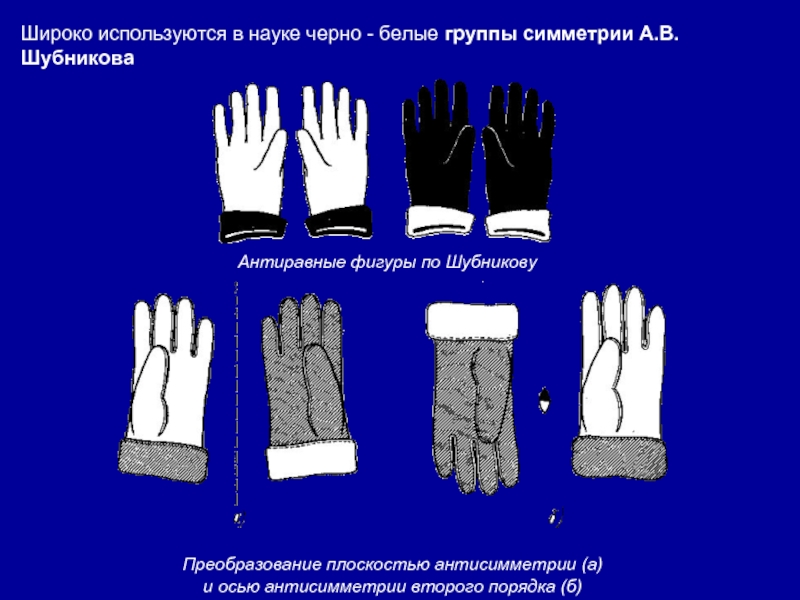
- 6. Широко используются в науке черно - белые группы симметрии А.В.Шубникова
- 7. Слайд 7
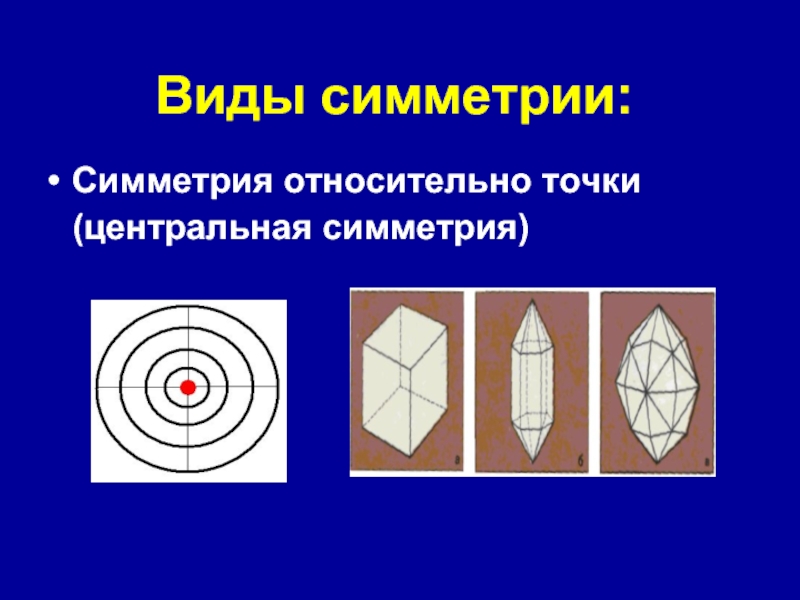
- 8. Виды симметрии: Симметрия относительно точки (центральная симметрия)
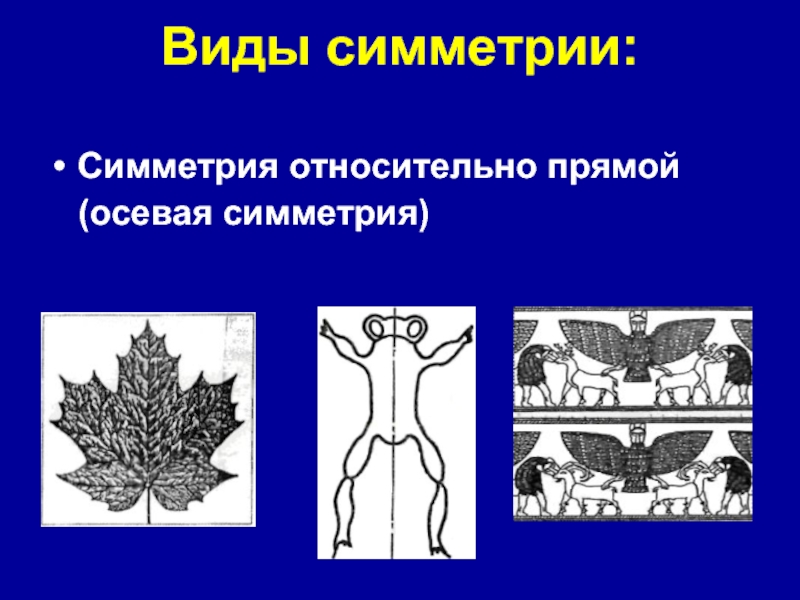
- 9. Виды симметрии: Симметрия относительно прямой (осевая симметрия)
- 10. Виды симметрии: Скользящая симметрия (переносная симметрия)С. Дали
- 11. Виды симметрии: Симметрия относительно плоскости (зеркальная симметрия)
- 12. Глава II. Единая Культура на принципах симметрии.
- 13. Симметрия в литературеПОЭТУ4
- 14. Симметрия в литературе
- 15. Симметрия в живописи
- 16. Симметрия в живописи
- 17. Симметрия в живописи
- 18. Симметрия вокруг нас
- 19. Симметрия вокруг нас
- 20. Симметрия вокруг насПирамида Чичен Ица
- 21. Симметрия вокруг насЗАЛ ВЕЛИКОГО БУДДЫ 752 г.,
- 22. Симметрия вокруг насЭЙФЕЛЕВА БАШНЯ1889 г., ФранцияДерзновенное сооружение,
- 23. Симметрия вокруг нас
- 24. Функции и их графикиСимметрия используется при работе с понятиями:Четная или нечетная функция. Обратная функция.
- 25. 4)Пример 7. Укажите график нечетной функции. Решение.
- 26. Пример 19. По графику функции f
- 27. ПалиндроматикаА РОЗА УПАЛА НА ЛАПУ АЗОРА. 42+35=53+24
- 28. СИММЕТРИЯ ВОКРУГ НАС
- 29. СИММЕТРИЯ ВОКРУГ НАС
- 30. СИММЕТРИЯ ВОКРУГ НАС
- 31. СИММЕТРИЯ ВОКРУГ НАС
- 32. СИММЕТРИЯ ВОКРУГ НАС
- 33. СИММЕТРИЯ ВОКРУГ НАС
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1СИММЕТРИЯ ВОКРУГ НАС
Выполнила:
Ученица МОУ СОШ №7
Папоян Нарине Норайровна
Руководитель:
учитель математики
Калачева Наталья
Анатольевна
Слайд 3Цели работы:
Рассмотреть, как симметрия проявляется и используется в окружающем нас
мире.
Рассмотреть, как симметрия используется в школьном курсе алгебры.
Задачи:
Изучить литературу
по теме исследования.Выделить целесообразность изучения темы.
Выделить основные направления применения симметрии в творчестве человека.
Выделить вопросы школьного курса алгебры, в которых
используется симметрия.
Рассмотреть, как симметрия используется при решении задач.
Слайд 4СИММЕТРИЯ ВОКРУГ НАС
I.Симметрия. Общие положения.
II. Единая
Культура на принципах симметрии.
III. Симметрия в школьном
курсе алгебры.Приложения
Слайд 5«Симметрия» – (в перев. с греч.) совместная мера, соразмерность.
Симметрия - в широком или узком смысле, в зависимости от
того, как вы определяете значение этого понятия, - является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство.Г. Вейль
I.Симметрия. Общие положения.
С. Дали
Слайд 12Глава II. Единая Культура на принципах симметрии.
С симметрией в природе мы встречаемся не менее часто, чем
в человеческом творчестве. "Параллельность" мира искусства и науки, в первую очередь, проявляется в единстве организации структуры произведения искусства и объекта исследования науки, а это должно сказаться на выборе общего языка для описания структур. Таким языком, на наш взгляд, является язык симметрии.§1. Симметрия в литературе
§2. Симметрия в живописи
Слайд 20Симметрия вокруг нас
Пирамида Чичен Ица
Пирамида Чичен
Ица (до 800 н.э) Юкатан Пенинсула, Мексика, самый знаменитый храм
Майя, служил как политический и экономический центр цивилизации Майя. Целый комплекс различных сооружений - Кукулкан-пирамиды, храм Чак Мол, Зал Тысячи колон и Игровое поле для пленных (их и сегодня можно посетить) – наглядно демонстрирует экстраординарный взгляд на архитектуру и композицию. Пирамида, построенная последней, является самым значительным сооружением среди храмов цивилизации Майя.Слайд 21Симметрия вокруг нас
ЗАЛ ВЕЛИКОГО БУДДЫ
752 г., Япония
Дайбуцудэн, или Зал
Великого Будды, в монастыре Тодайдзи, - это самое большое деревянное
здание в мире, хотя сегодня оно составляет всего лишь две трети от своей первоначальной величины. Множество раз оно горело, и множество раз его восстанавливали. Сегодня оно занимает площадь 58 X 51 метр, а по высоте равно 49 метрам. Зал был построен в VIII веке по приказу императора Шому, и в нем находится одна из самых больших бронзовых статуй мира.Слайд 22Симметрия вокруг нас
ЭЙФЕЛЕВА БАШНЯ
1889 г., Франция
Дерзновенное сооружение, вершина и торжество
технической мысли XIX столетия, прославившееся во всем мире как эмблема
ПарижаВ горизонтальной проекции Эйфелева башня опирается на квадрат площадью в 1,6 гектара. Вместе с антенной ее высота составляет 320,75 метра, она весит 8600 тонн, и, как уверяют специалисты, в процессе ее постройки было заклепано 2,5 миллиона заклепок. 12 000 деталей для башни изготовлялись по точнейшим чертежам. Самая высокая по тем временам башня в мире была смонтирована 250 рабочими в поразительно короткий срок.
Слайд 24Функции и их графики
Симметрия используется при работе с понятиями:
Четная или
нечетная функция.
Обратная функция.
Слайд 25
4)
Пример 7. Укажите график нечетной функции.
Решение. График нечетной функции симметричен
относительно начала координат. На рисунке 2) изображен именно такой график.
Ответ:
2.Слайд 26
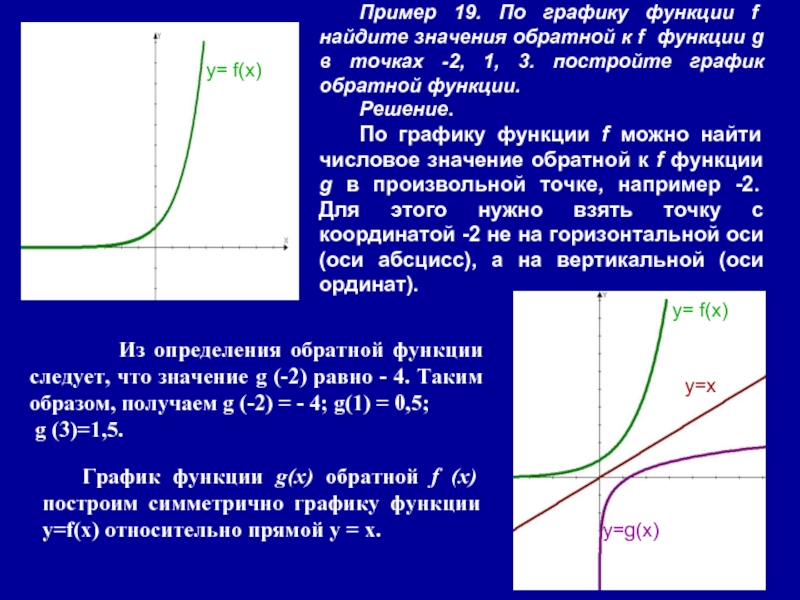
Пример 19. По графику функции f найдите значения обратной к
f функции g в точках -2, 1, 3. постройте график
обратной функции.Решение.
По графику функции f можно найти числовое значение обратной к f функции g в произвольной точке, например -2. Для этого нужно взять точку с координатой -2 не на горизонтальной оси (оси абсцисс), а на вертикальной (оси ординат).
Из определения обратной функции следует, что значение g (-2) равно - 4. Таким образом, получаем g (-2) = - 4; g(1) = 0,5;
g (3)=1,5.
,
,
График функции g(х) обратной f (х) построим симметрично графику функции у=f(x) относительно прямой у = х.
.
у= f(x)
у= f(x)
y=x
y=g(x)
Слайд 27Палиндроматика
А РОЗА УПАЛА НА ЛАПУ АЗОРА.
42+35=53+24
41-32=23-14
63·48=84·36
82 _ 2841 ¯ 14