Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Измерение по топографической карте
Содержание
- 1. Измерение по топографической карте
- 2. Цели занятия:Изучить понятия масштабов;Научиться определять азимуты и
- 3. Учебные вопросы:1. Численный и линейный масштаб карты.
- 4. Литература:Тактико-специальная подготовка: Учебник. Ч. 1, переработанное и
- 5. Масштабом называют отношение длины линий на карте
- 6. Масштаб:
- 7. Численный масштаб: ПРАВИЛО 1: Если в правой
- 8. Топографические карты изготовляются в следующих основных
- 9. ПРАВИЛО 2: Чем меньше степень уменьшения
- 10. Пример: Для того, чтобы определить расстояние
- 11. Линейный масштаб:Линейный масштаб — это графическое изображение
- 12. Измерение по карте С помощью линейного
- 13. При измерении расстояний по ломаным линиям необходимо
- 14. Измерение линий на картеВеличину «шага» выбирают в
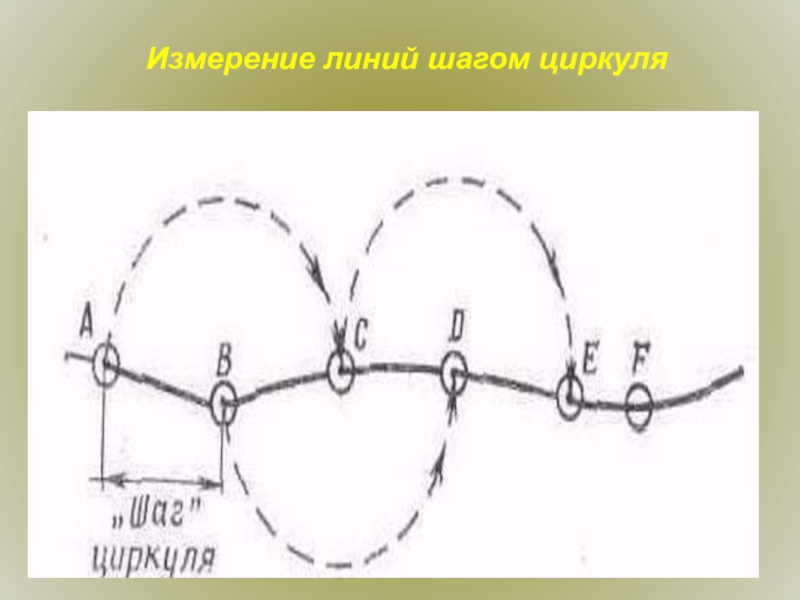
- 15. Измерение линий шагом циркуля
- 16. Поперечный масштабДля более точного измерения и откладывания
- 17. Поперечный масштаб
- 18. Измерение линий наращиванием раствора циркуля
- 19. Курвиметр Курвиметр — это прибор для
- 20. При движении колесика стрелка показывает путь, проходимый
- 21. Координатами называются угловые или линейные величины, определяющие
- 22. 1. Географические координаты Географическими координатами какой-либо точки, например М, являются ее широта В и долгота L.
- 23. Широта точки - угол, составленный плоскостью экватора
- 24. Долгота точки - двугранный угол между плоскостью
- 25. Шкалы географических координат и километровая сетка на
- 26. Слайд 26
- 27. Географическая сетка и обозначение километровых линий на карте масштаба 1:500 000
- 28. Система плоских прямоугольных координат шестиградусной зоны За
- 29. Оси координат делят зону на четверти, счет
- 30. Положение какой-либо точки, например М, указывается ее расстоянием от осей координат: абсциссой х и ординатой у.
- 31. Принцип оцифровки километровых линий координатной сетки в
- 32. Слайд 32
- 33. Обозначение координатной сетки смежной зоны за рамки
- 34. Слайд 34
- 35. Определение по карте прямоугольных координат точки (А)
- 36. Истинный азимут (А), магнитный азимут (Ам) и дирекционный угол (α )
- 37. Дирекционный угол:Дирекционным углом (α) какого-либо направления называется
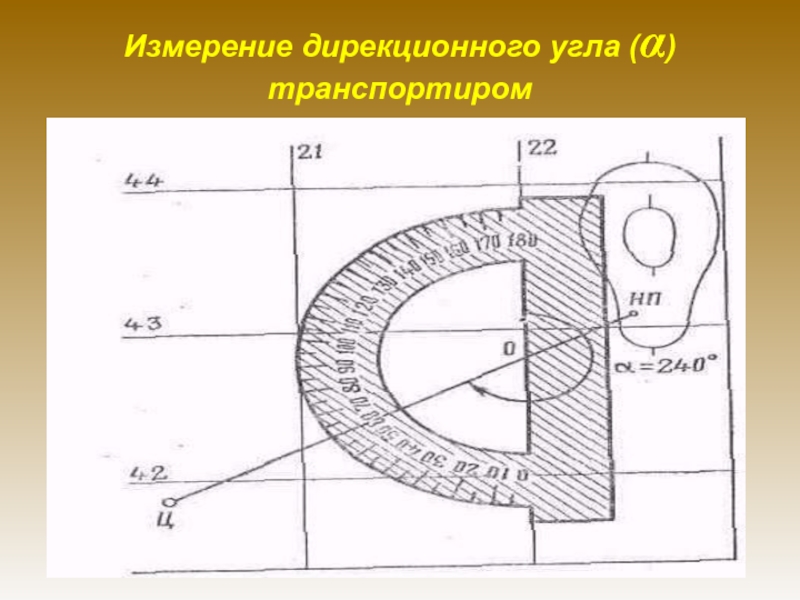
- 38. Измерение дирекционного угла (α) транспортиром
- 39. Истинный азимут: Истинным или географическим азимутом А направления
- 40. Магнитный азимут:Магнитным азимутом Ам направления называется горизонтальный
- 41. Магнитный меридиан: При ориентировании на местности за направление
- 42. Магнитное склонение (δ - дельта): Так как истинный
- 43. Схема магнитного склонения, сближения меридианов и поправки направления
- 44. Сближение меридианов (γ - гамма) : Между вертикальной
- 45. Определение поправки для перехода от дирекционного угла (а) к магнитному азимуту (Ам) и обратно
- 46. Формула для вычисления магнитного азимута: Ам = α – ((δ) – (γ))
- 47. 3. Определение расстояний и линейных размеров наблюдаемых объектов.
- 48. 3.1 Простейшие способы приближенного определения расстояний:1.Глазомер;2.По измеренным
- 49. 1. Глазомер — основной, самый простой и
- 50. В процессе такой тренировки основное внимание надо
- 51. — ярко освещенные предметы кажутся ближе слабо
- 52. в) чем меньше промежуточных предметов находится между
- 53. г) при наблюдении снизу вверх, от подошвы
- 54. Глазомерная оценка расстояний может облегчаться и контролироваться
- 55. Точность глазомера зависит от натренированности наблюдателя, от
- 56. Слайд 56
- 57. 2. Определение расстояний по измеренным угловым размерам
- 58. На рис. показано, что дуга АК=Т, стягивающая
- 59. Для малых углов, не превышающих 300 тысячных
- 60. Для малых углов, не превышающих 300 тысячных
- 61. Решая пропорцию относительно В или Д, получим
- 62. Определение расстояний по угловым размерам предметов дает
- 63. Простейшие способы измерения углов. Измерение углов полевым
- 64. Так, например, пулемет противника расположен правее ориентира (дерева) на угол 0-55.
- 65. Измерение углов с помощью линейки. При отсутствии бинокля
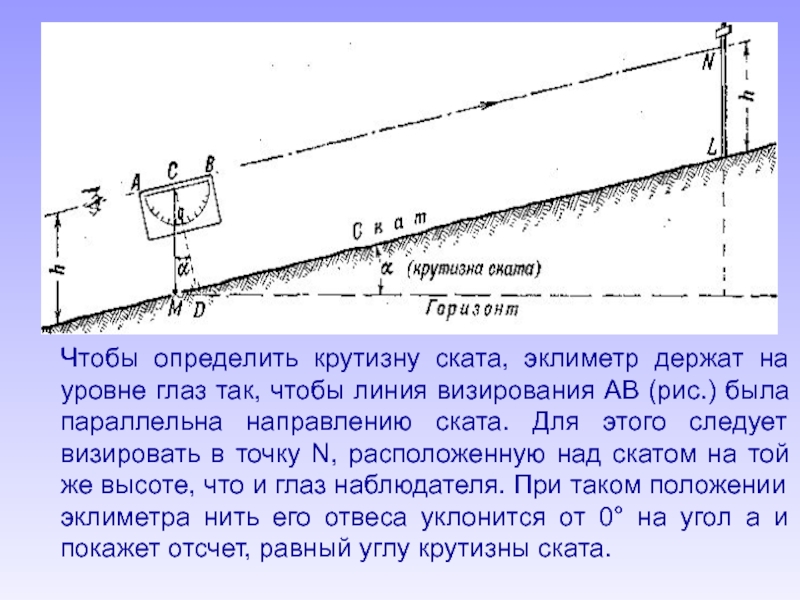
- 66. Если линейку держать перед собой на расстоянии
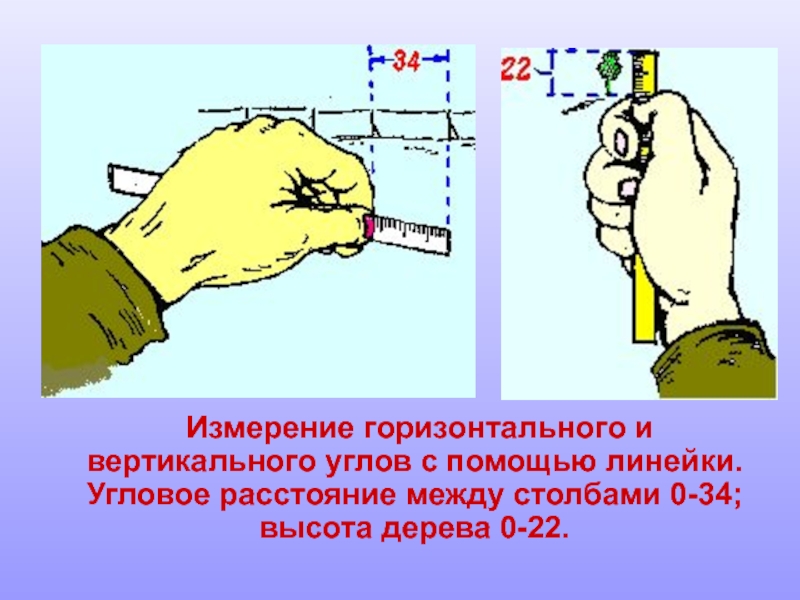
- 67. Измерение горизонтального и вертикального углов с помощью
- 68. С помощью линейки удобно измерять малые углы
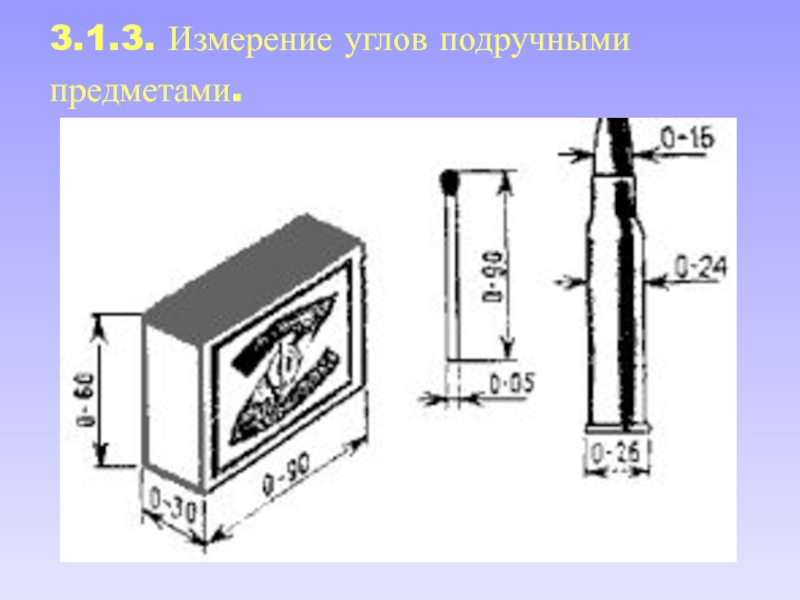
- 69. 3.1.3. Измерение углов подручными предметами.
- 70. Вместо линейки с делениями можно использовать палец,
- 71. 3. Измерение расстояний шагами. В боевой обстановке
- 72. Чтобы повысить точность измерения расстояний шагами, необходимо:а)
- 73. При измерении расстояний шаги считаются парами (обычно
- 74. Принимая среднюю длину шага за 0,75 м,
- 75. 4. Определение расстояний по времени движения. Этот
- 76. 5. Определение расстояний по звуку и вспышке
- 77. Для приближенного определения расстояний можно считать, что
- 78. При отсутствии часов отсчитывать секунды можно путем
- 79. При более точных определениях расстояний время отсчитывается
- 80. 6. Определение расстояний на слух. Ночью и
- 81. Слайд 81
- 82. Приведенные в таблицах данные приближенны и непостоянны.
- 83. К основным из этих факторов относятся: направление
- 84. Слышимость усиливается, когда ветер дует со стороны
- 85. Звук поглощается, т. е. становится слабее, в
- 86. 3.2 Определение крутизны скатов 1. Оценка на
- 87. Более точные результаты получаются, если, зайдя сбоку
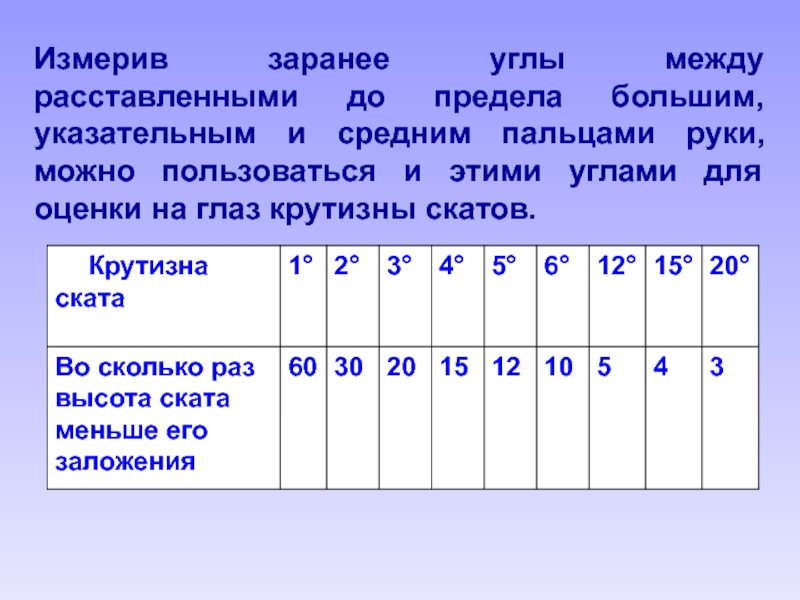
- 88. Измерив заранее углы между расставленными до предела
- 89. 2. Сравнение высоты ската с его заложением.
- 90. Для определения крутизны по этому способу надо:
- 91. б) оценить на глаз или с помощью
- 92. 3. Промер шагами. Крутизна ската этим способом
- 93. На продолжении линии визирования замечают на скате
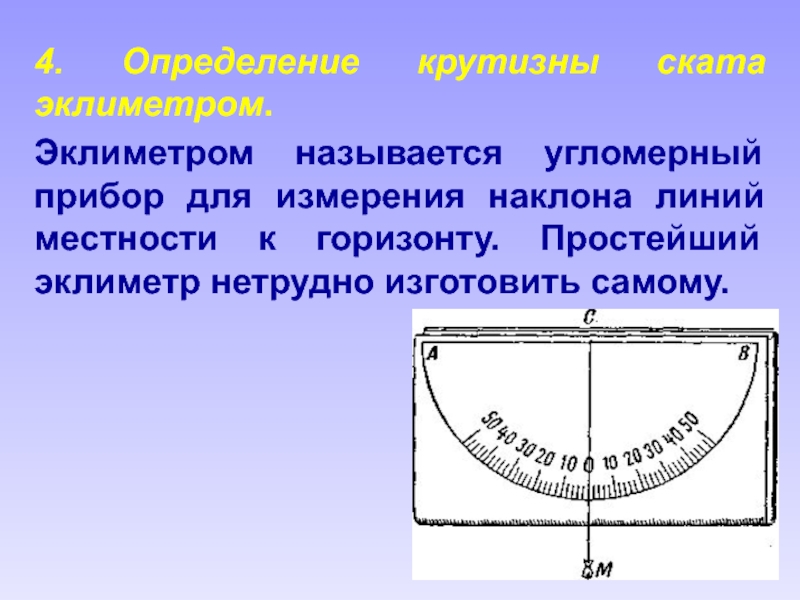
- 94. 4. Определение крутизны ската эклиметром. Эклиметром называется
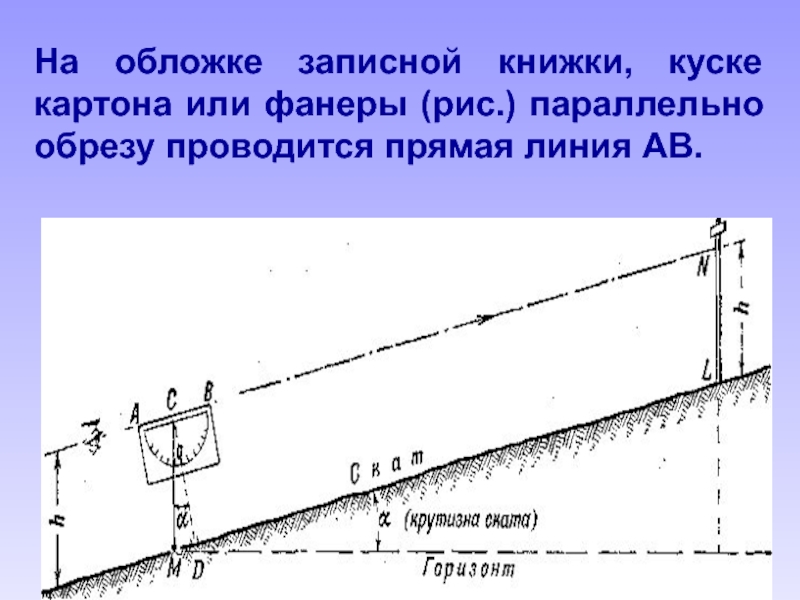
- 95. На обложке записной книжки, куске картона или фанеры (рис.) параллельно обрезу проводится прямая линия АВ.
- 96. Из середины С этой линии описывается полуокружность
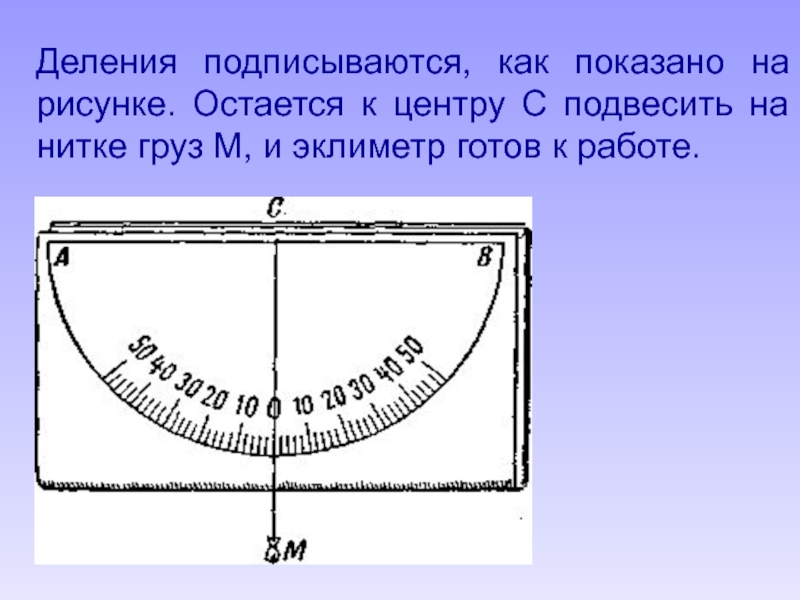
- 97. Деления подписываются, как показано на рисунке. Остается
- 98. Чтобы определить крутизну ската, эклиметр держат на
- 99. Скачать презентанцию
Цели занятия:Изучить понятия масштабов;Научиться определять азимуты и дирекционные углы;Приобрести навыки простейших измерений по карте и их применения при решении практических задач.
Слайды и текст этой презентации
Слайд 2Цели занятия:
Изучить понятия масштабов;
Научиться определять азимуты и дирекционные углы;
Приобрести навыки
Слайд 3Учебные вопросы:
1. Численный и линейный масштаб карты. Измерение расстояний и
площадей по карте различными способами.
2. Определение на карте координат точек
местности, азимутов и дирекционных углов.3. Определение расстояний и линейных размеров наблюдаемых объектов.
Слайд 4Литература:
Тактико-специальная подготовка: Учебник. Ч. 1, переработанное и дополненное. – М.:
ДГСК МВД России, 2011. – 368 с.
Пресняков, В.В. Военная
топография: учебник / В.В. Пресняков, Е.П. Андриясов., под ред. А.В.Маркеленко. – Феникс, 2008.– 265с.Сологуб, Ю.И. Специальная топография в ОВД: учеб. пособие/Ю.И. Сологуб, Р.В. Павленков, А.В. Галыгин. – Нижний Новгород: Нижегородская академия МВД России, 2010.–129с.
Слайд 5Масштабом называют отношение длины линий на карте к длине соответствующих
им линий на местности. Масштаб выражается в виде отношения двух
чисел и на картах указывается численным значением и линейным.1. Численный и линейный масштаб карты. Измерение расстояний и площадей по карте различными способами.
Слайд 7Численный масштаб:
ПРАВИЛО 1:
Если в правой части указанного масштаба,
отношение зачеркнуть два последних нуля, то остается число, которое покажет,
сколько метров на местности соответствует одному сантиметру на карте (величина масштаба). Если в правой части отношение зачеркнуть пять нулей, то остается число, которое покажет, сколько километров на местности соответствует одному сантиметру на карте.
Слайд 8 Топографические карты изготовляются в следующих основных масштабах:
1 : 25000;
1 : 50000;
1 : 100000;
1 : 200000;
1
: 500000; 1 : 1000000.
ОВД работают с масштабами:
1 : 25000;
1 : 50000;
Слайд 9ПРАВИЛО 2:
Чем меньше степень уменьшения (меньше цифровое значение масштаба),
тем крупнее масштаб карты, а следовательно, более детально изображена данная
местность.И, наоборот, на мелкомасштабных картах многие детали местности отсутствуют.
Слайд 10Пример: Для того, чтобы определить расстояние между какими-либо пунктами по
карте, следует измерить это расстояние в сантиметрах и умножить на
величину масштаба.На карте масштаба 1 : 50 000 измерено расстояние 3,4 см — значит, буквально на местности расстояние будет:
500 × 3,4 = 1700 м.
Слайд 11Линейный масштаб:
Линейный масштаб — это графическое изображение численного масштаба в
виде прямой линии с делениями для отсчета расстояний.
Слайд 12Измерение по карте
С помощью линейного масштаба расстояния по
карте можно определять без вычислений. Для этого следует
циркулем, линейкой или полоской бумаги измерить расстояниемежду данными точками на карте и, приложив циркуль (линейку, полоску бумаги) с этим расстоянием к линейному масштабу, прочитать какое расстояние на местности.
Слайд 13При измерении расстояний по ломаным линиям необходимо измерять общую длину
всех отрезков и затем пользоваться численным или линейным масштабом. При
измерении извилистых линий можно взять раствор циркуля, соответствующий наименьшему изгибу линии, и измерить им расстояние или использовать курвиметр.
Слайд 14Измерение линий на карте
Величину «шага» выбирают в зависимости от извилистости
линии: от 4—5 см — при измерении кривых с плавными
закруглениями, до 1—2 см—при измерении линий с большим числом резких поворотов. Последние более удобно измерять так, как показано на рис. Ломаная АВСDЕF равна по длине конечному раствору циркуля А4F, величину которого определяют по масштабной линейке.
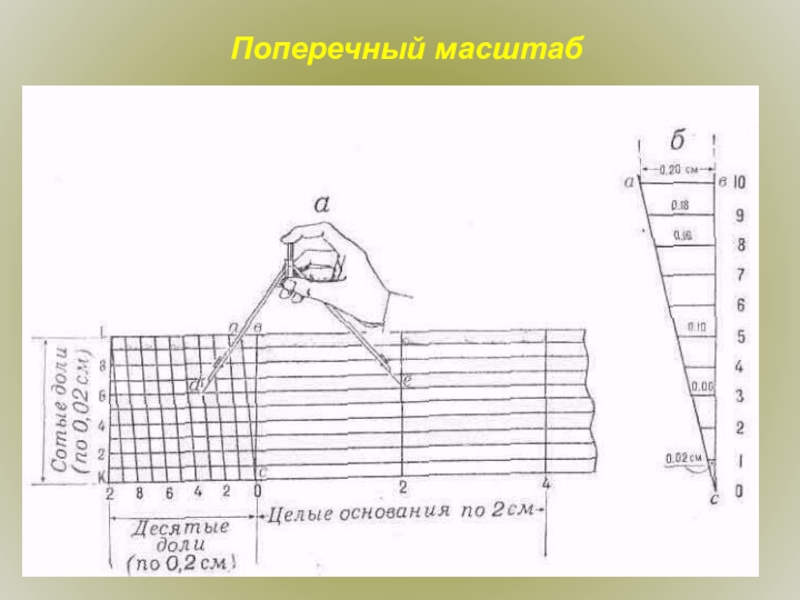
Слайд 16Поперечный масштаб
Для более точного измерения и откладывания расстояний по карте,
например при подготовке к ориентированию на местности с помощью навигационной
аппаратуры или при определении исходных данных для стрельбы, применяют поперечный масштаб - специальный график, награвированный на металлической линейке (рис.). Карта для таких измерений должна быть хорошо расправлена и прикреплена к какой-либо жесткой основе (планшету).
Слайд 19Курвиметр
Курвиметр — это прибор для измерения расстояний по
карте.
Поставив колесико на начало линии, передвигают его по измеряемому
пути. 
Слайд 20При движении колесика стрелка показывает путь, проходимый колесиком в сантиметрах.
Зная расстояние в сантиметрах на карте и масштаб карты, легко
вычислить расстояние на местности.На новых курвиметрах стрелка показывает расстояние на местности в зависимости от масштаба карты, для карт масштабов 1 : 25000 - 4,2 км; 1 : 50000 - 8,5 км; 1 :100000 -17 км.
Слайд 21
Координатами называются угловые или линейные величины, определяющие положение точек на
какой-либо поверхности или в пространстве.
2. Определение на карте координат точек
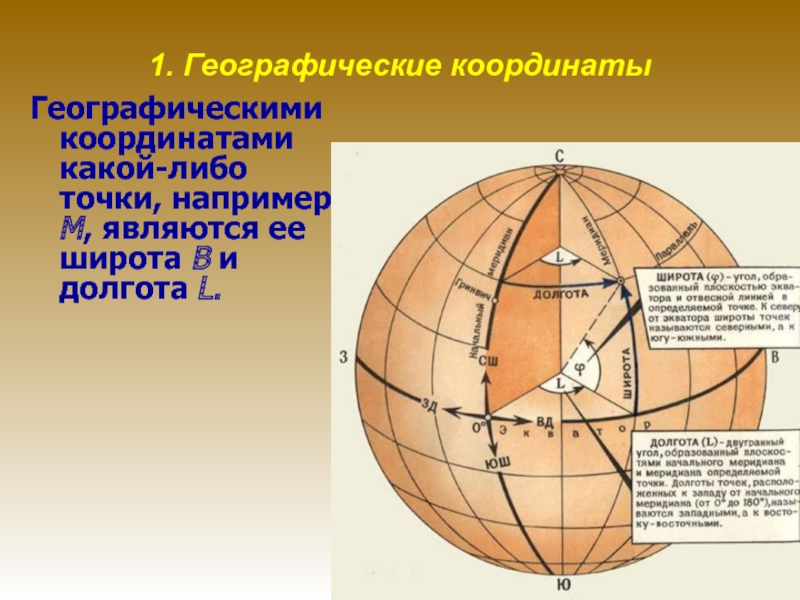
местности, азимутов и дирекционных углов.
Слайд 221. Географические координаты
Географическими координатами какой-либо точки, например М, являются
ее широта В и долгота L.
Слайд 23Широта точки - угол, составленный плоскостью экватора и нормалью к
поверхности земного эллипсоида, проходящей через данную точку. Счет широт ведется
по дуге меридиана в обе стороны от экватора, от 0 до 90°. Широты точек северного полушария называются северными, а южного - южными.
Слайд 24Долгота точки - двугранный угол между плоскостью начального (Гринвичского) меридиана
и плоскостью меридиана данной точки. Счет долгот ведется по дуге
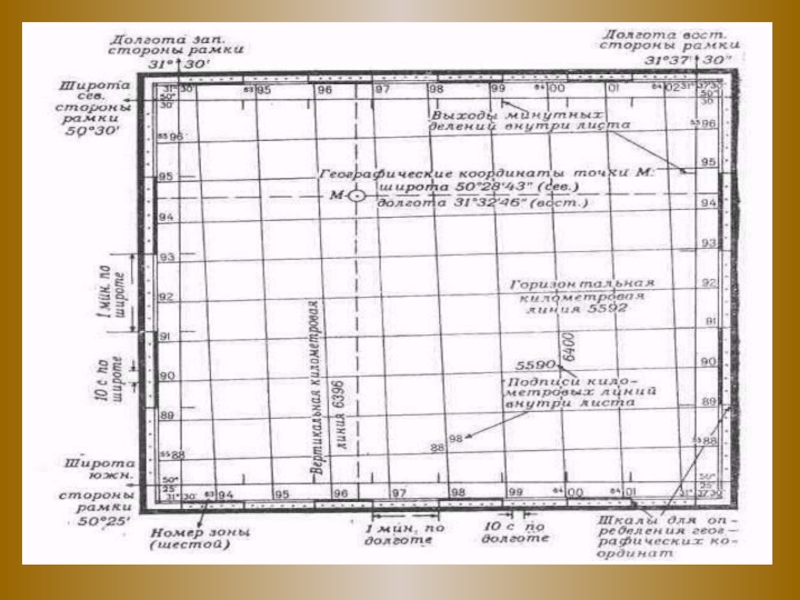
экватора или параллели в обе стороны от начального меридиана, от 0 до 180°. Долготы точек, расположенных к востоку от Гринвича до 180°, называются восточными, а к западу - западными.
Слайд 25Шкалы географических координат и километровая сетка на листе карты (масштаба
1:25 000)
При определении географических координат по карте масштаба 1:500 000
или 1:1 000 000 вместо шкал на рамке карты линейку прикладывают к одноименным делениям (или их долям), находящимся на меридианах (параллелях), ближайших к определяемой точке.
Слайд 28Система плоских прямоугольных координат шестиградусной зоны
За оси координат в
этой системе приняты изображение осевого меридиана координатной зоны - ось
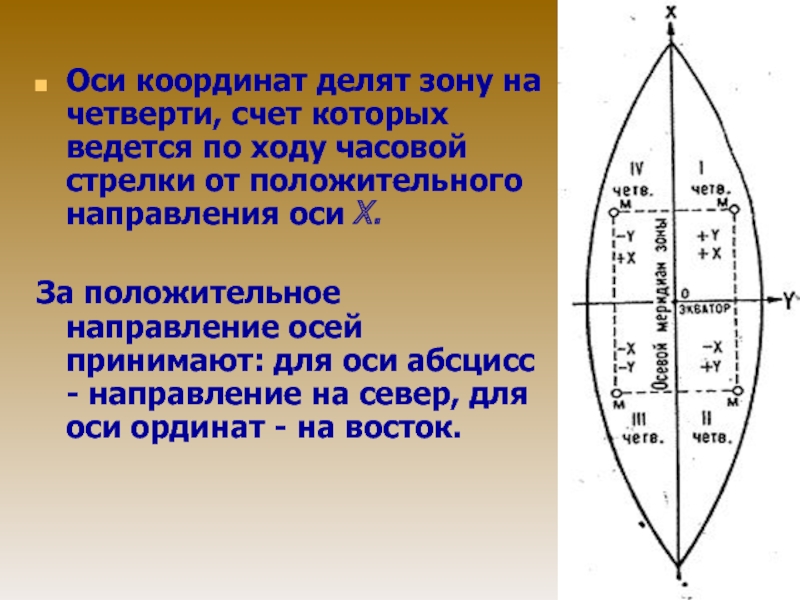
абсцисс Х и изображение экватора - ось ординат Y.
Слайд 29Оси координат делят зону на четверти, счет которых ведется по
ходу часовой стрелки от положительного направления оси X.
За положительное
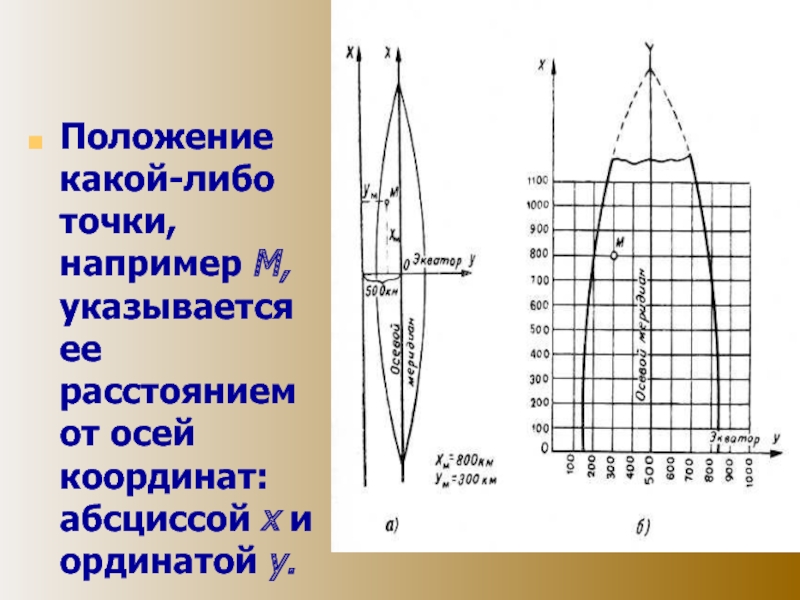
направление осей принимают: для оси абсцисс - направление на север, для оси ординат - на восток.
Слайд 30Положение какой-либо точки, например М, указывается ее расстоянием от осей
координат: абсциссой х и ординатой у.
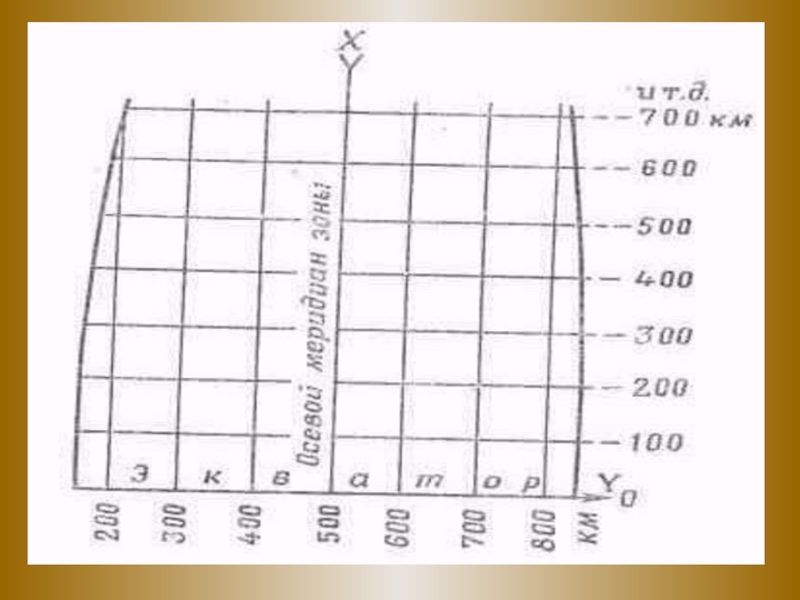
Слайд 31Принцип оцифровки километровых линий координатной сетки в пределах зоны
Линии сетки
проведены параллельно осям координат через 2 см на картах масштабов
1:50 000 - 1:500 000 (на карте масштаба 1:500 000 линии прямоугольной координатной сетки внутри листов не прочерчены, а показаны лишь их выходы на рамках (рис. 36)) и через 4 см на карте масштаба 1:25 000, что соответствует целому числу километров на местности. Поэтому прямоугольную координатную сетку называют также километровой, а ее линии - километровыми.
Слайд 33Обозначение координатной сетки смежной зоны за рамки листа карты
Километровой сеткой
смежной зоны пользуются тогда, когда работа ведется с листами карт
на стыке двух зон и требуется пользоваться на всех этих листах единой системой координат. Эту сетку проводят карандашом на листах карт одной из этих зон, соединяя по линейке противоположные концы одноименных километровых (вертикальных и горизонтальных) линий сетки соседней зоны.
Слайд 35Определение по карте прямоугольных координат точки (А) и нанесение цели
(Ц) на карту по координатам (с помощью офицерской линейки)
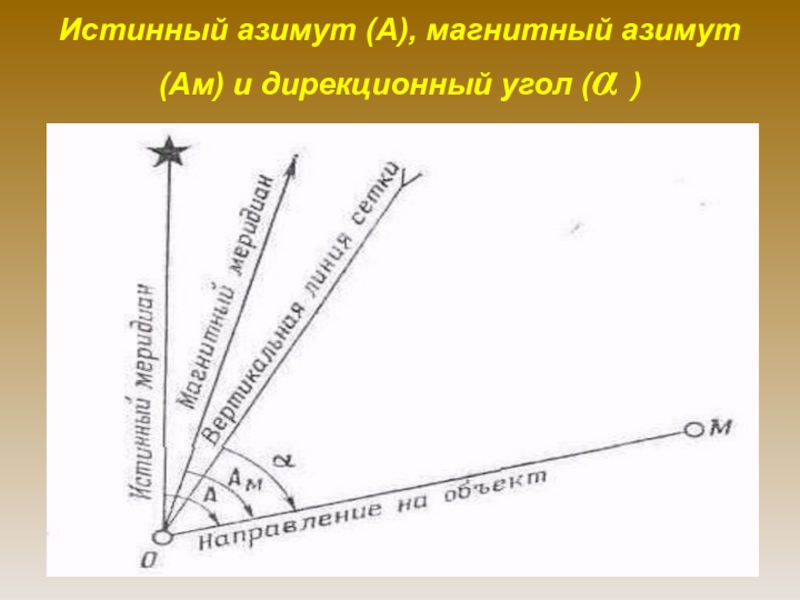
Слайд 37Дирекционный угол:
Дирекционным углом (α) какого-либо направления называется угол, измеряемый на
карте по ходу часовой стрелки от 0 до 360° между
северным направлением вертикальной километровой линии и направлением на определяемую точку. Использование в качестве начального направления вертикальной километровой линии позволяет просто и быстро строить и измерять дирекционные углы в любой точке карты.
Слайд 39Истинный азимут:
Истинным или географическим азимутом А направления называется угол, измеряемый
от северного направления географического меридиана по ходу часовой стрелки до
заданного направления. Как и дирекционный угол, истинный азимут может иметь любое значение от 0 до 360°.
Слайд 40Магнитный азимут:
Магнитным азимутом Ам направления называется горизонтальный угол, измеряемый по
ходу часовой стрелки (от 0 до 360°) от северного направления
магнитного меридиана до определяемого направления. Магнитные азимуты определяются на местности с помощью угломерных приборов, у которых имеется магнитная стрелка (у компасов и буссолей). Использование этого простого способа ориентирования направлений невозможно в районах магнитных аномалий и магнитных полюсов.
Слайд 41Магнитный меридиан:
При ориентировании на местности за направление меридиана обычно принимают
направление магнитной стрелки компаса. Оно не совпадает с направлением истинного
меридиана (так как северный географический полюс и северный магнитный полюс не совпадают) и лишь приближенно указывает направление север — юг. Направление магнитной стрелки называется - магнитным меридианом.
Слайд 42Магнитное склонение (δ - дельта):
Так как истинный и магнитный меридианы
не совпадают по направлениям, то между ними образуется угол, который
называется магнитным склонением (δ - дельта) .Склонение может быть восточным (магнитная стрелка отклоняется на восток от истинного меридиана) и западным (стрелка отклоняется на запад).
Слайд 44Сближение меридианов (γ - гамма) :
Между вертикальной линией координатной сетки
и истинным меридианом образуется угол, так как меридианы зоны сходятся
у полюсов в одной точке, в то время как вертикальные линии координатной сетки параллельны между собой. Этот угол называется сближением меридианов.
Слайд 45Определение поправки для перехода от дирекционного угла (а) к магнитному
азимуту (Ам) и обратно
Слайд 483.1 Простейшие способы приближенного определения расстояний:
1.Глазомер;
2.По измеренным угловым размерам предметов;
3.Измерение
расстояний шагами;
4.Определение расстояний по времени движения;
5.Определение расстояний по звуку
и вспышке выстрела;6.Определение расстояний на слух.
Слайд 49 1. Глазомер — основной, самый простой и быстрый способ, наиболее
доступный каждому сотруднику в любых условиях боевой обстановки. Глазомер вырабатывается
путем систематической тренировки, проводимой в разнообразных условиях местности, в различное время года и суток. Чтобы развить свой глазомер, необходимо возможно чаще, упражняться в оценке на глаз расстояний с обязательной проверкой их шагами, по карте или каким-либо другим способом.Начинать тренировку следует с коротких расстояний (10, 50, 100 м). С последующим переходом к большим (200, 400, 800, 1000 м), вплоть до предельных дальностей действительного огня стрелкового оружия.
Слайд 50 В процессе такой тренировки основное внимание надо обращать на учет
побочных явлений, которые влияют на точность глазомерного определения расстояний. Перечислим
основные из них:а) более крупные предметы кажутся ближе мелких, находящихся на том же расстоянии;
б) более близко расположенными кажутся предметы, видимые резче и отчетливее, поэтому:
— предметы яркой окраски (белой, желтой, красной) кажутся ближе, чем предметы темных цветов (черного, коричневого, синего);
Слайд 51— ярко освещенные предметы кажутся ближе слабо освещенных, находящихся на
том же расстоянии;
— во время тумана, дождя, в сумерки, в
пасмурные дни, при насыщенности воздуха пылью наблюдаемые предметы кажутся дальше, чем в ясные солнечные дни;— чем резче разница в окраске предметов и фона, на котором они видны, тем более уменьшенными кажутся расстояния до этих предметов; например, зимой снежное поле как бы приближает все находящиеся на нем более темные предметы.
Слайд 52в) чем меньше промежуточных предметов находится между глазом и наблюдаемым
предметом, тем этот предмет кажется ближе, в частности:
— предметы на
ровной местности кажутся ближе; особенно сокращенными кажутся расстояния, определяемые через обширные открытые водные пространства,— противоположный берег всегда кажется ближе, чем в действительности;— складки местности (овраги, лощины), пересекающие измеряемую линию, как бы уменьшают расстояние;
— при наблюдении лежа предметы кажутся ближе, чем при наблюдении стоя.
Слайд 53г) при наблюдении снизу вверх, от подошвы горы к вершине,
предметы кажутся ближе, а при наблюдении сверху вниз — дальше.
Слайд 54 Глазомерная оценка расстояний может облегчаться и контролироваться следующими приемами:
а) использованием
нескольких человек для измерения одной и той же линии независимо
друг от друга; среднее из всех определений будет наиболее точным результатом;б) сравнением измеряемого расстояния с другим, обозначенным на местности протяжением, величина которого известна (например, вблизи измеряемого участка может проходить воздушная линия связи или электросети, расстояние между столбами которой известно). Каждый может уточнить и дополнить эту табличку применительно к своим наблюдениям.
Слайд 55Точность глазомера зависит от натренированности наблюдателя, от величины определяемых расстояний
и от условий наблюдения.
Для дистанций до 1000м у достаточно
опытных наблюдателей ошибки обычно не превосходят 10—15% расстояния. При более значительных расстояниях они могут в отдельных случаях достигать 50%.
Слайд 572. Определение расстояний по измеренным угловым размерам предметов.
Применение этого
способа возможно, если известна наблюдаемая линейная величина (высота, ширина или
длина) предмета, до которого определяется расстояние Д. Способ сводится к измерению в тысячных угла, под которым виден этот Предмет, и к последующему решению задачи: по соотношению линейной (известной заранее) и угловой (измеренной) величин предмета определить расстояние до него.
Слайд 58На рис. показано, что дуга АК=Т, стягивающая угол, под которым
виден наблюдаемый предмет (дерево высотой В = АЕ), равна У
делениям угломера (на рисунке угол У взят равным 300 делениям угломера, т. е. 300 тысячным). Цена деления угломера равна одной тысячной доле дистанции, т. е. Д/1000. Следовательно, длина дуги Т будет: T = У×Д/1000
Слайд 59Для малых углов, не превышающих 300 тысячных (т. е. 18°),
можно с достаточной для практических целей точностью считать длину дуги
Т = АК и соответствующего ей отрезка В = АЕ равными между собой, т. е. Т = В. Подставляя это в формулу, получимВ:Д= У:1000
Слайд 60Для малых углов, не превышающих 300 тысячных (т. е. 18°),
можно с достаточной для практических целей точностью считать длину дуги
Т = АК и соответствующего ей отрезка В = АЕ равными между собой, т. е. Т = В. Подставляя это в формулу, получимВ:Д= У:1000
Эта пропорция носит название формулы тысячных.
Слайд 61Решая пропорцию относительно В или Д, получим соответственно:
а) формулу тысячных
для определения расстояний
Д = 1000×В/У
б) формулу тысячных для определения линейных
размеров предметовВ = Д×У/1000
Эти формулы дают достаточно точные результаты вычислений, если величина угла У не превышает 300 тысячных (3-00).
Слайд 62Определение расстояний по угловым размерам предметов дает точные результаты лишь
при условии, если хорошо известны действительные размеры наблюдаемых предметов и
угловые измерения производятся тщательно, с помощью измерительных приборов (бинокля, стереотрубы и т. п.). При измерениях же углов подручными предметами этот способ по точности не превосходит глазомерный способ.
Слайд 63Простейшие способы измерения углов.
Измерение углов полевым биноклем.
В поле зрения
бинокля имеются две взаимно-перпендикулярные угломерные шкалы для измерения горизонтальных и
вертикальных углов. Величина (цена) одного большого деления соответствует 0-10, а малого 0-05. Для измерения угла между двумя направлениями надо, глядя в бинокль, совместить какой-либо штрих угломерной шкалы с одним из этих направлений и подсчитать число делений до второго направления. Умножив затем этот отсчет на цену деления, получим величину измеряемого угла в тысячных.
Слайд 65Измерение углов с помощью линейки.
При отсутствии бинокля можно измерять углы
обычной линейкой с миллиметровыми делениями. Точность измерения углов этим способом
зависит от навыка в вынесении линейки точно на 50 см от глаза. В этом можно быстро натренироваться с помощью бечевки такой длины
Слайд 66 Если линейку держать перед собой на расстоянии 50 см от
глаза, то одно ее деление (1 мм) будет соответствовать
0-02.
В этом легко убедиться из самой сущности понятия тысячной: в данном случае Д = 50 см, т. е. одна тысячная этой дистанции равна 0,5 мм; поэтому одному миллиметру будет соответствовать угол, равный двум тысячным, т. е. 0-02.
Слайд 67 Измерение горизонтального и вертикального углов с помощью линейки. Угловое расстояние
между столбами 0-34; высота дерева 0-22.
Слайд 68
С помощью линейки удобно измерять малые углы и в градусах
(до 30°). В этом случае ее следует выносить на расстояние
60 см от глаза. Тогда 1 см на линейке будет соответствовать 1°.
Слайд 70 Вместо линейки с делениями можно использовать палец, ладонь или любой
подручный небольшой предмет (спичечную коробку, карандаш), размер которого в миллиметрах,
а следовательно, и в тысячных известен. Для измерения угла такая мерка также выносится на расстояние 50 см от глаза и по ней путем сравнения определяется искомая величина угла.
Слайд 713. Измерение расстояний шагами.
В боевой обстановке этот способ по
сравнению с другими имеет более ограниченное применение. В подразделениях он
используется, если позволяет обстановка, главным образом при составлении графических документов (схем ориентиров, схем обороны подразделений), а также для контрольных промеров, особенно выполняемых в учебных целях.
Слайд 72 Чтобы повысить точность измерения расстояний шагами, необходимо:
а) натренироваться в ходьбе
ровным шагом, особенно в неблагоприятных условиях (на подъемах и спусках,
при движении по кочковатому лугу, в кустарнике и т. п.);б) знать длину своего шага в метрах; она определяется из промера шагами линии, длина которой известна заранее и должна быть не менее 200—300 м.
Слайд 73 При измерении расстояний шаги считаются парами (обычно под левую ногу).
После каждой сотни пар шагов счет начинается снова. Чтобы не
сбиться, полезно каждую пройденную сотню пар отмечать на бумаге или же загибать последовательно пальцы руки.
Слайд 74 Принимая среднюю длину шага за 0,75 м, а пару шагов
за 1,6 м, можно приближенно считать, что расстояние в метрах
равно числу пар шагов, увеличенному в 1,5 раза. Для более точных подсчетов надо брать действительную длину своего шага.Ошибки определения расстояний шагами при ровном хорошо выверенном шаге в среднем достигают 2 — 4% измеренного расстояния.
Слайд 754. Определение расстояний по времени движения.
Этот способ полезно применять
в пути для приближенной контрольной оценки пройденного расстояния, например, при
передвижении на лыжах, ночью, в условиях плохой видимости и т. п. Для этого надо знать среднюю скорость своего движения. Например, средняя скорость движения походным шагом около 5 км/час, если подъемы и спуски на пути не превышают 5°.
Слайд 765. Определение расстояний по звуку и вспышке выстрела.
Этот способ
позволяет быстро определять расстояния до стреляющих орудий, минометов и других
целей, обнаруживающих себя в момент выстрела или взрыва вспышкой и образованием дымовых колец.
Слайд 77Для приближенного определения расстояний можно считать, что скорость распространения звука
в воздухе примерно равна, 330 м/сек, т. е. округленно 1
км в 3 сек. Свет же распространяется почти мгновенно. Таким образом, отсчитав по секундной стрелке часов время t в секундах от момента вспышки до момента слухового восприятия звука выстрела или взрыва, расстояние Д в километрах до цели получим по формулеД = t×Vзв.
Если, например, звук был услышан через 6 секунд после вспышки, то
Д = 6с×330 м/с = 1,9 км.
Слайд 78При отсутствии часов отсчитывать секунды можно путем порядкового счета про
себя двухзначных чисел, начиная с момента вспышки выстрела, например: двадцать
один, двадцать два и т. д. Отсчет каждого из этих чисел занимает примерно секунду. Навыки такого счета, соразмерного ходу секундной стрелки, довольно быстро приобретаются уже после двух — трех тренировок в отсчете секунд с проверкой быстроты счета по часам или секундомеру.
Слайд 79При более точных определениях расстояний время отсчитывается по секундомеру с
точностью до 0,1 секунды; отсчет t производится по трем —
четырем выстрелам и для вычисления расстояния берется среднее значение из всех приемов; берутся более точные данные о скорости распространения звука: летом — 340 м/сек, зимой — 320 м/сек и при температуре воздуха, близкой к 0°, — 330 м/сек. Например, если летом значение t при трех измерениях получилось равным 12,6 секунды, тоД = 12,6 x 340 = 4284 м.
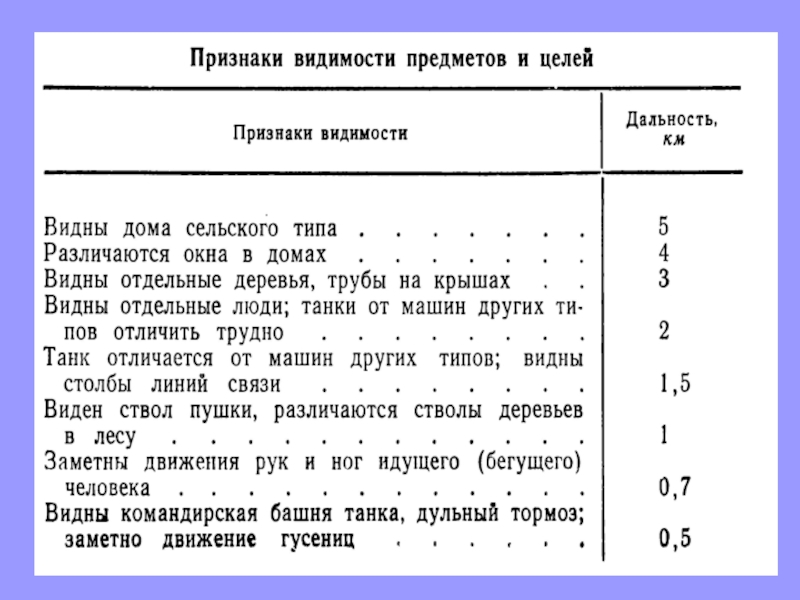
Слайд 806. Определение расстояний на слух. Ночью и в условиях плохой
видимости расстояния часто приходится оценивать на слух. Для этого надо
уметь определять по характеру звуков их источники и знать, с каких, примерно, расстояний можно услышать эти звуки. При нормальном слухе и благоприятных акустических условиях дальность слышимости примерно такая, какая показана в таблицах.
Слайд 82 Приведенные в таблицах данные приближенны и непостоянны. Они меняются в
зависимости от конкретных условий, в которых производятся наблюдения, поэтому должны
уточняться каждым наблюдателем на основе своего личного опыта. Точность определения расстояний этим способом зависит от опытности наблюдателя, остроты и натренированности его слуха и умения учитывать природные факторы, влияющие на распространение и силу звука.
Слайд 83 К основным из этих факторов относятся: направление и сила ветра,
температура и влажность воздуха, характер и расположение складок рельефа, растительность,
наличие экранирующих поверхностей, отражающих звук и вызывающих эхо и слуховые обманы. Наиболее сильно искажаются звуки по силе и направлению вблизи крупных водоемов и в закрытых местах — в лесу, в горах, в глубоких складках рельефа.
Слайд 84 Слышимость усиливается, когда ветер дует со стороны источника звука, а
также ночью и в ранние утренние часы, в пасмурную погоду,
особенно после дождя, у водной поверхности, в горах, зимой (при отсутствии снегопада) и в других случаях, когда улучшается звукопроводность воздуха. При усилении слышимости, вызываемом этими причинами, источники звука кажутся ближе, чем в действительности.
Слайд 85 Звук поглощается, т. е. становится слабее, в жаркую солнечную погоду,
во время снегопада, дождя, в лесу, кустарнике, на местности с
песчаным грунтом. При ослаблении слышимости расстояния до источников звука кажутся увеличенными.
Слайд 863.2 Определение крутизны скатов
1. Оценка на глаз.
Чтобы уметь
оценивать крутизну скатов на глаз, надо изучить на местности и
закрепить в зрительной памяти крутизну нескольких типичных скатов и затем путем мысленного сравнения с ними определять крутизну других скатов.
Слайд 87Более точные результаты получаются, если, зайдя сбоку ската, сравнить на
глаз его крутизну с величиной какого-либо имеющегося под рукой эталона
угла. Так, например, можно использовать обычный чертежный целлулоидный треугольник, величины углов которого известны (рис.).
Слайд 88Измерив заранее углы между расставленными до предела большим, указательным и
средним пальцами руки, можно пользоваться и этими углами для оценки
на глаз крутизны скатов.
Слайд 892. Сравнение высоты ската с его заложением.
В таблице приближенно
указано, во сколько раз при данной крутизне высота ската меньше
его заложения.Запоминать эти цифры не требуется, так как все они легко получаются от деления постоянного числа 60 на число градусов крутизны.
Слайд 90Для определения крутизны по этому способу надо:
а) зайти сбоку
ската, держа перед собой на уровне глаз карандаш и записную
книжку, как показано на рис.;
Слайд 91б) оценить на глаз или с помощью делений, которые могут
быть для этой цели нанесены на записной книжке, во сколько
раз выдвинутая часть карандаша ЕС, т. е. высота скаута, короче горизонтального обреза книжки АС, т. е. заложения ската;в) разделить 60° на полученное число; частное от деления покажет крутизну ската в градусах.
Пример. На рис. высота ската ЕС меньше его заложения АС в 3 раза. Следовательно, крутизна ската α будет α ˚ = 60˚/3 = 20˚
Слайд 923. Промер шагами.
Крутизна ската этим способом определяется по приближенной
формуле α ˚ = 60˚/ПШ,
где ПШ — протяженность ската, измеренная
парами шагов.Для определения по этой формуле крутизны ската становятся в точке А и, держа на уровне глаз горизонтально папку или книжку, визируют вдоль нее.
Слайд 93На продолжении линии визирования замечают на скате какую-либо точку С.
Затем, двигаясь по направлению к этой точке, измеряют парами шагов
расстояние Д до нее от точки А.Пример (рис.). От начала подъема (точка А) до точки С на скате отсчитано 4 пары шагов. Крутизна ската
α ˚ = 60˚/4 = 15°.
Слайд 944. Определение крутизны ската эклиметром.
Эклиметром называется угломерный прибор для
измерения наклона линий местности к горизонту. Простейший эклиметр нетрудно изготовить
самому.
Слайд 95На обложке записной книжки, куске картона или фанеры (рис.) параллельно
обрезу проводится прямая линия АВ.
Слайд 96Из середины С этой линии описывается полуокружность и проводится перпендикуляр
к линии АВ, Точка пересечения перпендикуляра с полуокружностью обозначается 0
(нуль градусов). В обе стороны от нее наносятся с помощью транспортира деления через каждые 2° или 5°.
Слайд 97Деления подписываются, как показано на рисунке. Остается к центру С
подвесить на нитке груз М, и эклиметр готов к работе.
Слайд 98Чтобы определить крутизну ската, эклиметр держат на уровне глаз так,
чтобы линия визирования АВ (рис.) была параллельна направлению ската. Для
этого следует визировать в точку N, расположенную над скатом на той же высоте, что и глаз наблюдателя. При таком положении эклиметра нить его отвеса уклонится от 0° на угол а и покажет отсчет, равный углу крутизны ската.
