Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Виртуальная память
Содержание
- 1. Виртуальная память
- 2. 4. Организация хранения и доступа (физический уровень)4.1.
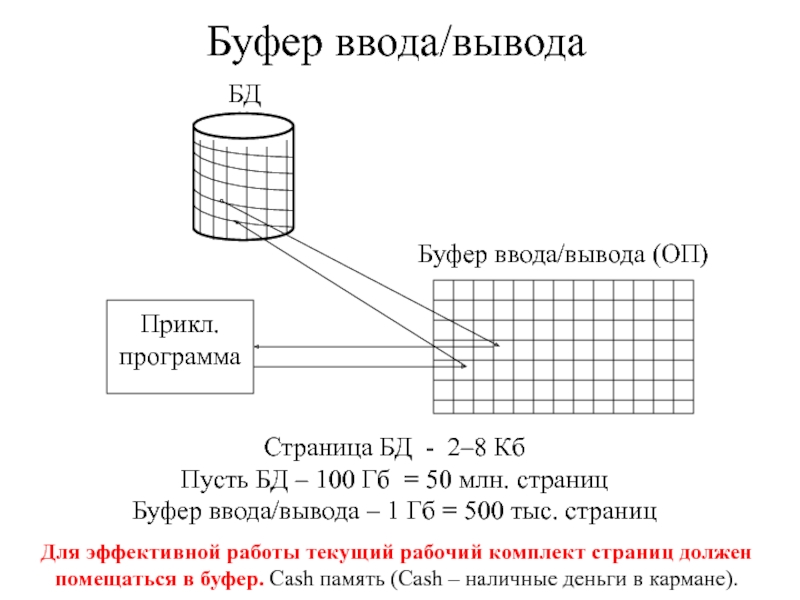
- 3. Буфер ввода/выводаБДПрикл.программаБуфер ввода/вывода (ОП)Страница БД - 2–8
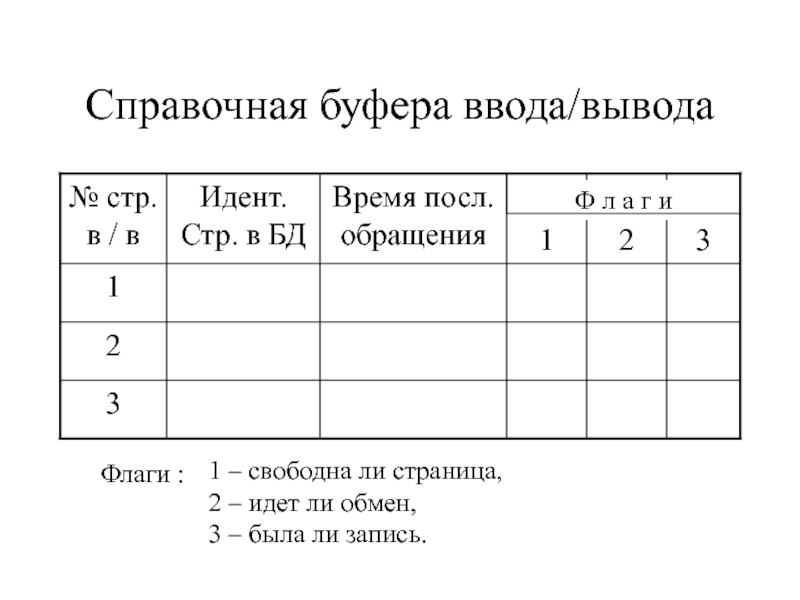
- 4. Справочная буфера ввода/выводаФ л а г иФлаги
- 5. 4.2. Массивы и списки 4.2.1. Однородные массивы
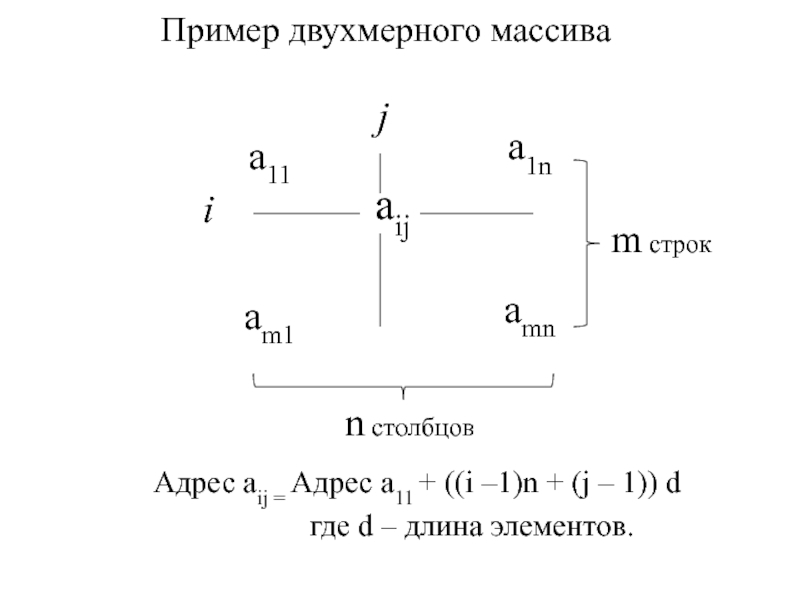
- 6. aij a11a1namnam1Пример двухмерного массиваm строкn столбцовijАдрес
- 7. 4.2.2. Неоднородные массивы Массив называется неоднородным,
- 8. 4.2.2. dbf - форматЕсли нужно описать таблицу
- 9. 4.2.3. Языки разметкиСтандарт ISO c 1996 г.
- 10. 4.3. Стеки, очереди, декиСтек – список с
- 11. 4.4. Корневые деревьяДерево – это граф, у
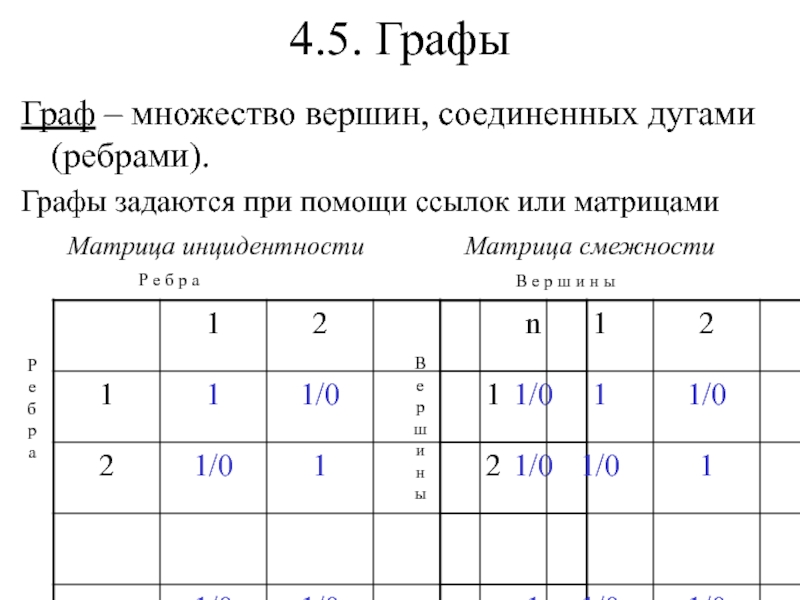
- 12. 4.5. ГрафыГраф – множество вершин, соединенных дугами
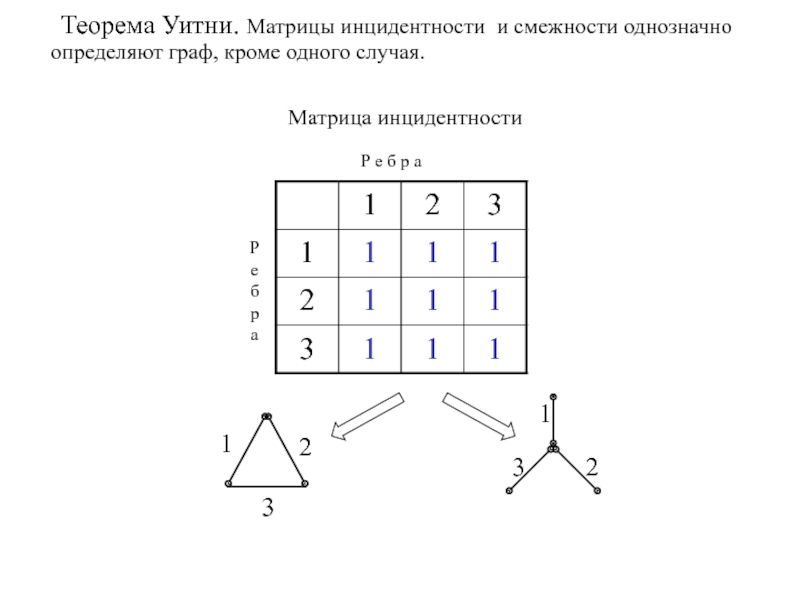
- 13. Р е б р а РебраМатрица инцидентности
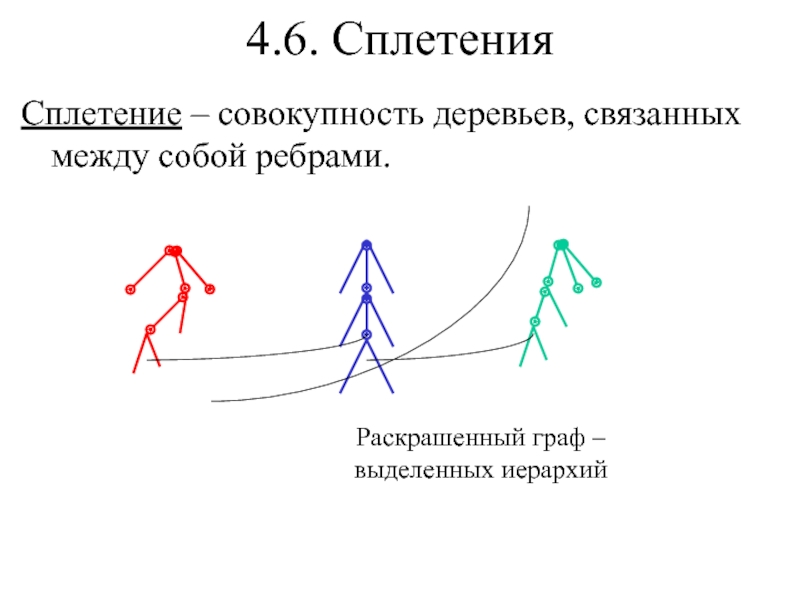
- 14. 4.6. СплетенияСплетение – совокупность деревьев, связанных между собой ребрами.
- 15. 4.6. СплетенияСплетение – совокупность деревьев, связанных между собой ребрами.Раскрашенный граф –выделенных иерархий
- 16. 5. Индексирование. Поиск по ключуИндекс – единственный
- 17. 5.1. Плотный индексИспользуется для неоднородных и несортированных
- 18. 5.1. Плотный индексИспользуется для неоднородных и несортированных
- 19. 5.2. Разреженный индексИспользуется для сортированных массивов.Массив: Ид
- 20. Область переполненияЕсли при наполнении массива новое данное
- 21. Область переполненияИ на странице i заводится ссылка
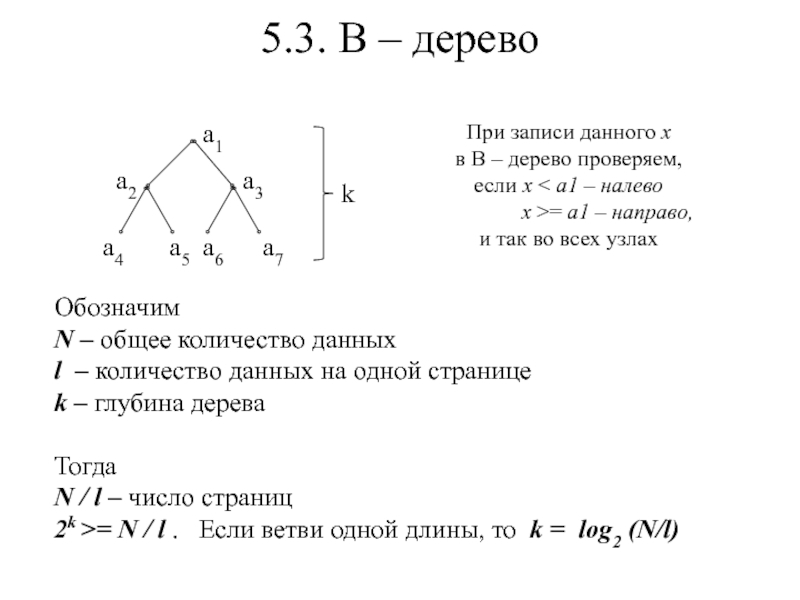
- 22. 5.3. В – дерево a1a3a2a4a5a6a7kПри записи данного
- 23. Сбалансированные деревья kОпределение. В – дерево называется
- 24. 5.4. ХешированиеХеш – функция F (ключ) =
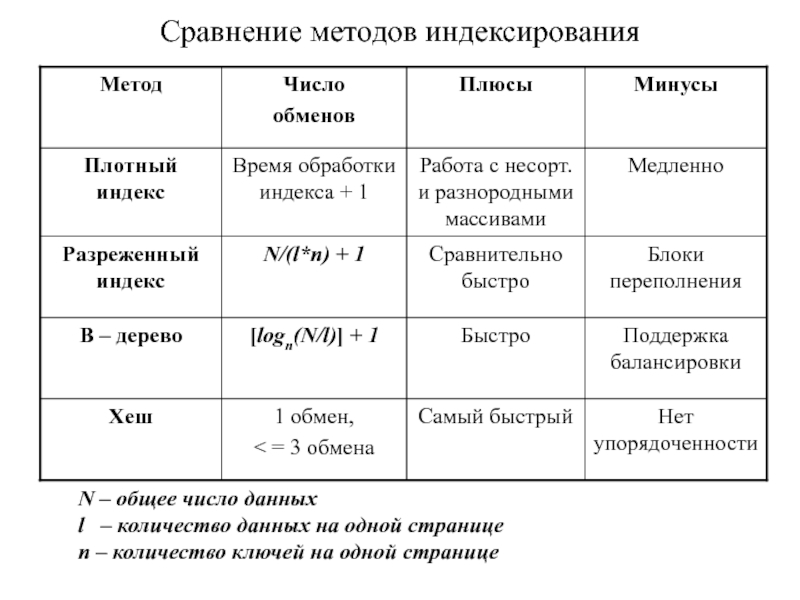
- 25. Сравнение методов индексированияN – общее число данныхl
- 26. Скачать презентанцию
4. Организация хранения и доступа (физический уровень)4.1. Виртуальная памятьОсуществляет вызов страниц с магнитных носителей в оперативную память. Реализует механизм виртуальной памяти.
Слайды и текст этой презентации
Слайд 24. Организация хранения и доступа (физический уровень)
4.1. Виртуальная память
Осуществляет вызов
Слайд 3Буфер ввода/вывода
БД
Прикл.
программа
Буфер ввода/вывода (ОП)
Страница БД - 2–8 Кб
Пусть БД –
100 Гб = 50 млн. страниц
Буфер ввода/вывода – 1 Гб
= 500 тыс. страницДля эффективной работы текущий рабочий комплект страниц должен помещаться в буфер. Cash память (Cash – наличные деньги в кармане).
Слайд 4Справочная буфера ввода/вывода
Ф л а г и
Флаги :
1 – свободна
ли страница,
2 – идет ли обмен,
3 – была ли запись.
Слайд 54.2. Массивы и списки
4.2.1. Однородные массивы
Массив называется
однородным, если длина и формат всех элементов одинаковы
Такие массивы замечательны
тем, что легко определяется адрес любого элемента
Слайд 6 aij
a11
a1n
amn
am1
Пример двухмерного массива
m строк
n столбцов
i
j
Адрес aij = Адрес
a11 + ((i –1)n + (j – 1)) d
где d – длина элементов.
Слайд 74.2.2. Неоднородные массивы
Массив называется неоднородным, если длина и
формат элементов могут быть разными.
Пусть элементы a1,…,an имеют описатели a1,…,an
Тогда
данные можно представить (a1 a1 ,…, an an)Или (n a1…an a1…an ), если все описатели ai одинаковой длины и содержат длину данного ai
Слайд 84.2.2. dbf - формат
Если нужно описать таблицу из m строк
с
n атрибутами a1,…,an в каждой строке, то в
dbf
-формате это будет будет представлено так n m a1…an (a1…an )1 … ( a1…an )m
n m
Такой формат применил Рэтлифф в СУБД dBASE, которая быстро получила распространение, а
dbf-формат стал всемирным стандартом на ~ 20 лет.
Слайд 94.2.3. Языки разметки
Стандарт ISO c 1996 г.
- SGML
(Standard Generalized Markup Language)
- XML (Extensible Markup Language)
- HTML (Hypertext Markup Language) SGML XML HTML
HTML - стандарт для описания страниц в интернет
В XML есть секция DTD (Document Type Definition), которая описывает структуру данных – аналог схемы БД
В HTML заданный набор объектов, в XML можно создавать свои объекты
Общий стиль описания:
<имя объекта1>
<имя подоб1.1>
<имя данного 1> данное 1 < /имя данного 1>
<имя данного 2> данное 2 < /имя данного 2>
……
< /имя подоб1.1>
……
< /имя объекта1>
Слайд 104.3. Стеки, очереди, деки
Стек – список с включением и исключением
на одном конце. Метод LIFO (Last In First Out)
Очередь
– список, включение на одном конце, а исключение на другом. Метод FIFO (First In First Out) Дек – включение и исключение на обоих концах, сокращение от Double Ended Que.
Слайд 114.4. Корневые деревья
Дерево – это граф, у которого есть выделенная
вершина – корень. Если его убрать, все остальные вершины распадаются
на m > 0 поддеревьев
Слайд 124.5. Графы
Граф – множество вершин, соединенных дугами (ребрами).
Графы задаются при
помощи ссылок или матрицами
Матрица инцидентности
Матрица смежностиР е б р а
Р
е
б
р
а
В е р ш и н ы
В
е
р
ш
и
н
ы
Слайд 13Р е б р а
Р
е
б
р
а
Матрица инцидентности
Теорема
Уитни. Матрицы инцидентности и смежности однозначно
определяют граф, кроме одного случая.1
2
3
3
2
1
Слайд 154.6. Сплетения
Сплетение – совокупность деревьев, связанных между собой ребрами.
Раскрашенный граф
–
выделенных иерархий
Слайд 165. Индексирование. Поиск по ключу
Индекс – единственный способ быстрого доступа.
Построение
индекса – предварительная обработка информации или online поддержка при вводе
данных.
Слайд 175.1. Плотный индекс
Используется для неоднородных и несортированных массивов.
Массив: Идентификатор 1,
данное 1; Ид 2, дан 2; Ид 3, дан 3;
…. Ид n, дан n.Плотный индекс: Ид 1, адрес 1; Ид 2, адр 2; Ид 3, адр 3; …. Ид n, адр n.
Слайд 185.1. Плотный индекс
Используется для неоднородных и несортированных массивов.
Массив: Идентификатор 1,
данное 1; Ид 2, дан 2; Ид 3, дан 3;
…. Ид n, дан n.Плотный индекс: Ид 1, адрес 1; Ид 2, адр 2; Ид 3, адр 3; …. Ид n, адр n.
Плотный индекс – однородный массив, который можно отсортировать и потом искать делением пополам.
Слайд 195.2. Разреженный индекс
Используется для сортированных массивов.
Массив:
Ид 11, дан 11;
Ид 21, дан 21; …. Ид n1, дан n1
Страница
1……..
Ид 1N, дан 1N; Ид 2N, дан 2N; …. Ид nN, дан nN
Страница N
Индекс:
Ид 11, адрес стр 1; Ид 12, адрес стр 2; …. Ид 1N, адрес стр N
В индекс помещаются Идентификаторы первых данных всех страниц.
Слайд 20Область переполнения
Если при наполнении массива новое данное Ид ki, дан
ki не помещается на страницу i, то заводится новая страница
и часть страницы переносится в новую (область переполнения).Ид 1i, дан 1i; …. Ид ki, дан ki; …. Ид ni, дан ni
Страница i
Ид 1i, дан 1i; …. Ид ki, дан ki;
Страница i
Ид (k+1)i, дан (k+1)i; …. Ид ni, дан ni
Страница N+m (область переполнения страницы i)
Слайд 21Область переполнения
И на странице i заводится ссылка на область ее
переполнения.
Ид 1i, дан 1i; …. Ид ki, дан ki; Адрес
Страницы N+m Страница i
Ид (k+1)i, дан (k+1)i; …. Ид ni, дан ni
Страница N+m (область переполнения страницы i)
Слайд 225.3. В – дерево
a1
a3
a2
a4
a5
a6
a7
k
При записи данного x
в
В – дерево проверяем,
если x < a1 – налево
x >= a1 – направо,и так во всех узлах
Обозначим
N – общее количество данных
l – количество данных на одной странице
k – глубина дерева
Тогда
N / l – число страниц
2k >= N / l . Если ветви одной длины, то k = log2 (N/l)
Слайд 23Сбалансированные деревья
k
Определение. В – дерево называется сбалансированным по
вертикали, если длины всех его ветвей отличаются не более чем
на 1.Тогда k = [log2 (N/l)] + 1. Это число необходимых сравнений, в больших массивах оно обычно равно числу обменов с внешней памятью.
Определение. Дерево называется сбалансированным по горизонтали, если все веера подчиненных вершин отличаются не более чем на 1, | n - n1 | <= 1.
n
n1
Если n-арное дерево сбалансировано по вертикали и горизонтали, то
k = [logn (N/l)] + 1
Поэтому вместо бинарных деревьев обычно используются n-арные деревья.
n - максимальное число ссылок на странице.
Слайд 245.4. Хеширование
Хеш – функция
F (ключ) = идентификатор
Если из длинного
ключа сделать короткий идентификатор, то возможна коллизия: F (ключ1)
= F (ключ2)На странице, определяемой идентификатором, записываются
Ключ 1, дан 1; Ключ 2, дан 2; …. Ключ n, дан n и м. б. ссылка на страницу переполнения
Слайд 25Сравнение методов индексирования
N – общее число данных
l – количество
данных на одной странице
n – количество ключей на одной странице
