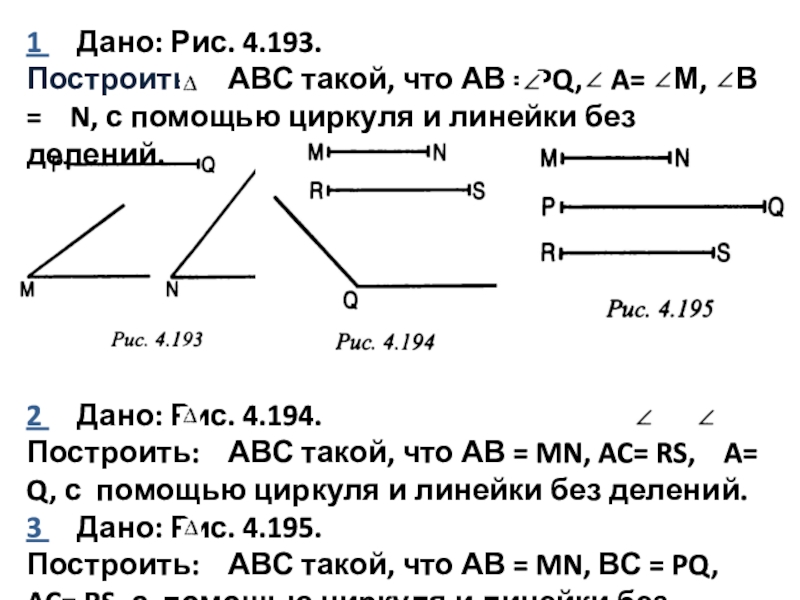
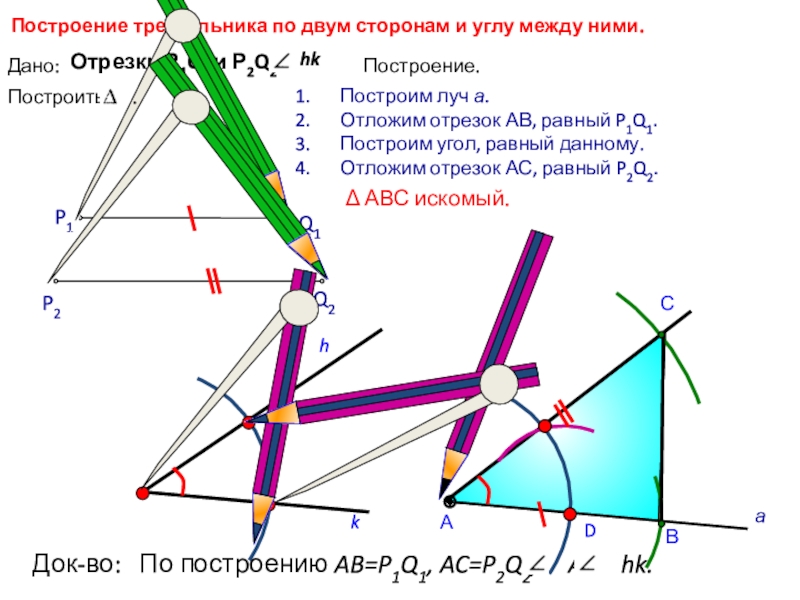
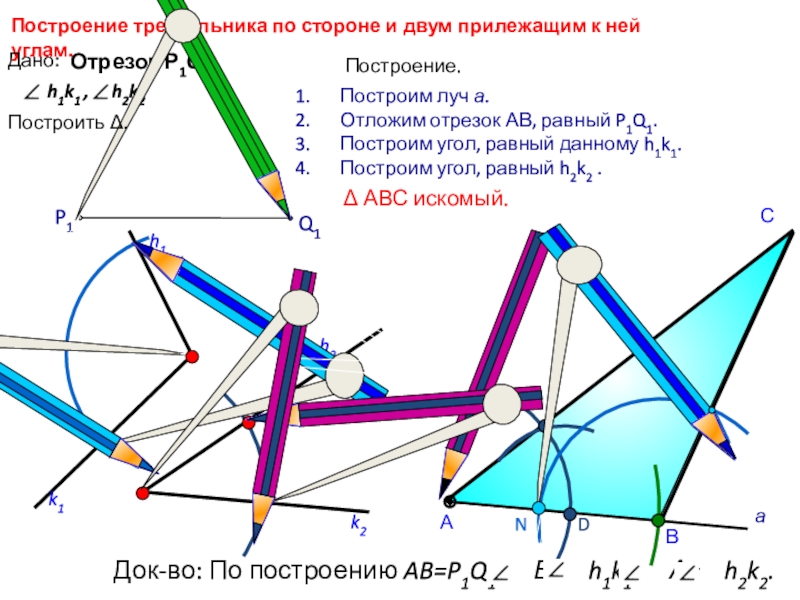
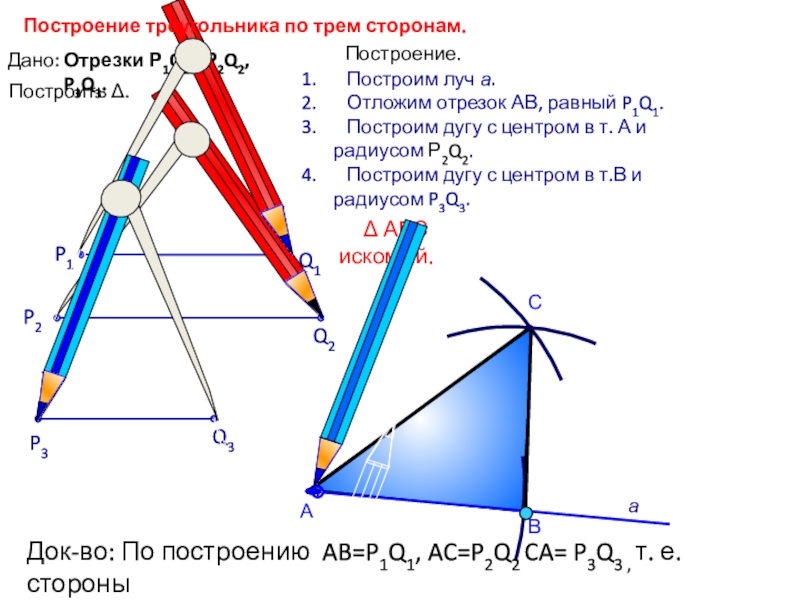
называется расстоянием от точки до прямой?
5. Что называется расстоянием между
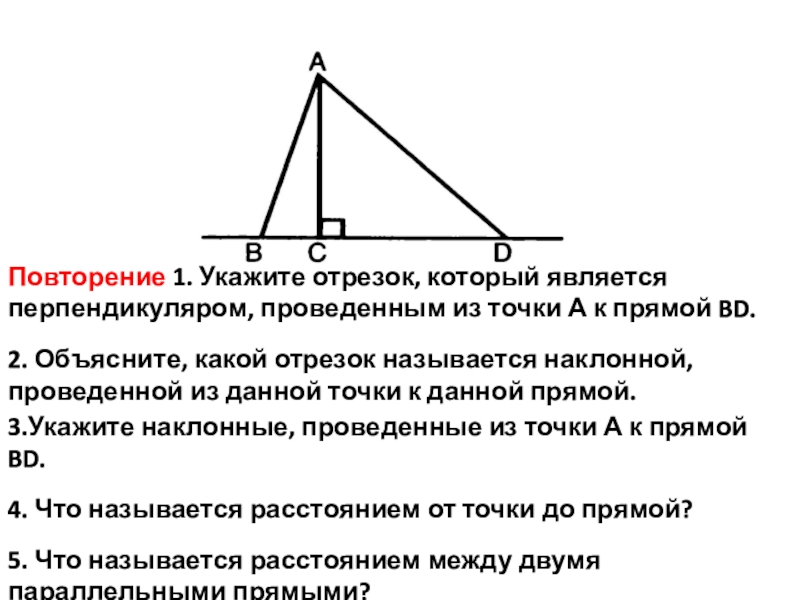
двумя параллельными прямыми?Повторение 1. Укажите отрезок, который является перпендикуляром, проведенным из точки А к прямой BD.
2. Объясните, какой отрезок называется наклонной, проведенной из данной точки к данной прямой.