Слайд 1
«ЭКОНОМЕТРИКА»
Илона Юловна Парик
К.э.н. Доцент
Кафедра статистики и эконометрики
Слайд 2
Основная литература
Эконометрика: учебник для магистрантов / И.И. Елисеева [и др.];
под ред. И.И.Елисеевой. ‑ М.: Издательство Юрайт, 2014
Эконометрика: учебник для
бакалавриата и магистратуры/ И.И. Елисеева [и др.]; под ред. И.И.Елисеевой. ‑ М.: Издательство Юрайт, 2018
Курышева С.В. Анализ временных рядов и прогнозирование: учебное пособие / С.В.Курышева, М.В. Боченина. – СПб. : Изд-во СПбГЭУ, 2014
Практикум по эконометрике: учеб. пособие / И.И.Елисеева, С.В.Курышева, Н.М.Гордеенко и др.; под ред. И.И.Елисеевой. ‑ 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2008
Слайд 3
Дополнительная литература
Айвазян С.А. Методы эконометрики. ‑ М.: Инфра-М, 2010
Афанасьев В.Н.,
Юзбашев М. М. Анализ временных рядов и прогнозирование. – М.:
Финансы и статистика, 2010
Доугерти К. Введение в эконометрику: Учебник. 2-е изд. / Пер. с англ. – М.: ИНФРА – М, 2007
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный дисциплина: учебник. – М.: Дело, 2009
Практикум по эконометрике: учеб. пособие / И.И.Елисеева, С.В.Курышева, Н.М.Гордеенко и др.; под ред. И.И.Елисеевой. ‑ 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2008
Чураков Е. П. Прогнозирование эконометрических временных рядов: учебник. ‑ М.: Финансы и статистика, 2008
Слайд 4
Рагнар Антон Киттиль Фриш
(норв. Ragnar Anton Kittil Frisch)
(1895-1973)
Слайд 51926 г. норвежский экономист Рагнар Фриш (1895-1973) предложил использовать термин
«эконометрика» для обозначения самостоятельной отрасли научных исследований
Развернутое определение эконометрики было
дано Рагнаром Фришем во вступительной статье первого номера журнала "Эконометрика" в 1933 г.
Слайд 6
Эконометрика – это наука, которая дает конкретное количественное выражение общим
(качественным) взаимосвязям экономических явлений и процессов, обусловленным экономической теорией
Слайд 7
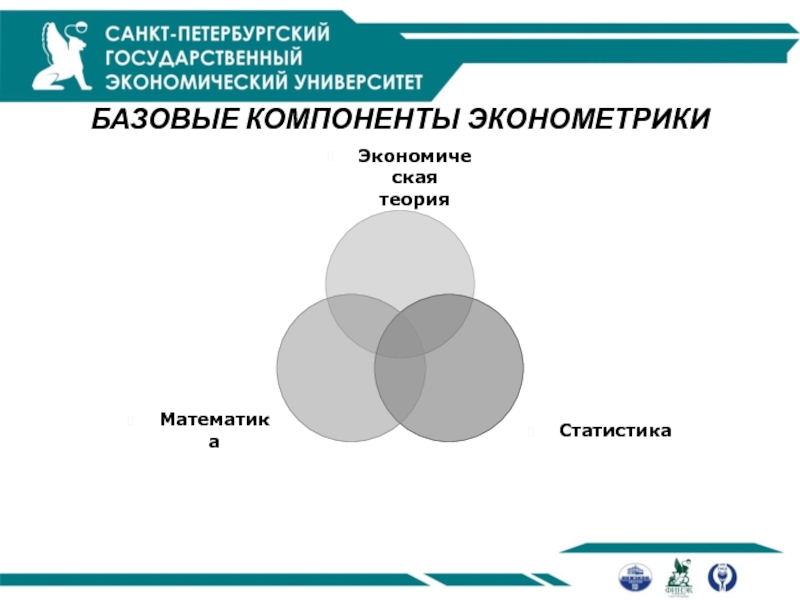
БАЗОВЫЕ КОМПОНЕНТЫ ЭКОНОМЕТРИКИ
Слайд 8На основе экономической теории разрабатываются концепции развития изучаемых процессов
С помощью
статистики эти процессы выражаются в статистических показателях
Математико-статистические методы позволяют строить
модели изучаемых процессов, оценивать их параметры, степень соответствия реальным данным и прогнозировать развитие изучаемого явления
Слайд 9
Главный инструмент эконометрики – эконометрическая модель, параметры которой оцениваются с
помощью методов математической статистики
Слайд 10
Этапы построения эконометрической модели
Теоретическое описание рассматриваемого экономического процесса с отражением
существующих тенденций
Сбор данных, анализ их качества
Спецификация модели. Устанавливаются экзогенные (внешние)
и эндогенные (внутренние) переменные, выявляются связи и соотношения, определяется вид модели исходя из соответствующей теории связи между переменными
Оценка параметров модели
Верификация модели, то есть проверка достоверности построенной модели
Интерпретация результатов
Слайд 11
ПРИМЕНЕНИЕ ПАРНОЙ РЕГРЕССИИ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНЯХ
Выбор типа математической функции при
построении уравнения регрессии
Оценка параметров уравнения парной линейной регрессии
Показатели силы связи
в моделях парной регрессии
Показатели тесноты связи в моделях парной регрессии
Статистическая оценка достоверности регрессионной модели
Интервальная оценка параметров уравнения парной регрессии
Использование модели парной регрессии для прогнозирования
Слайд 12
Задачи корреляционно-регрессионного анализа
Измерение параметров уравнения, выражающего связь между признаками. Эта
задача решается оценкой параметров уравнения регрессии
Измерение тесноты связи между признаками.
Данная задача решается показателей корреляции
Слайд 13
Виды функций, наиболее часто используемые в эконометрическом моделировании
Слайд 14
Методы выбора типа математической функции
Аналитический метод (теоретический анализ связи рассматриваемого
фактора и результата)
Графический метод
Экспериментальный метод
Слайд 15
Линеаризация нелинейных уравнений
Слайд 16
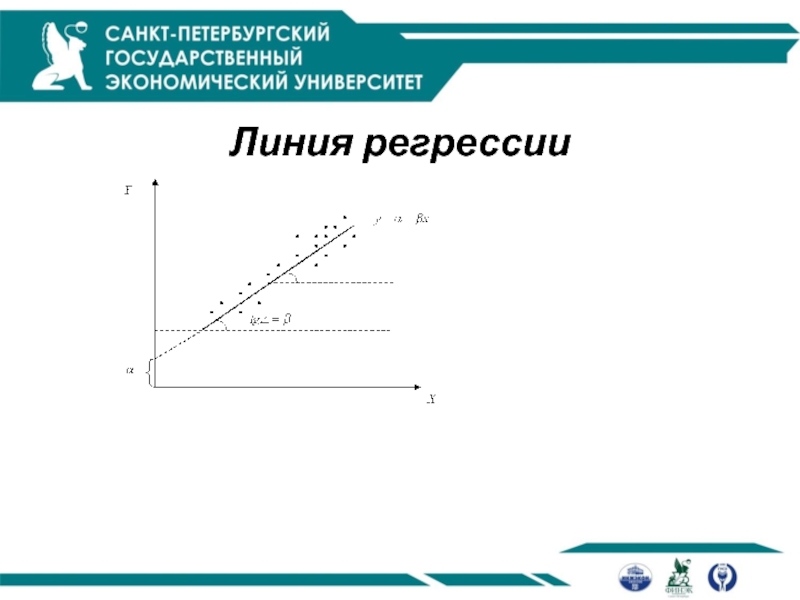
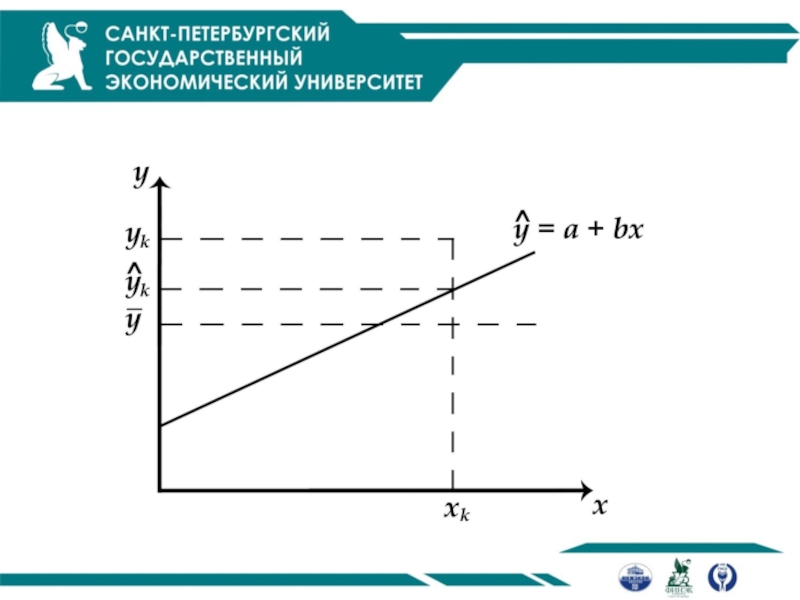
Оценка параметров уравнения парной линейной регрессии
Для оценки параметров функций, линейных
по параметрам, используется метод наименьших квадратов (МНК)
МНК позволяет получить такие
оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака от теоретических минимальна:
Слайд 17
Оценка параметров уравнения парной линейной регрессии
Для линейных и нелинейных уравнений,
приводимых к линейным, решается следующая система относительно и
:
Слайд 18
Формулы расчета параметров уравнения парной регрессии
- свободный член уравнения регрессии (пересечение, intercept). Экономически не интерпретируется.
- наклон линии регрессии (slope) или коэффициент регрессии. Он является мерой зависимости переменной от переменной .
В линейном уравнении регрессии параметр является абсолютным показателем силы связи
Слайд 20
Условия применения МНК
Модель регрессии должна быть линейной по параметрам
Число наблюдений
должно быть больше числа оцениваемых параметров (в 5-6 раз)
Значения переменной
x не должны быть одинаковыми
Изучаемая совокупность должна быть однородной
Модель регрессии должна быть корректно специфицирована
Значения ошибки (остатка)- случайные. Их изменение не образует
определенной модели
Отсутствие взаимосвязи между фактором x и остатком
В модели не должно наблюдаться тесной взаимосвязи между факторами (условие для множественной регрессии)
Слайд 26
Показатели силы связи в моделях парной регрессии
Абсолютные. Показывают, на сколько
единиц в среднем изменяется результативный признак при изменении факторного признака
на одну единицу. В линейном уравнении параметр - абсолютный показатель силы связи
Относительные (коэффициенты эластичности). Показывают, на сколько процентов в среднем изменяется результативный признак при изменении факторного признака на один процент
Слайд 27
Абсолютные и относительные показатели силы связи для основных видов функций
Слайд 29
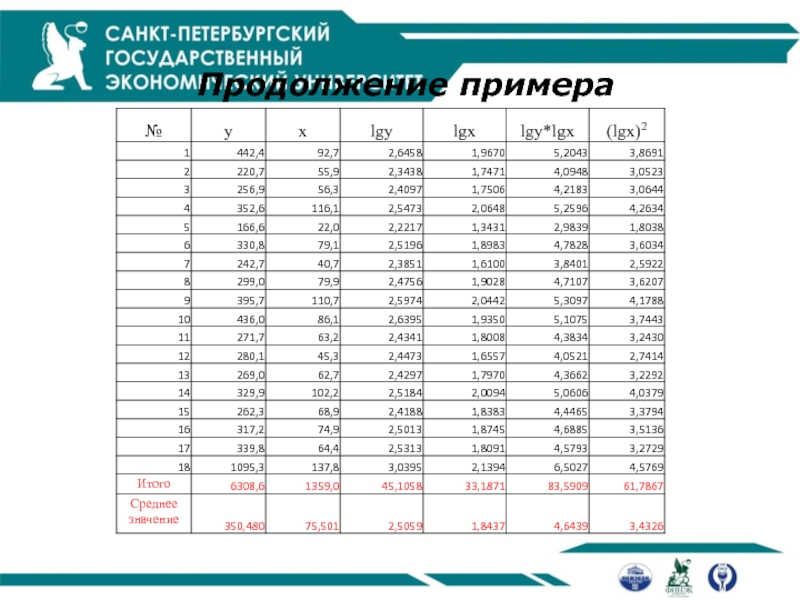
Продолжение примера
Степенная функция:
Слайд 30
Показатели тесноты связи в моделях парной регрессии
Коэффициент детерминации
показывает долю вариации
(дисперсии) результативного признака, объясняемую регрессией, в общей вариации результата
Слайд 32
Правило сложения дисперсий
- общая сумма квадратов отклонений (total sum of squares)
- факторная сумма квадратов отклонений (sum of squares due to regression)
- остаточная сумма квадратов отклонений (sum of squares due to error)
Слайд 35
Шкала значений коэффициента (индекса) корреляции
До 0,3 связь слабая
0,3-0,5 связь
умеренная
0,5-0,7 связь заметная
0,7-0,9 связь высокая
0,9-1,0 связь весьма высокая, близкая к
функциональной
Слайд 36
Свойства линейного коэффициента корреляции
Это стандартизованный коэффициент регрессии
Сравним для признаков, имеющих
различные единицы измерения
Если связь между y и x отсутствует, то
;
если , это не всегда означает отсутствия связи (связь может быть нелинейной)
Слайд 37
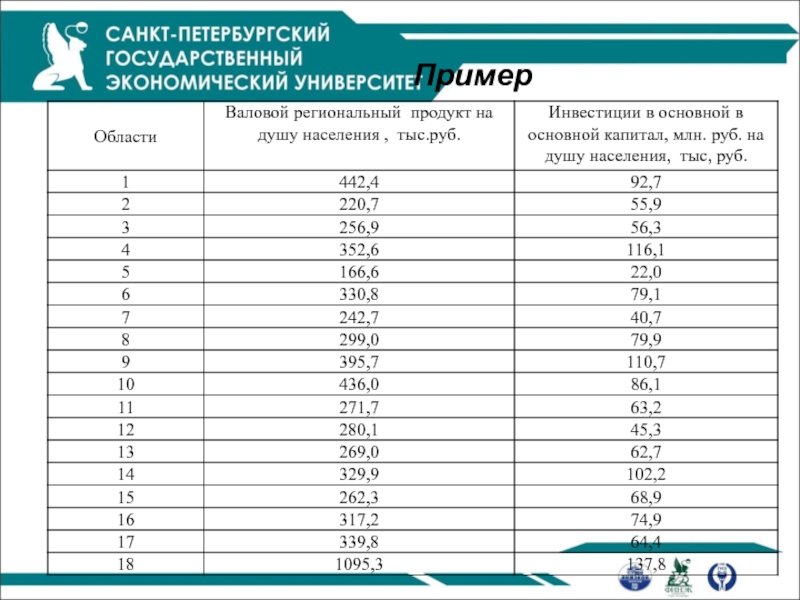
Продолжение примера
Линейная функция
Слайд 38
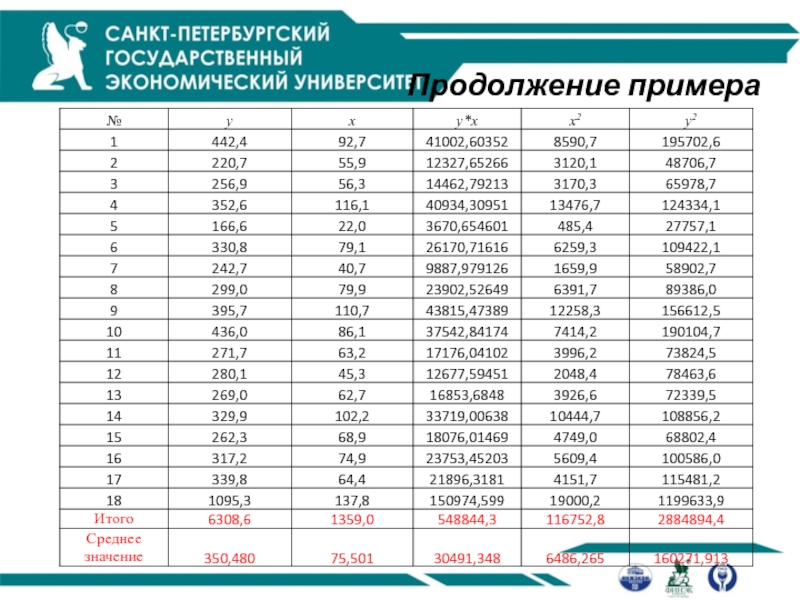
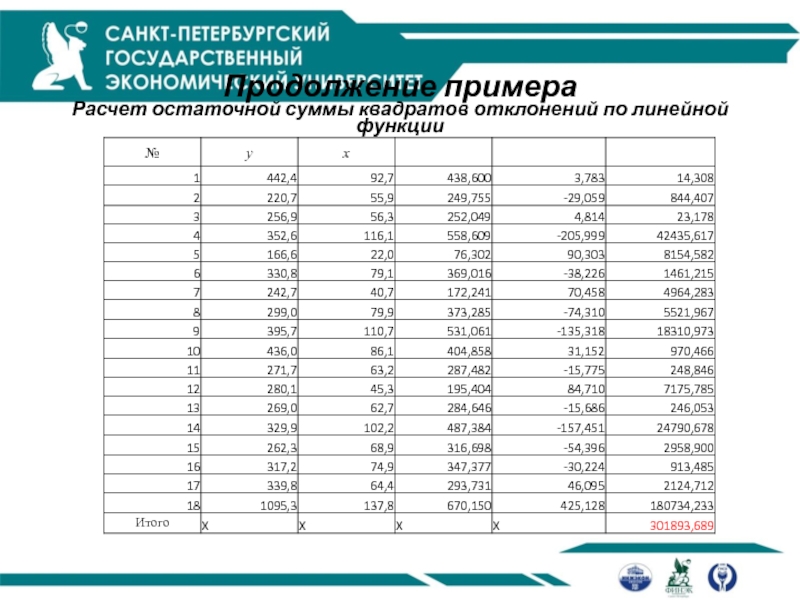
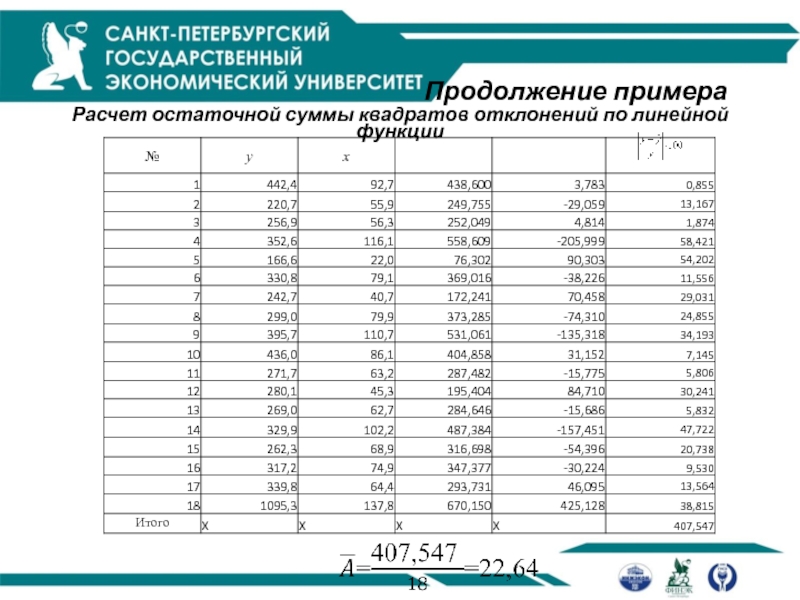
Продолжение примера
Расчет остаточной суммы квадратов отклонений по линейной функции
Слайд 39
Продолжение примера
Расчет теоретических значений результативного признака линейной функции
Слайд 40
Продолжение примера
Расчет коэффициента детерминации для линейной функции
Слайд 41
Продолжение примера
Расчет показателей корреляции
Слайд 42
Статистическая проверка гипотез
Статистической гипотезой называется предположение о свойстве генеральной
совокупности, которое можно проверить, опираясь на данные выборки. Обозначается буквой
H (лат. hypothesis)
Слайд 43
Статистическая оценка достоверности регрессионной модели
Выдвигается H0 :r2 в генеральной совокупности
Выдвигается H1: r2 в генеральной совокупности
Определяется уровень значимости (1 минус доверительная вероятность)
Рассчитывается критерий Фишера
Определяется табличное значение критерия Фишера
Фактическое значение сравнивается с табличным
Слайд 44
Оценка значимости уравнения регрессии
Если F>Ftab. , то гипотеза о случайной
природе оцениваемых характеристик отклоняется и признается статистическая значимость и надежность
уравнения
Если F
Слайд 45Критическая область – это область, попадание значения статистического критерия в
которую приводит к отклонению H0 . Вероятность попадания значения критерия
в эту область равна приятому уровню значимости (1 минус доверительная вероятность)
Область допустимых значений - область, попадание значения статистического критерия в которую приводит к принятию нулевой гипотезы
Слайд 46
Число степеней свободы (degrees of freedom - df) - число
свободно варьируемых переменных
n - число единиц совокупности
m - число
параметров при переменных(число факторов)
Слайд 48
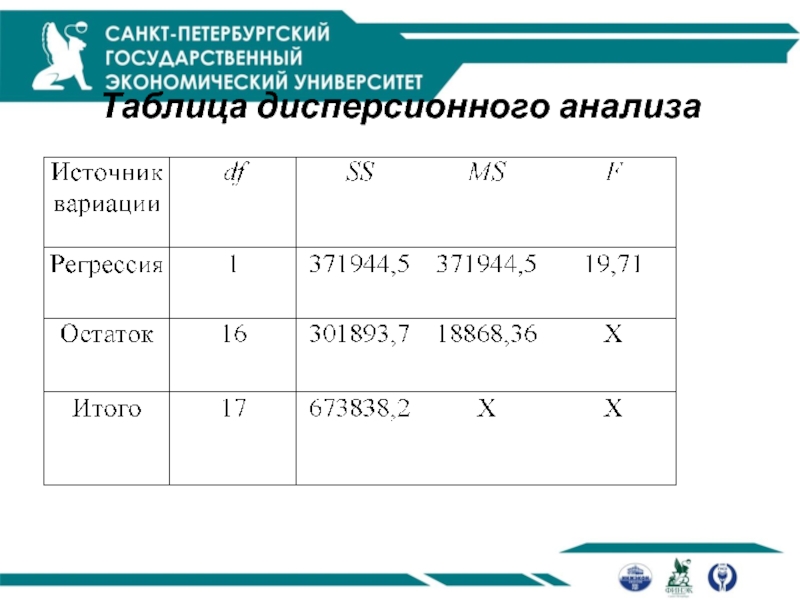
Продолжение примера
Расчет критерия Фишера
Слайд 50
Оценка качества модели на основе ошибки аппроксимации
Продолжение примера
Расчет
остаточной суммы квадратов отклонений по линейной функции
Слайд 52
Оценка значимости коэффициентов регрессии
Выдвигается : коэффициент регрессии
в генеральной совокупности равен 0
Выдвигается
: коэффициент регрессии в генеральной совокупности не равен 0
Определяется уровень значимости
Рассчитывается критерий Стьюдента
Определяется табличное (критическое) значение критерия Стьюдента ttab.
Фактическое значение сравнивается с табличным
Слайд 53Если t>ttab., то отклоняется, то есть параметр
не случайно отличается от нуля, и сформировался
под влиянием систематически действующего фактора
Если t
Слайд 54
Расчет критерия Стьюдента
- случайная ошибка коэффициента
регрессии
Слайд 57
Построение доверительных интервалов для коэффициентов регрессии
Слайд 58
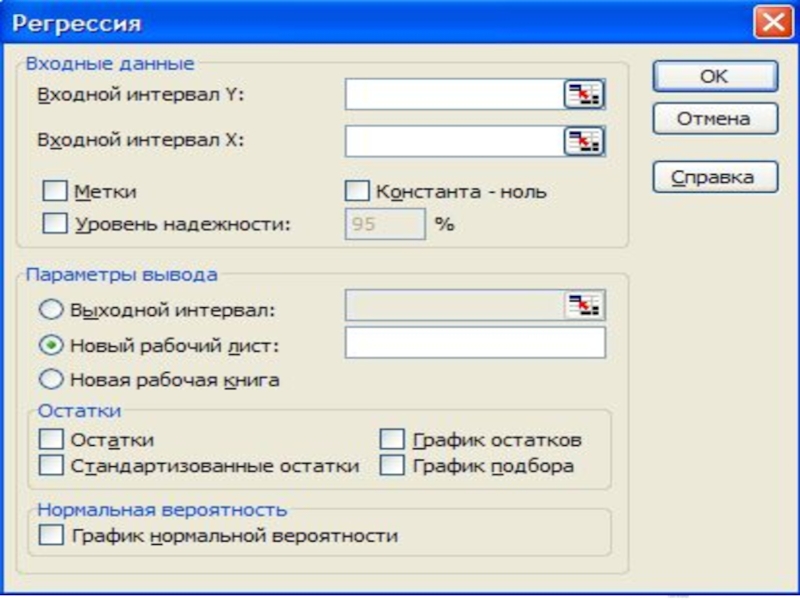
Расчет показателей регрессии и корреляции с помощью пакета анализа в
Excel
Установка пакета анализа:
Кнопка «Office»
Параметры Excel
Надстройки
Надстройки Excel
Перейти
Пакет анализа
После установки пакета анализа:
Данные
Анализ
данных
Регрессия
Слайд 59
Расчет показателей регрессии и корреляции с помощью пакета анализа в
Excel
В диалоговом окне «регрессия» задаются следующее параметры:
-Входной интервал Y, -
водится ссылка на диапазон ячеек, содержащий данные результативного признака
Входной интервал X, - водится ссылка на диапазон ячеек, содержащий данные факторного признака
-Если данные выделяются с названием граф, то устанавливается флажок метки
-Параметры вывода: выходной интервал (вводится ссылка на любую свободную ячейку на данном рабочем листе); другой рабочий лист или другая рабочая книга
-ОК
Слайд 61
Использование модели парной регрессии для прогнозирования
Слайд 66
Свойства остатков
Отсутствие связи между остатками и объясняющей переменной
Отсутствие связи между
остатками и предсказанными значениями
Математическое ожидание остатков равно нулю
Остатки имеют
постоянную дисперсию. Дисперсия остатков равна единице. Постоянство дисперсии остатков называют гомоскедастичностью остатков. Если же дисперсия остатков непостоянна, то имеет место гетероскедастичность остатков
Остатки не коррелированны между собой
Остатки распределены по нормальному закону распределения
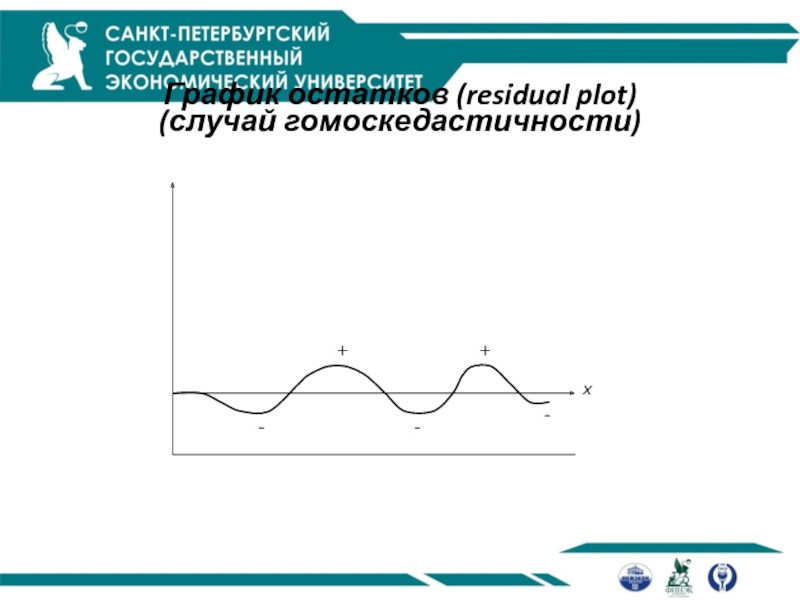
Слайд 67
График остатков (residual plot)
(случай гомоскедастичности)
Слайд 68
Зависимость остатков от выровненного значения результата

![ЭКОНОМЕТРИКА Основная литератураЭконометрика: учебник для магистрантов / И.И. Елисеева [и др.]; Основная литератураЭконометрика: учебник для магистрантов / И.И. Елисеева [и др.]; под ред. И.И.Елисеевой. ‑ М.:](/img/thumbs/8e2e26a0a21843cfd4be885c8b8a0f39-800x.jpg)