Электродинамические усилия (ЭДУ) в электрических аппаратах

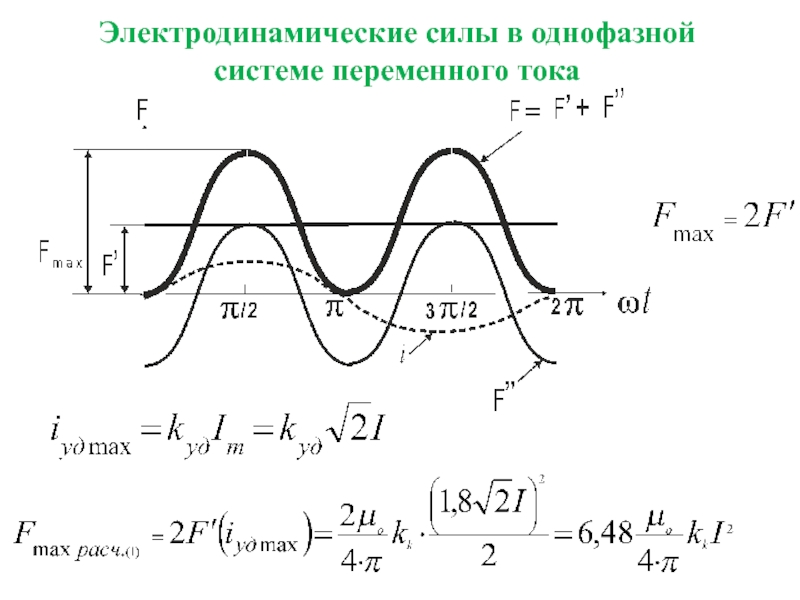
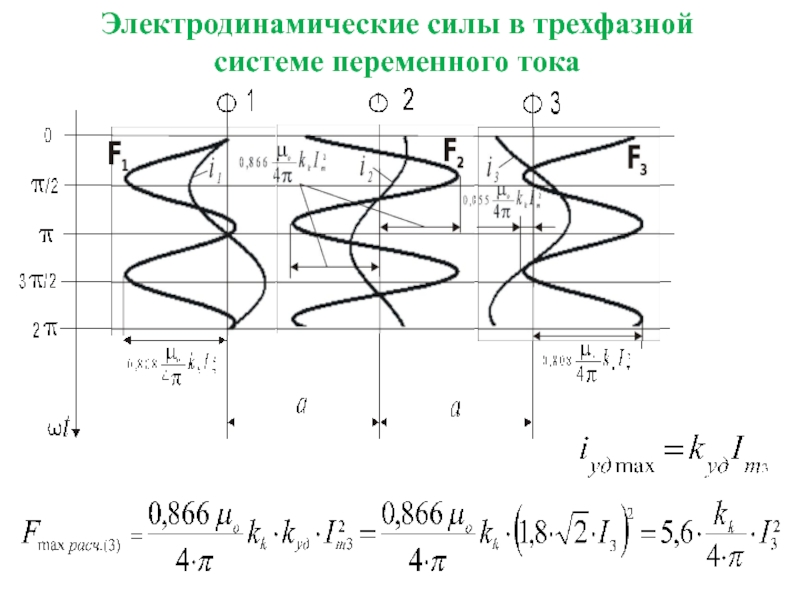
противостоять ЭДУ (механическим воздействиям), возникающим при прохождении сквозных токов КЗ. 
Она

выражается либо амплитудным значением тока iдин,
либо кратностью этого тока относительно амплитуды номинального тока Iном, т.е
kдин = iдин /√2 Iном.

Иногда действующим значением ударного тока за период после начала КЗ (Iуд).

содержат четыре составляющие:
1) постоянную составляющую;
2)периодическую составляющую, меняющуюся с двойной

промышленной частотой от взаимодействия периодических составляющих тока;
3) непериодическую составляющую с частотой 50 Гц от взаимодействия периодической составляющей тока в одном проводнике и свободной составляющей в другом проводнике;
4) апериодическую составляющую от взаимодействия свободных составляющих тока. 

(механические напряжения), которые могут: деформировать или разрушить обмотки; токоведущие части

и опорные конструкции ЭА; изоляторы, с помощью которых проводники укреплены к заземленным частям аппарата и др. 

Электродинамические силы пропорциональны квадрату тока и могут превысить более чем в 4000 раз соответствующие нормальные значения. В сильноточных аппаратах электродинамические силы могут достигать десятков тысяч Ньютон.

Влияние электродинамических сил при включении на существующее короткое замыкание сказывается в большей степени, чем при отключении.

током и магнитного поля (индукции) по правилу Ампера.

Применяется тогда, когда можно определить аналитически индукцию в любой точке проводника, для которого необходимо определить силу (F).
2. Основан на использовании энергетического баланса
системы проводников с током, т.е. на изменении запаса магнитной энергии токоведущего контура.
Применяется тогда, когда известны аналитические зависимости (формулы), связывающие индуктивность и взаимоиндуктивность контуров с их геометрическими параметрами, т.е. в витках и катушках ЭА.

i dl х B = iBdlsinβ
На элементарный проводник длиной dl,

с током i, находящийся в магнитном поле с индукцией В, созданной другим проводником действует усилие

β – угол между векторами элемента dl и индукцией B, измеряемый по кратчайшему расстоянию между ними. За направление dl принимается направление тока в элементе.

B определяется по закону Био-Савара-Лапласа.

При β=900 F = = В*I*L

проводнику l2

> 0, т.е. сила F, действующая на токоведущие части, направлена

так, чтобы электромагнитная энергия системы возрастала.

Сила взаимодействия двух взаимосвязанных контуров

Энергия для двух контуров

а – расстояние между проводниками с токами i1 и i2

l2 с любым сдвигом

т.к. магнитные силовые линии вокруг проводников представляют собой окружности и

можно считать, что ток сосредоточен в геометрической оси проводника.
Поверхностный эффект в проводниках круглого сечения не сказывается на ЭДУ, а эффект близости, смещающий токи в проводниках, вызывает увеличение ЭДУ при встречных токах и уменьшение – при согласованных.

силовые линии около провод-ников являются не окружностями, а овалами. Это

влияние учитывается с помощью кривых Двайта, по которым находится коэффициент формы kф, после чего ЭДУ находится по формуле

Fx = 10-7i1i2 kkф

dx
dFx = iBxdx
Индукция от проводника h → ∞ в

точке на расстоянии х от его оси
Bx = μ0i /4πx

при h конечном

Fх = 10-7i2 ln a/r

на проводник конечной длины l1

,

Если l2 конечной длины, то полная сила, действующая на проводник конечной длины l1

действующая на виток
Электродинамическая сила Fx, стремящаяся разорвать виток

r
R

i

r1

r2

F1

F2

B

F2 = μ0 i2 ln r2/r1 = 10-7 i2 ln r2/r1
4π

Электродинамические усилия в месте изменения сечения

Электродинамическая сила F, возникающая при изменении сечения, зависит только от отношения радиусов (сечений) и не зависит от длины и формы перехода, направления токов.

сила, действующая по оси проводника
Для некруглого сечения

по закону
Iт – амплитудное значение.
Учитывая, что sin2t =

(1 – cos 2t)/2, мгновенное значение электродинамической силы между отдельными частями проводника