Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия и методы теории вероятностей
Содержание
- 1. Основные понятия и методы теории вероятностей
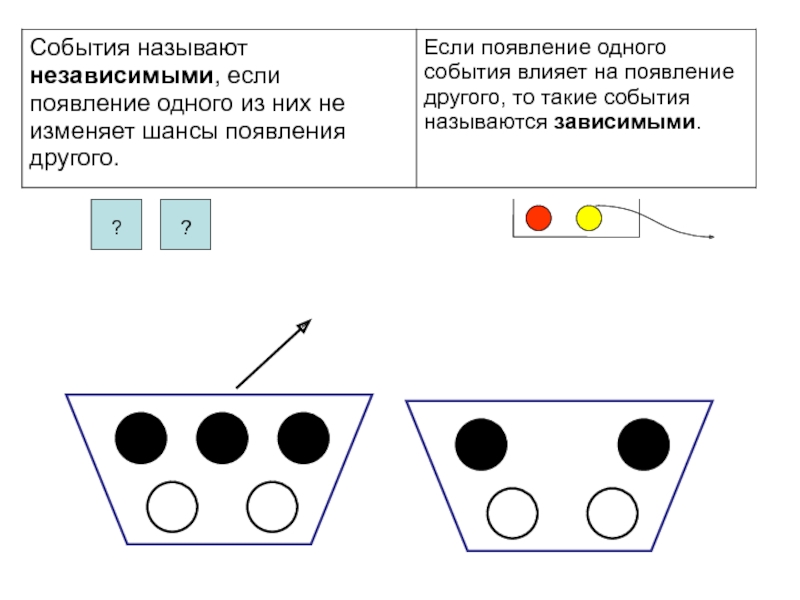
- 2. События Детерминированные – о которых точно известно,
- 3. Астрономия Метеорология
- 4. В окружающей действительности имеется множество случайных явлений, подчиняющихся законам, проявляющимся при большом числе наблюдений.
- 5. Теория вероятностей – раздел математики, изучающий
- 6. Из истории теории вероятностей Основы теории вероятностей
- 7. Современная теория вероятностей основана на аксиоматическом подходе
- 8. Эксперимент, опыт или наблюдение называют
- 9. Определение Случайным событием называется результат
- 10. Слайд 10
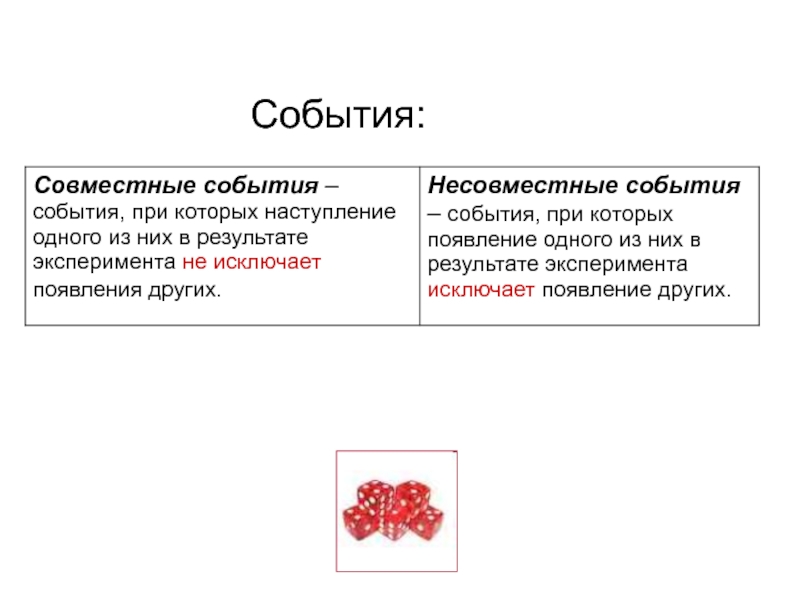
- 11. События:
- 12. Слайд 12
- 13. Отдельный исход испытания называют элементарным событием, например,
- 14. Определение Пространством элементарных событий называют множество
- 15. Случайным событием называют любое подмножество А
- 16. Полная группа событий {A1, A2, ..., Аn}
- 17. Какие из перечисленных
- 18. Противоположные события, произведение событий, Алгебра случайных событий и теория множествАUВ=ØСумма событий
- 19. Суммой двух событий и называется
- 20. ЗадачаВ урне 5 красных, 2 синих, 3
- 21. Понятие вероятности случайного событияВероятность – количественная мера
- 22. Для двух событий…1.Вероятность достоверного события Р(Ω)=1. 2.Вероятность
- 23. Аксиоматическое определение вероятности Вероятностью P(A)
- 24. Тройка ( , F , P), где
- 25. Классическая вероятность – это вероятность, базирующаяся на
- 26. Вероятность появления события А – это отношение
- 27. ЗадачаВ урне находятся 2 белых и 3
- 28. Относительная частота – результат многократных испытаний. С
- 29. Геометрическое определение вероятностиВероятность события А – «точка попадает в область d» равнаdD
- 30. Алгоритм решения задач определения вероятности события:Определить состав
- 31. Задача 1 Последовательно бросили
- 32. РешениеР(В)= ? При бросании
- 33. Решение При бросании возможно 36=6*6
- 34. Задача 2 В ящике
- 35. 2 – крас., 2 – бел.,
- 36. Сколько исходов благоприятных событию А «вынуты два
- 37. Число исходов благоприятных событию В (два синих
- 38. Задача 3 В урне было
- 39. Задача 4 Из 10 студентов,
- 40. Теорема сложения вероятностейДля совместных событийВероятность суммы попарно
- 41. Например: В лотерее выпущено 10
- 42. РешениеА – «человек выиграл не менее 25
- 43. Слайд 43
- 44. Теорема умножения вероятностейВероятность произведения двух зависимых событий
- 45. Задача. Студент пришел на экзамен, изучив только
- 46. Вероятность появления хотя бы одного события Вероятность
- 47. Формула полной вероятности Пусть требуется определить
- 48. Пусть имеется полная группа несовместных гипотез:А1, А2,
- 49. Формула БайесаСогласно теореме умножения вероятностей,P(AiK) = P(Ai)PAi(K) и P(AiK)
- 50. Н(а) - энтропия мера объективной неопределенности.Н(а)
- 51. Задача.В сосуде 10 шаров, из них n
- 52. n – белые (10-n)
- 53. Нn010H(a)=- log
- 54. Н(а) = -ΣРi log PiP=1/16Н(а) = 4
- 55. 0 1 2 3 4 5 6
- 56. Теорема сложения вероятностейДля совместных событийВероятность суммы попарно
- 57. Задача В лотерее выпущено 10
- 58. Задача В лотерее выпущено 10
- 59. Теорема умножения вероятностейВероятность произведения двух зависимых событий
- 60. Задача. Студент пришел на экзамен, изучив только
- 61. Вероятность появления хотя бы одного события Вероятность
- 62. Формула полной вероятности
- 63. Пример
- 64. ПримерА1 – выбор первой урны, А2 –
- 65. Формула полной вероятностиПусть требуется определить вероятность некоторого
- 66. ДоказательствоТак как гипотезы А1, А2, …, Аn
- 67. Задача 1По самолету производится три одиночных выстрела.
- 68. РешениеРассмотрим четыре гипотезы:А0 – в самолет не
- 69. РешениеСобытие К – выход самолета из строяУсловные
- 70. Задача 2В первой урне содержится 10 шаров,
- 71. Решение
- 72. Скачать презентанцию
События Детерминированные – о которых точно известно, что причина приведет к определенному следствию.Случайные – в которых исход непредсказуем.
Слайды и текст этой презентации
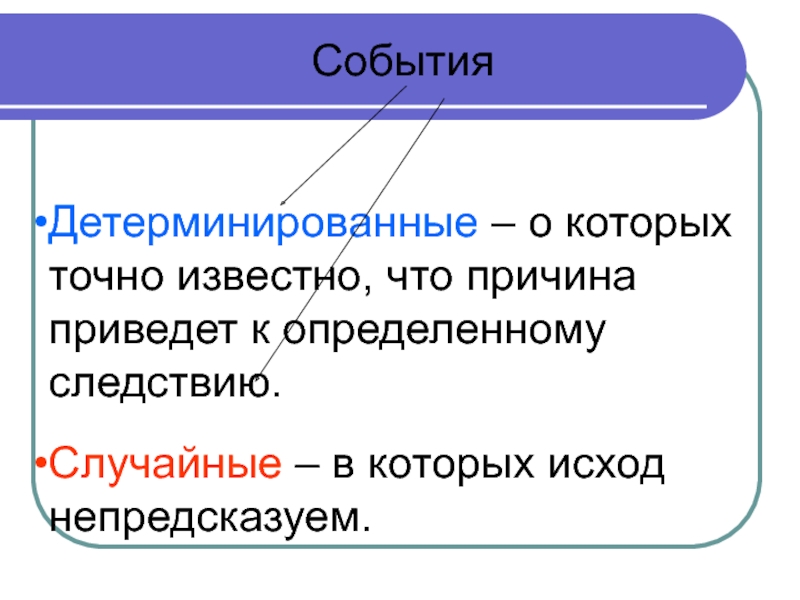
Слайд 2События
Детерминированные – о которых точно известно, что причина приведет
к определенному следствию.
Слайд 4В окружающей действительности имеется множество случайных явлений, подчиняющихся законам, проявляющимся
при большом числе наблюдений.
Слайд 5
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений и
событий, способных многократно повторяться при воспроизведении определенного комплекса условий.
Основная задача
теории вероятностей – установление математических законов для исследования случайных величин массового характера и предвидения их на основании отдельных фактов. В теории вероятностей изучаются модели экспериментов, результаты которых нельзя предсказать заранее.
«эксперимент» = «опыт» = «испытание»
«результаты» =«исходы»
Слайд 6Из истории теории вероятностей
Основы теории вероятностей заложены:
В 16-18
вв. Б. Паскалем, Ферма, Г. Галилеем, Я. Бернулли, П.С. Лапласом,
Муавром и др.В 19 в. внесены современные идеи российскими учеными: П.Л. Чебышевым и его учениками А.А. Марковым и А.М. Ляпуновым.
В 20 в. вклад в развитие теории вероятностей внесли российские математики: С.Н. Бернштейн, Б.В. Гнеденко, А.Н. Колмогоров, B.C. Пугачев, В.И. Романовский, Н.В. Смирнов, А.Я. Хинчин и др.
Слайд 7Современная теория вероятностей основана на аксиоматическом подходе Колмогорова.
Практическое значение вероятностных
методов – по известным характеристикам простых случайных явлений прогнозировать характеристики
более сложных явлений.
Слайд 8 Эксперимент, опыт или наблюдение называют испытанием.
Результат (исход)
эксперимента называют событием.
Например.
Извлечение карты из колоды – испытание.
Исход испытания – извлечение дамы бубен.
Условие испытания - число карт в колоде (36 или 52).
Слайд 9Определение
Случайным событием называется результат испытания (или наблюдения),
который при данном испытании может произойти, а может и не
произойти.
Слайд 13Отдельный исход испытания называют элементарным событием, например, извлечение любой карты
из колоды.
Набор всех элементарных событий называют пространством событий, или полной
группой событий.например, 36 или 52 карты.
Слайд 14Определение
Пространством элементарных событий называют множество Ω взаимоисключающих исходов
эксперимента такое, что каждый интересующий результат эксперимента может быть однозначно
описан с помощью элементов этого множества.Элементы Ω называются элементарными событиями и обозначаются .
Слайд 15Случайным событием называют любое подмножество А Ω элементов из
Ω.
Событие А произойдет, если произойдет какое-либо событие из элементарных событий
А
Слайд 16Полная группа событий {A1, A2, ..., Аn} – совокупность единственно
возможных и несовместных = Ω и
∩Аj =Ø для любой пары (i j) событий.Полная группа событий
Слайд 17
Какие из перечисленных событий являются
достоверными?
Замерзшая вода при сильном морозе
После мая всегда идет июнь
Попадание дротиком
с первого разаВыпадение 7 очков при игре в кости
Слайд 18
Противоположные события, произведение событий,
Алгебра случайных событий
и теория множеств
АUВ=Ø
Сумма событий
Слайд 19Суммой двух событий и называется событие +
, состоящее из элементарных событий, принадлежащих хотя бы одному из
событий или .Произведением двух событий и называется событие , состоящих из элементарных событий, принадлежащих одновременно и .
Противоположным событием событию называют событие , состоящее из элементарных событий, не принадлежащих .
Разностью двух событий и называют событие \, состоящее из элементарных событий, которые входят в событие .
Слайд 20Задача
В урне 5 красных, 2 синих, 3 белых шара. Все
они пронумерованы цифрами 1,2,…,10. Из урны берется наудачу 1 шар.
Обозначим события :А – шар оказался с четным номером,
В – с номером кратным 3,
С – шар красного цвета,
Д – шар синего цвета,
Е – шар белого цвета.
Что представляют собой события:
АВ; С+Е; АД; А-В;
Слайд 21Понятие вероятности случайного события
Вероятность – количественная мера неопределенности, выражающая степень
уверенности в наступлении события.
Вероятность – число Р(А)[0;1], характеризующее степень возможности
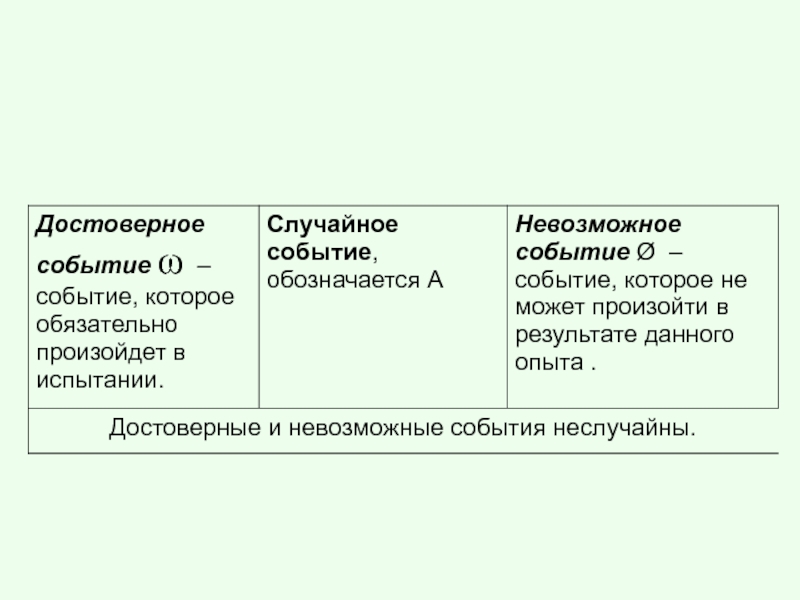
появления события А.![Понятие вероятности случайного событияВероятность – количественная мера неопределенности, выражающая степень уверенности в наступлении события.Вероятность – число Р(А)[0;1],](/img/thumbs/fb779b48a259268b01f667949c23a262-800x.jpg "Основные понятия и методы теории вероятностей Понятие вероятности случайного событияВероятность – количественная мера неопределенности, выражающая степень уверенности")
Слайд 22Для двух событий…
1.Вероятность достоверного события Р(Ω)=1.
2.Вероятность невозможного события Р(Ø)=0.
3.Вероятность случайного события 0≤P(A)≤1.
4.Сумма вероятностей противоположных событий
Р(А)+Р(Ā)=1.
Слайд 23Аксиоматическое определение вероятности
Вероятностью P(A) называется числовая функция,
определенная на всех F и удовлетворяющая трем условиям
(аксиомам вероятностей):P(A) 0;
P()=1;
Для любой конечной или бесконечной последовательности наблюдаемых событий
таких, что при
Слайд 24Тройка ( , F , P), где
-
множество элементарных событий
F – множество всех подмножеств
P
– множество вероятностей случайных событий,называется вероятностным пространством (это понятие введено А.Н. Колмогоровым)
Слайд 25
Классическая вероятность – это вероятность, базирующаяся на симметричной игре шансов
или одинаковых ситуациях и исходящая из равновозможности определенных явлений.
Слайд 26Вероятность появления события А – это отношение числа исходов, благоприятствующих
наступлению события, к общему числу всех единственно возможных и несовместных
элементарных исходов.Р(А)= ,
где 0 ≤ М ≤ N – целое неотрицательное число благоприятствующих событию А исходов, N – число всех исходов.
Классическое определение вероятности
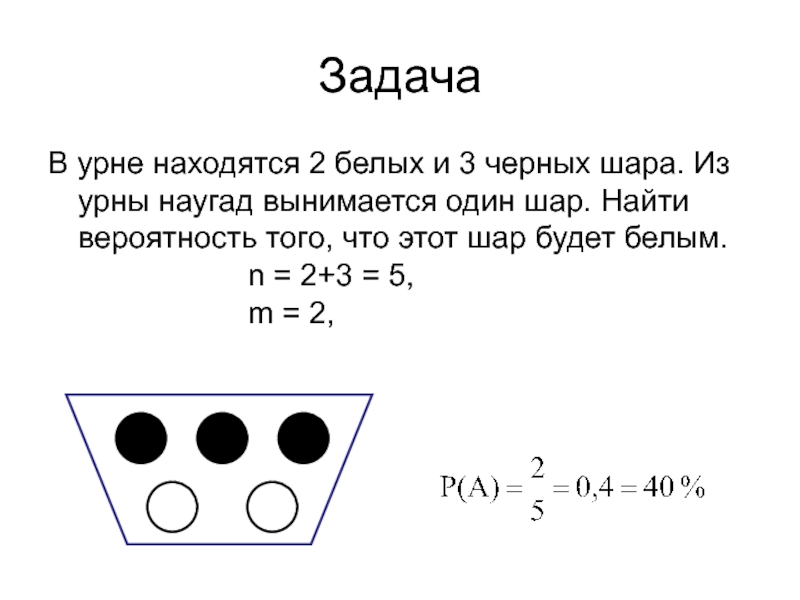
Слайд 27Задача
В урне находятся 2 белых и 3 черных шара. Из
урны наугад вынимается один шар. Найти вероятность того, что этот
шар будет белым.n = 2+3 = 5,
m = 2,
Слайд 28Относительная частота – результат многократных испытаний. С увеличением числа испытаний
относительная частота проявляет тенденцию стабилизироваться, проявляет устойчивость.
Статистическая вероятность события
А – частотность события, вычисленная по результатам большого числа испытанийР*(А)≈Р(А)
(обосновано в законе больших чисел Я.Бернулли)
Статистическое определение вероятности
Слайд 29Геометрическое определение вероятности
Вероятность события А – «точка попадает в область
d» равна
d
D
Слайд 30Алгоритм решения задач определения
вероятности события:
Определить состав эксперимента.
Определить элементарное событие
в эксперименте.
Определить полную группу событий, найти число событий в группе.
Определить
интересующее нас событие, найти их число в опыте.Найти вероятность события по формуле.
Слайд 31Задача 1
Последовательно бросили две игральные кости.
Какова вероятность события В – «при бросании костей в сумме
выпало 8 очков», и вероятность события С – «при бросании в сумме выпало 12 очков».Решение
Состав эксперимента: бросили две игральные кости. Результаты эксперимента: Элементарные события выпадение на двух кубиках некоторого количества очков. Полная группа событий выпадение на двух кубиках (1,1), (1,2), (1,3), … , (6,6)
Событие В – в сумме выпало 8 очков
Событие С – в сумме выпало 12 очков
Слайд 32Решение
Р(В)= ?
При бросании возможно 36=6*6 равновозможных
элементарных исходов.
Событию В благоприятны 5 исходов
2+6,
3+5, 4+4, 5+3, 6+2Р(В)=5/36
Слайд 33Решение
При бросании возможно 36=6*6 равновозможных элементарных исходов.
Один благоприятствующий исход 6+6=12 очков.
Р(С)= 1/36
Слайд 34Задача 2
В ящике имеются два красных,
два белых и шесть синих шаров. Наудачу вынимаем два шара.
Какова вероятность событийА – «вынуты два красных шара» и
В – «вынуты два синих шара»?
Слайд 352 – крас., 2 – бел., 6 – син.
Всего - 10 шаров
Число всех равновозможных исходов испытания
равно количеству комбинаций из 10 по 2. С=45
Слайд 36Сколько исходов благоприятных событию А «вынуты два красных шара»?
событию А благоприятствует один исход, т.к. красных шаров –
два.Р(А)=1/45
Слайд 37Число исходов благоприятных событию В (два синих шара) равно количеству
комбинаций из 6 по 2.
С=15
Р(В)=15/45=1/3
Слайд 38Задача 3
В урне было 5 шаров черного
и 3 шара белого цвета. Один шар был вытащен (цвет
его неизвестен). Затем вытащили еще два шара.Какова вероятность того, что оба шара белые? (Ответ записать в виде обыкновенной дроби).
Слайд 39Задача 4
Из 10 студентов, среди которых 4
юноши, случайным образом выбирают 5 человек для участия в игре.
Какова вероятность, что среди выбранных студентов будут 2 юноши?
Слайд 40Теорема сложения вероятностей
Для совместных событий
Вероятность суммы попарно несовместных событий равна
сумме вероятностей этих событий P(A1+A2)=P(A1)+P(A2)
Для несовместных событий
Вероятность суммы
двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:P(A+B)=P(A)+P(B)–P(AB)
Слайд 41Например:
В лотерее выпущено 10 000 билетов и
установлено:
10 выигрышей по 200 руб.
100 выигрышей по 100 руб.
500 выигрышей
по 25 руб.1000 выигрышей по 5 руб.
Какова вероятность того, что человек, купивший билет, выиграет не менее 25 руб.?
Слайд 42Решение
А – «человек выиграл не менее 25 руб.?»
В – «человек
выиграл 200 руб.?»
С – «человек выиграл 100 руб.?»
D - «человек
выиграл 25 руб.?»P(A)=P(В+С+D)=P(B)+P(C)+P(D)= =10/10000+100/10000+500/10000==0,061.
Слайд 44Теорема умножения вероятностей
Вероятность произведения двух зависимых событий А, В равна
произведению вероятности одного из них на условную вероятность другого Р(АВ)
= Р(В)∙Р(А/В) = Р(A)∙Р(B/A).
Слайд 45Задача. Студент пришел на экзамен, изучив только 20 из 25
вопросов программы. Экзаменационный билет содержит три вопроса. Вычислить вероятность того,
что студент ответит на все три вопроса (событие А).Решение. Определим события:
А – «студент знает три вопроса билета»;
A1 – «студент знает 1-ый вопрос билета»;
А2 – «студент знает 2-ой вопрос билета»;
А3 – «студент знает 3-ий вопрос билета».
События A1, А2, А3 – зависимые:
P(A)=P(А1)·P(A2/A1)·P(A3/A1·A2)=
=(20/25)·(19/24)·(18/23)=57/115=0,496.
Слайд 46Вероятность появления хотя бы одного события
Вероятность появления хотя бы одного
события из n независимых в совокупности равна разности между 1
и произведением вероятностей противоположных событий
Слайд 47Формула полной вероятности
Пусть требуется определить вероятность некоторого события
К, которое может произойти вместе с одним из событий А1,
А2, …, Аn, образующих полную группу несовместных событий. Эти события называются гипотезами.Формула полной вероятности:
P(K) = P(A1)PA1(K) + P(A2)PA2(K) + … + P(An)PAn(K)
или
Слайд 48Пусть имеется полная группа несовместных гипотез:
А1, А2, …, Аn
Вероятности этих
гипотез до проведения опыта известны и равны соответственно:
P(А1), P(А2), …,
P(Аn)Произведен опыт, в результате которого наступило некоторое событие К.
Спрашивается, как изменятся вероятности гипотез в связи с появлением этого события?
То есть необходимо найти условную вероятность PK(Ai) для каждой гипотезы Ai.
PK(Ai) – ?
Слайд 49Формула Байеса
Согласно теореме умножения вероятностей,
P(AiK) = P(Ai)PAi(K) и P(AiK) = P(K)PK(Ai)
P(Ai)PAi(K) =
P(K)PK(Ai)
Подставляя P(K) по формуле полной вероятности, получим Формулу Байеса (или
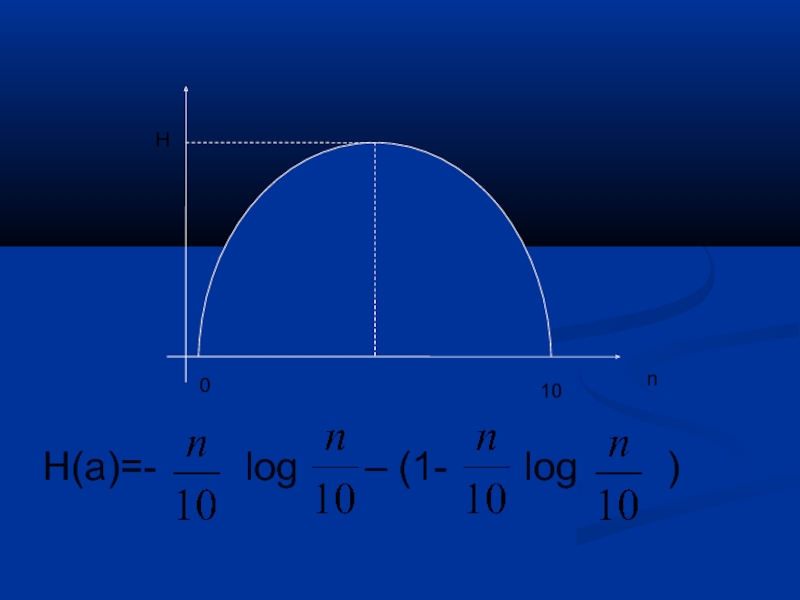
теорему гипотез):
Слайд 50Н(а) - энтропия
мера объективной неопределенности.
Н(а) = -ΣРi log Pi
где
а – элементарное событие, Р – вероятность события, i =
1, … nДля опыта с двумя возможными исходами
H(a)= - P1 logP1 – P2 log P2,
Р1 и Р2 в этом выражении – вероятности отдельных исходов а1 и а2 эксперимента а.
H(a)= 1
Слайд 51Задача.
В сосуде 10 шаров, из них n – белые,
10-n
– черные. Из сосуда вынимают один шар. Возможные исходы этого
эксперимента – вынутый шар белый или черный.Как выражается неопределенность в предсказании цвета вынимаемого шара.
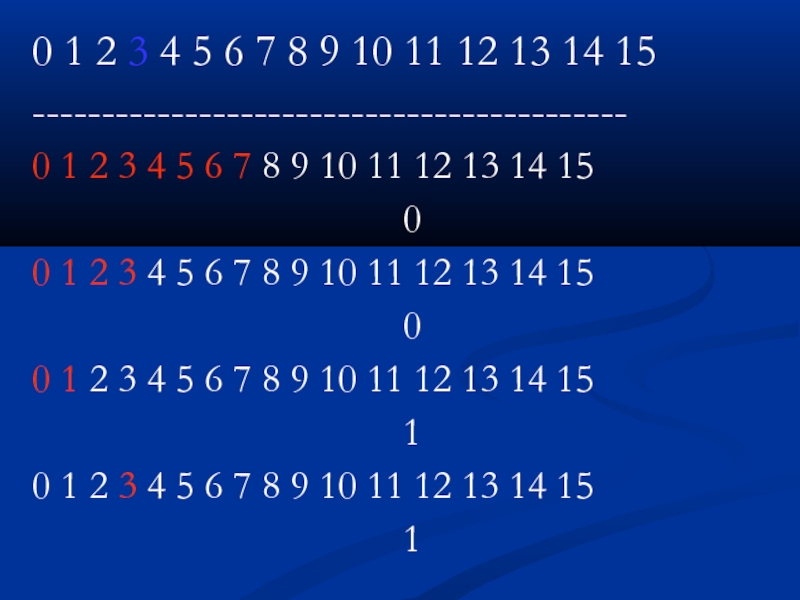
Слайд 550 1 2 3 4 5 6 7 8 9
10 11 12 13 14 15
-------------------------------------------
0 1 2 3
4 5 6 7 8 9 10 11 12 13 14 150
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1
Слайд 56Теорема сложения вероятностей
Для совместных событий
Вероятность суммы попарно несовместных событий равна
сумме вероятностей этих событий P(A1+A2)=P(A1)+P(A2)
Для совместных событий
Вероятность суммы
двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления:P(A+B)=P(A)+P(B)–P(AB)
Слайд 57Задача
В лотерее выпущено 10 000 билетов и
установлено:
10 выигрышей по 200 руб.
100 выигрышей по 100 руб.
500 выигрышей
по 25 руб.1000 выигрышей по 5 руб.
Какова вероятность того, что человек, купивший билет, выиграет не менее 25 руб.?
Слайд 58Задача
В лотерее выпущено 10 000 билетов и
установлено:
10 выигрышей по 200 руб.
100 выигрышей по 100 руб.
500 выигрышей
по 25 руб.1000 выигрышей по 5 руб.
Какова вероятность того, что человек, купивший билет, выиграет не менее 25 руб.?
Решение
А – «человек выиграл не менее 25 руб.?»
В – «человек выиграл 200 руб.?»
С – «человек выиграл 100 руб.?»
D - «человек выиграл 25 руб.?»
P(A)=P(В+С+D)=P(B)+P(C)+P(D)= 10/10000+100/10000+500/10000=0,061.
Слайд 59Теорема умножения вероятностей
Вероятность произведения двух зависимых событий А, В равна
произведению вероятности одного из них на условную вероятность другого Р(АВ)=Р(В)∙Р(А/В)=Р(A)∙Р(B/A).
Пример. Консультационная фирма претендует на два заказа от двух корпораций. Эксперты фирмы считают, что вероятность получения заказа в корпорации А (событие А) равна 0,45. Эксперты также полагают, что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратится к ним, равна 0,9. Какова вероятность получения фирмой обоих заказов?
Решение. Согласно условиям Р(А)=0,45, Р(В/А)=0,9.
Необходимо найти P(AB), которая является вероятностью того, что оба события (и событие А, и событие В) произойдут.
Р(АВ)=Р(А)∙Р(В/А)=0,45∙0,9=0,405.
Слайд 60Задача. Студент пришел на экзамен, изучив только 20 из 25
вопросов программы. Экзаменационный билет содержит три вопроса. Вычислить вероятность того,
что студент ответит на все три вопроса (событие А).Решение. Определим события:
А – «студент знает три вопроса»;
A1 – «студент знает 1-ый вопрос»;
А2 – «студент знает 2-ой вопрос»;
А3 – «студент знает 3-ий вопрос».
События A1, А2, А3 – зависимые:
P(A)=P(А1)·P(A2/A1)·P(A3/A1·A2)=
=(20/25)·(19/24)·(18/23)=57/115=0,496.
Слайд 61Вероятность появления хотя бы одного события
Вероятность появления хотя бы одного
события из n независимых в совокупности равна разности между 1
и произведением вероятностей противоположных событий
Слайд 64Пример
А1 – выбор первой урны, А2 – выбор второй урны,
А3 – выбор третьей урны, К – появление белого шара.
P(A1)
= P(A2) = P(A3) = 1/3PA1(K) = 2/3; PA2(K) = 3/4; PA3(K) = ½
K = A1K + A2K + A3K
P(K) = P(A1K) + P(A2K) + P(A3K)
P(K) = P(A1)PA1(K) + P(A2)PA2(K) + P(A3)PA3(K)
Слайд 65Формула полной вероятности
Пусть требуется определить вероятность некоторого события К, которое
может произойти вместе с одним из событий А1, А2, …,
Аn, образующих полную группу несовместных событий. Эти события называются гипотезами.Формула полной вероятности:
P(K) = P(A1)PA1(K) + P(A2)PA2(K) + … + P(An)PAn(K)
или
Слайд 66Доказательство
Так как гипотезы А1, А2, …, Аn образуют полную группу,
то событие К может появиться только в комбинации с какой-либо
из этих гипотез, то есть:К = А1К + А2К + … + АnК.
Так как гипотезы А1, А2, …, Аn несовместны, то и комбинации А1К, А2К, …, АnК также несовместны. Поэтому к ним можно применить теорему сложения вероятностей:
P(K) = P(A1K) + P(A2K) + … + P(AnK)
Слайд 67Задача 1
По самолету производится три одиночных выстрела. Вероятность попадания при
первом выстреле равна 0,4; при втором – 0,5; при третьем
– 0,7.Для вывода самолета из строя достаточно трех попаданий. При одном попадании самолет выходит из строя с вероятностью 0,2; при двух попаданиях – с вероятностью 0,6.
Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.
Слайд 68Решение
Рассмотрим четыре гипотезы:
А0 – в самолет не попало ни одного
снаряда,
А1 – в самолет попал один снаряд,
А2 – в самолет
попало два снаряда,А3 – в самолет попало три снаряда.
P(A0) = 0,6 0,5 0,3 = 0,09
P(A1) = 0,40,50,3 + 0,60,50,3 + 0,60,50,7 = 0,06 + 0,09 + 0,21 = 0,36
P(A2) = 0,40,50,3 + 0,40,50,7 + 0,60,50,7 = 0,06 + 0,14 + 0,21 = 0,41
P(A3) = 0,4 0,5 0,7 = 0,14
Слайд 69Решение
Событие К – выход самолета из строя
Условные вероятности события К
при этих гипотезах равны:
PA0(K) = 0; PA1(K) = 0,2; PA2(K) = 0,6; PA3(K)
= 1.P(K) = P(A0)PA0(K) + P(A1)PA1(K) + P(A2)PA2(K) + P(A3)PA3(K)
P(K) = 0,090 + 0,360,2 + 0,410,6 + 0,141 = 0 + 0,072 + 0,246 + 0,140 = 0,458
Слайд 70Задача 2
В первой урне содержится 10 шаров, из них 8
– белые; во второй урне 20 шаров, из них 4
– белые.Из каждой урны наугад извлекли по одному шару, а затем из этих двух шаров наугад выбрали 1 шар. Найти вероятность того, что был взят белый шар.
