TheSlide.ru

Параллелепипед

Содержание

1. Параллелепипед
2. Параллелограммы, из которых состоит параллелепипед называются гранями
3. Стороны параллелограммы, из которых состоит параллелепипед называются
4. Вершины параллелограммы, из которых состоит параллелепипед называются
5. Грани, имеющие общее ребро называются смежнымиГрани, не
6. Свойства параллелепипеда: 10 Противоположные грани параллелепипеда
7. 20 Диагонали параллелепипеда пересекаются в одной
8. Скачать презентанцию

Параллелограммы, из которых состоит параллелепипед называются гранями параллелепипеда. Параллелепипед имеет 6 гранейABCD, A1B1C1D1, AA1B1B, BB1C1C, DD1C1C, AA1D1D C1C

Слайды и текст этой презентации

Слайд 1Параллелепипед Поверхность, составленная из шести попарно равных параллелограммов называется параллелепипедом

Параллелепипед Поверхность, составленная из шести попарно равных параллелограммов называется параллелепипедом

Слайд 2Параллелограммы, из которых состоит параллелепипед называются гранями параллелепипеда.
Параллелепипед имеет 6

граней

ABCD, A1B1C1D1, AA1B1B, BB1C1C, DD1C1C, AA1D1D
C1
C

Параллелограммы, из которых состоит параллелепипед называются гранями параллелепипеда. Параллелепипед имеет 6 гранейABCD, A1B1C1D1, AA1B1B, BB1C1C, DD1C1C,

Слайд 3Стороны параллелограммы, из которых состоит параллелепипед называются рёбрами параллелепипеда
Параллелепипед имеет

12 ребер

AB, BC, CD, DA, AA1, A1D1, D1D, D1C1, C1B1,

B1A1 B1B, C1C

C1

C

Стороны параллелограммы, из которых состоит параллелепипед называются рёбрами параллелепипедаПараллелепипед имеет 12 реберAB, BC, CD, DA, AA1, A1D1,

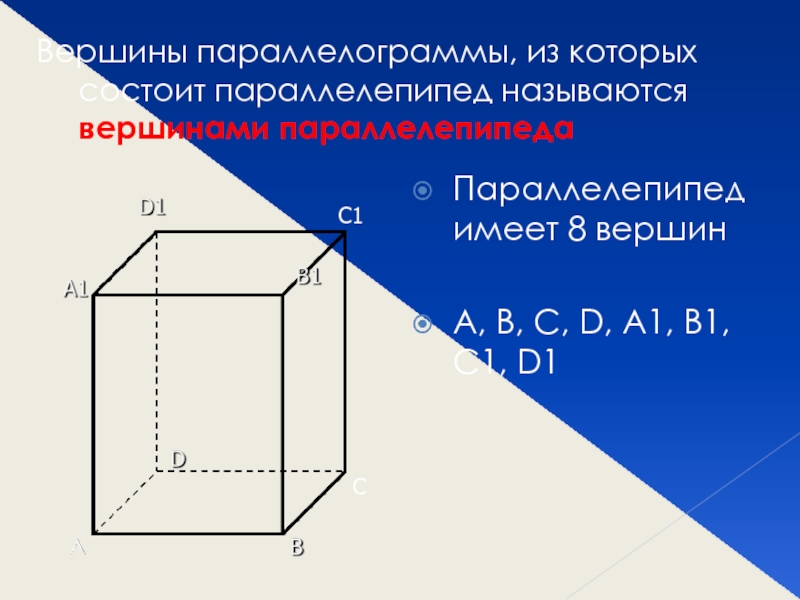
Слайд 4Вершины параллелограммы, из которых состоит параллелепипед называются вершинами параллелепипеда
Параллелепипед имеет

8 вершин

A, B, C, D, A1, B1, C1, D1
C1
C

Вершины параллелограммы, из которых состоит параллелепипед называются вершинами параллелепипедаПараллелепипед имеет 8 вершинA, B, C, D, A1, B1,

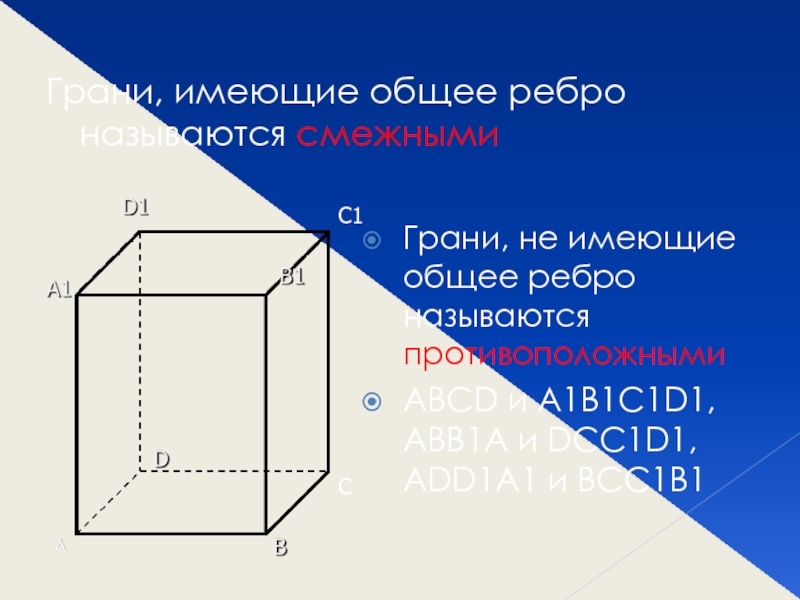
Слайд 5Грани, имеющие общее ребро называются смежными

Грани, не имеющие общее ребро

называются противоположными
ABCD и A1B1C1D1, ABB1A и DCC1D1, ADD1A1 и BCC1B1
C1
C

Грани, имеющие общее ребро называются смежнымиГрани, не имеющие общее ребро называются противоположнымиABCD и A1B1C1D1, ABB1A и DCC1D1,

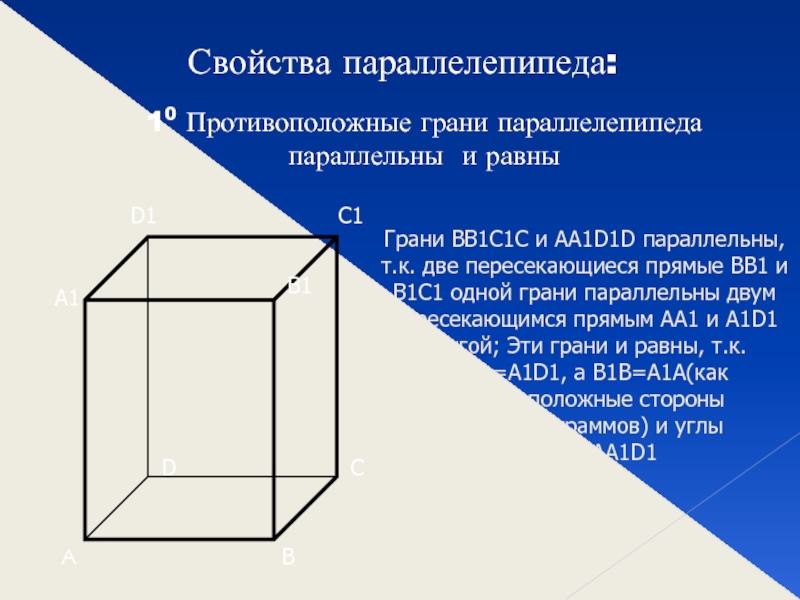
Слайд 6Свойства параллелепипеда: 10 Противоположные грани параллелепипеда параллельны и равны

A
B
D
C
C1
D1
A1
B1
Грани BB1C1C и

AA1D1D параллельны, т.к. две пересекающиеся прямые BB1 и B1C1 одной

грани параллельны двум пересекающимся прямым AA1 и A1D1 другой; Эти грани и равны, т.к. B1C1=A1D1, а B1B=A1A(как противоположные стороны параллелограммов) и углы BB1C1=AA1D1

Свойства параллелепипеда: 10 Противоположные грани параллелепипеда параллельны и равныABDCC1D1A1B1Грани BB1C1C и AA1D1D параллельны, т.к. две пересекающиеся

Слайд 7 20 Диагонали параллелепипеда пересекаются в одной точке и делятся

этой точкой пополам.

A
B
C
D
A1
B1
C1
D1
Рассмотрим четырехугольник A1D1CB,диагонали

которого A1C и D1B являются диагоналями параллелепипеда ABCDA1B1C1D1.Т.к. A1D1//BC и A1D1=BC,то A1D1CB- параллелограмм, поэтому диагонали A1C и D1B пересекаются в некоторой точке О и этой точкой делятся пополам.

О

20 Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. ABCDA1 B1 C1 D1

Скачать презентацию

Теги

параллелепипед

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей