Слайд 1Первичные описательные статистики
К первичным описательным статистикам (Descriptive Statistics) обычно относят
числовые характеристики распределения измеренного на выборке признака.
Каждая такая характеристика
отражает в одном числовом значении свойство распределения множества результатов измерения: с точки зрения их расположения на числовой оси либо с точки зрения их изменчивости.
Основное назначение каждой из первичных описательных статистик - замена множества значений признака, измеренного на выборке, одним числом (например, средним значением как мерой центральной тенденции).
Слайд 2Меры центральной тенденции
Мера центральной тенденции (Central Tendency) - это число,
характеризующее выборку по уровню выраженности измеренного признака.
Способы определения «центральной тенденции»:
Мода
Медиана
Выборочное
среднее
Слайд 3Меры центральной тенденции
Мода (Mode) - это такое значение из множества
измерений, которое встречается наиболее часто.
Моде, или модальному интервалу признака,
соответствует наибольший подъем (вершина) графика распределения частот. Если график распределения частот имеет одну вершину, то такое распределение называется унимодальным.
Например, в следующем массиве: {2, 3, 5, 1, 4, 5, 6, 5, 2} модой будет являться значение 5 (обозначается следующим образом: Мо = 5).
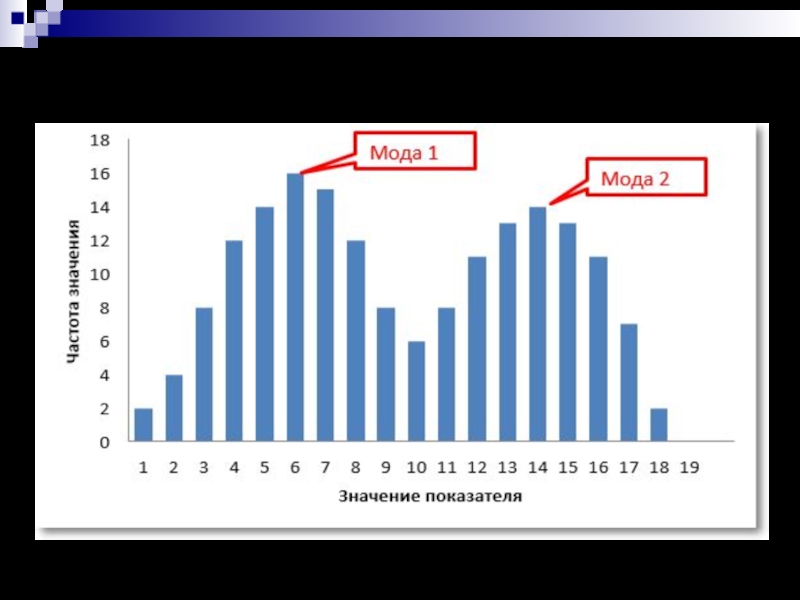
Слайд 4Если выборка содержит две моды, то распределение называется бимодальным.
Пример:
массив {3, 3, 5, 1, 4, 5, 6, 5, 3}
(Мо1 = 5, а Мо2 = 3).
Бимодальное или полимодальное (содержащее более двух мод) распределения могут рассматриваться как признак неоднородности выборки.
Например, школьный класс образован в результате механического слияния двух разных классов, и показатели мод интеллекта были изначально различны. После слияния в объединенной выборке график интеллекта будет иметь две моды.
Слайд 6Когда все значения в выборке встречаются одинаково часто принято считать
что этот выборочный ряд не имеет моды.
Например, 5 5
6 6 7 7 - в этой выборке моды нет.
Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака Эта группа называется модальной группой.
Слайд 7Для интервального ряда распределения мода определяется по формуле:
где ХMo -
нижняя граница модального интервала;
hMo - величина модального интервала;
fMo – частота
модального интервала;
fMo-1 и fMo+1 - частота интервала соответственно
предшествующего модальному и следующего за ним.
Слайд 8Например: Распределение учителей по стажу работы характеризуется следующими данными.
Определить моду
интервального ряда распределения.
Мода интервального ряда составляет
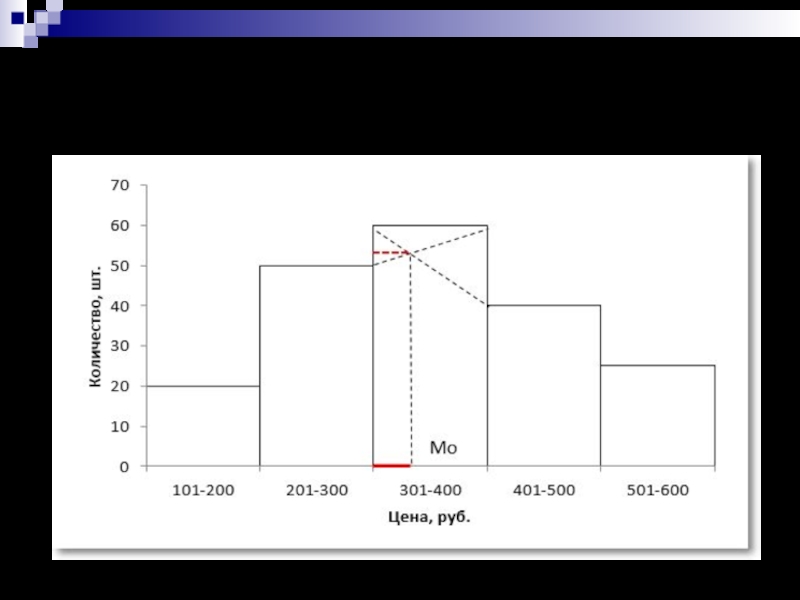
Слайд 9
Графический способ определение моды для интервального ряда (закупка учебников)
Слайд 10Меры центральной тенденции
Медиана (Median, Md или Me) - это такое
значение признака, которое делит упорядоченное (ранжированное) множество данных пополам так,
что одна половина всех значений оказывается меньше медианы, а другая - больше.
Таким образом, первым шагом при определении медианы является упорядочивание (ранжирование) всех значений по возрастанию или убыванию. Далее медиана определяется следующим образом:
если данные содержат нечетное число значений
{ 8, 9, 10, 13, 15 }, то медиана есть центральное значение, т. е. Md= 10;
если данные содержат четное число значений
{ 5, 8, 9, 11}, то медиана есть точка, лежащая посередине между двумя центральными значениями, т. е. Md =(8+9)/2 = 8,5.
Слайд 11
Чтобы определить медиану для сгруппированных данных, необходимо считать накопленные частоты.
Например:
По имеющимся данным определим медиану размера обуви воспитанников из детских
домов.
Для определения медианы надо подсчитать сумму накопленных частот ряда. Наращивание итога продолжается до получения накопленной суммы частот, превышающей половину суммы частот ряда. В нашем примере сумма частот составила 300, её половина – 150. Накопленная сумма частот получилась равной 169. Варианта, соответствующая этой сумме, т.е. 37 и есть медиана ряда.
Слайд 12Среднее (Mean) (Мх или - выборочное среднее, среднее арифметическое) -
определяется как сумма всех значений измеренного признака, деленная на количество
суммированных значений.
Если некоторый признак X измерен в группе испытуемых численностью n, мы получим значения: х1, х2, ..., xi ..., xn (где i — текущий номер испытуемого, от 1 до n). Тогда среднее значение Мх определяется по формуле:
В качестве примера можно рассмотреть массив: {8, 9, 11, 12, 12, 13, 14, 17, 19, 19, 20, 20}. Мх = (8 + 9 + 11 + 2 х 12 + 13 + 14 + 17 + 2 х 19 + 2 х 20) / 12 = 14,5
Если в ряду данных присутствуют числа со знаком «минус», то суммирование производится с учетом этих знаков.
Среднее значение весьма чувствительно к «выбросам» - экстремально малым или большим значениям переменной.
Меры центральной тенденции
Слайд 13Выбор меры центральной тенденции
Для номинативных данных единственной подходящей мерой центральной
тенденции является мода.
Для порядковых данных мера центральной тенденции мода и
медиана.
Для метрических переменных - мода, медиана и среднее.
Если распределение унимодальное и симметричное, то мода, медиана и среднее совпадают.
Чем больше отклонение от симметричности, тем больше расхождение между значениями этих мер центральной тенденции. По этому расхождению можно судить о том, насколько симметрично или асимметрично распределение.
Слайд 14Выбор меры центральной тенденции
Выборочные средние можно сравнивать, если выполняются следующие
условия:
группы достаточно большие, чтобы судить о форме распределения;
распределения симметричны;
отсутствуют «выбросы».
Если
хотя бы одно из перечисленных условий не выполняется, то следует ограничиться модой и медианой. Альтернативой является «сквозное» ранжирование представителей сравниваемых групп и сравнение средних, вычисленных для рангов этих групп.
Слайд 15Меры изменчивости
Используя для описания ряда значений признака, только меру центральной
тенденции, можно сильно ошибиться в оценке характера изучаемой совокупности.
Например,
1
группа – 10, 10, 10, 50, 50, 50
2 группа – 30, 30, 30, 30, 30, 30
Мера центральной изменчивости (Dispersion) – численное выражение величины межиндивидуальной вариации признака. Позволяет выявлять выраженность индивидуальных различий испытуемых по измеренному признаку.
Слайд 16Способы определения выраженности индивидуальных различий:
Размах
Дисперсия
Стандартное отклонение
Коэффициент вариации
Слайд 17Наиболее простой мерой изменчивости является размах, указывающий на диапазон изменчивости
значений.
Размах (Range) - это разность максимального и минимального значений
вариационного ряда:
R = xmax – xmin.
Пример: {11, 9, 12, 8, 13, 14, 17, 19, 20, 19}.
чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот.
Размах – неустойчивая мера изменчивости, на которую влияют любые возможные «выбросы».
Слайд 18Меры изменчивости
Дисперсия (S2, Dx) (Variance) - мера изменчивости для метрических
данных относительно среднего значения. Дисперсия показывает разброс значений признака относительно
своего среднего арифметического значения, то есть насколько плотно значения признака группируются вокруг Мх.
Чем больше разброс, тем сильнее варьируются результаты испытуемых в данной группе, тем больше индивидуальные различия между испытуемыми.
Выборочная дисперсия:
где xi - каждое наблюдаемое значение признака; М - среднее арифметическое значение признака; n - количество наблюдений
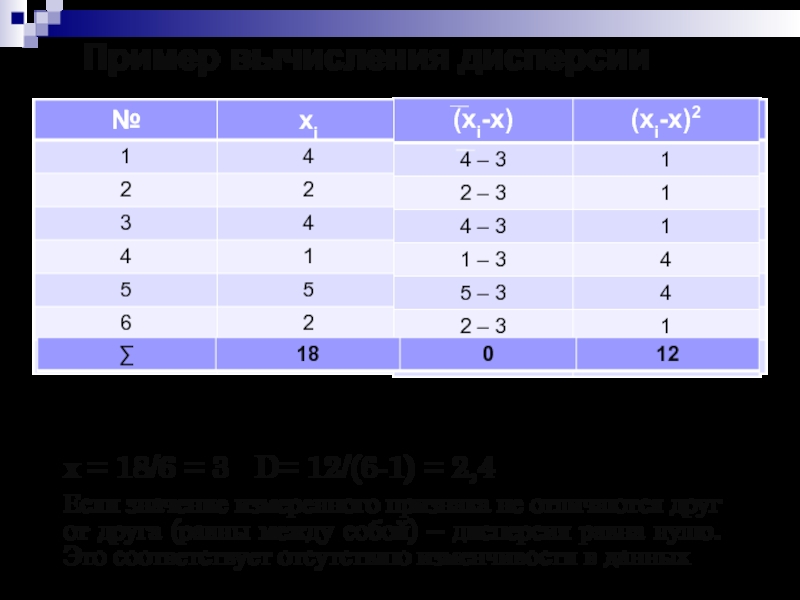
Слайд 19Пример вычисления дисперсии
х = 18/6 = 3 D= 12/(6-1)
= 2,4
Если значение измеренного признака не отличаются друг от
друга (равны между собой) – дисперсия равна нулю. Это соответствует отсутствию изменчивости в данных
Слайд 20СТАНДАРТНОЕ ОТКЛОНЕНИЕ (S,σ) - (Std. deviation) (сигма, среднеквадратическое отклонение)
Положительное значение
квадратного корня из дисперсии:
На практике чаще используется именно стандартное отклонение,
т.к. оно выражает изменчивость в исходных единицах измерения признака.
Большую наглядность в отношении разброса имеет среднеквадратическое отклонение, так как его размерность соответствует размерности измеряемой величины.
Слайд 21Из всех показателей вариации среднеквадратическое отклонение в наибольшей степени используется
для проведения других видов статистического анализа. Однако среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности значений и чтобы понять, насколько она велика относительно самих значений, требуется относительный показатель. Такой показатель называется коэффициент вариации.
Коэффициент вариации – наиболее универсальный показатель, отражающий степень разбросанности значений независимо от их масштаба и единиц измерения. Коэффициент вариации измеряется в процентах и может быть использован для сравнения вариации различных процессов и явлений.
Формула коэффициента вариации:
Слайд 22В статистике принято, что, если коэффициент вариации меньше 10%, то
степень рассеивания данных считается незначительной,
от 10% до 20% -
средней,
больше 20% и меньше или равно 33% - значительной,
значение коэффициента вариации не превышает 33%, то совокупность считается однородной,
если больше 33%, то – неоднородной.
Средние, рассчитанные для однородной совокупности – значимы, т.е. действительно характеризуют эту совокупность, для неоднородной совокупности – незначимы, не характеризуют совокупность из-за значительного разброса значений признака в совокупности.
Слайд 23Меры положения
(квантили распределения)
Квантиль – это точка на числовой оси
измеренного признака, которая делит всю совокупность упорядоченных измерений на группы
с известным соотношением их численности.
Обычно выделяют следующие разновидности квантилей:
1) Квартили Q1, Q 2, Q3 – они делят распределение на четыре части по 25% в каждой;
2) Квинтили К1, К2, К3, К4 – они делят распределение на пять частей по 20% в каждой;
3) Децили D1, ...,D9, их девять, и они делят распределение на десять частей по 10% в каждой;
4) Процентили P1, Р2 ...,Р99, девяносто девять точек, и они делят распределение на сто частей по 1% в каждой части.
Поскольку процентиль – наиболее мелкое деление, то все другие квантили могут быть представлены через процентили.
Например, первый квартиль – это двадцать пятый процентиль, первый квинтиль – второй дециль или двадцатый процентиль, и т.п.