Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка к ЕГЭ
Содержание
- 1. Подготовка к ЕГЭ
- 2. Задачи по геометрии в пробных вариантах ЕГЭ
- 3. Задание на дом:Повторить гл.3, определения и формулировки теорем.ЕГЭ 2009, вар.5,В10,В11.
- 4. Проверка домашнего задания.
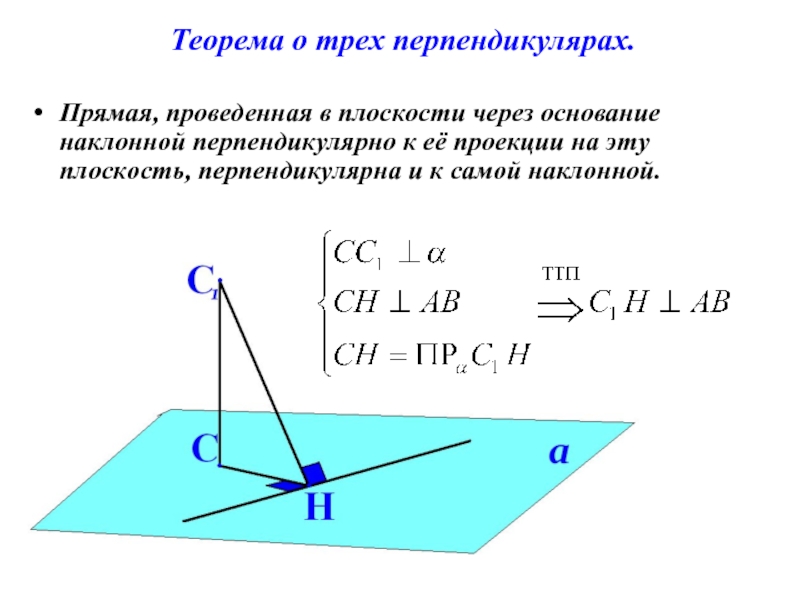
- 5. Теорема о трех перпендикулярах.Прямая, проведенная в плоскости
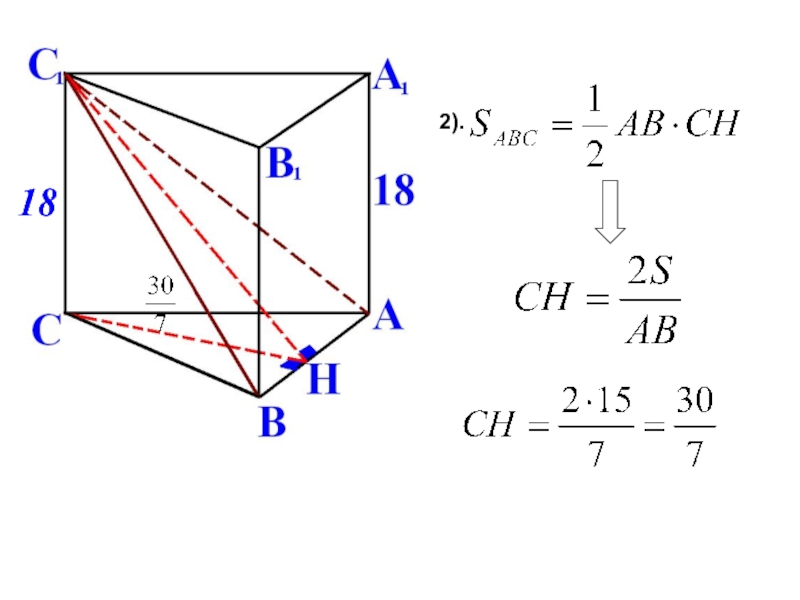
- 6. Площадь треугольникаПлощадь треугольника равна половине произведения его основания на высоту.
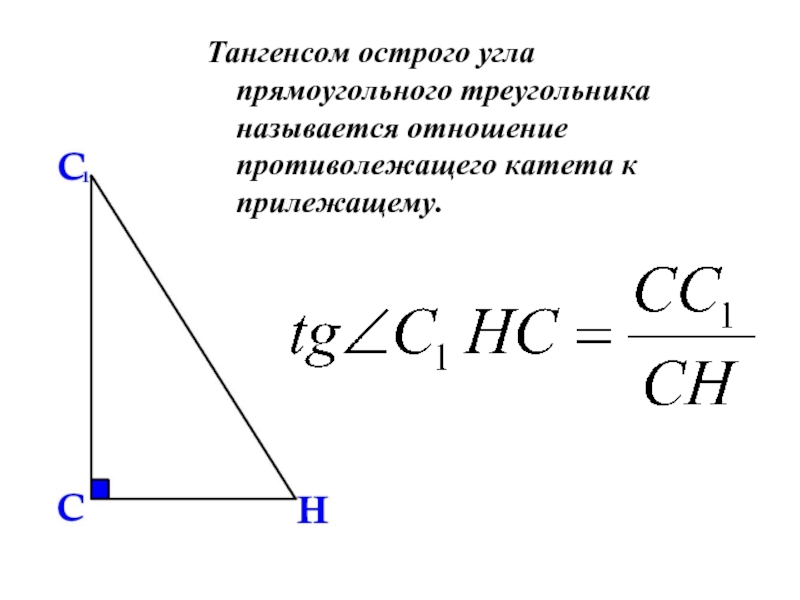
- 7. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- 8. 1).Построим
- 9. 2).18
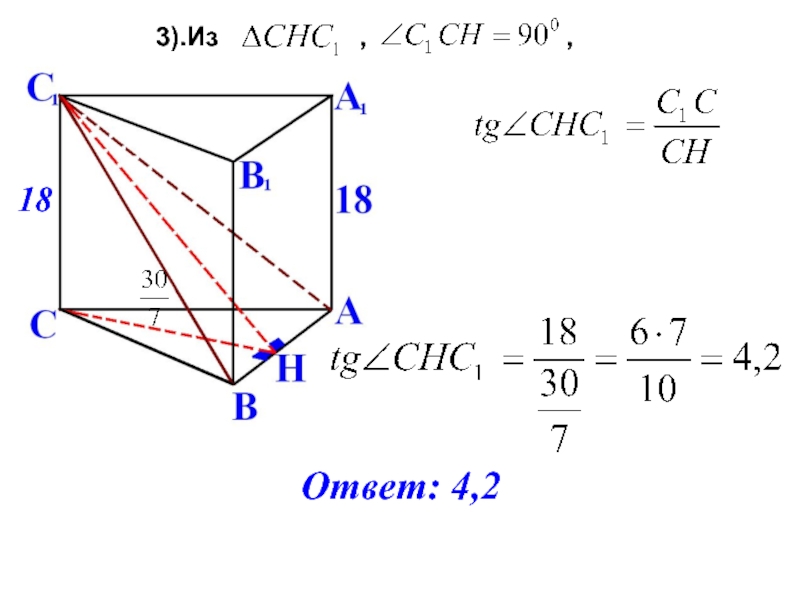
- 10. 3).Из
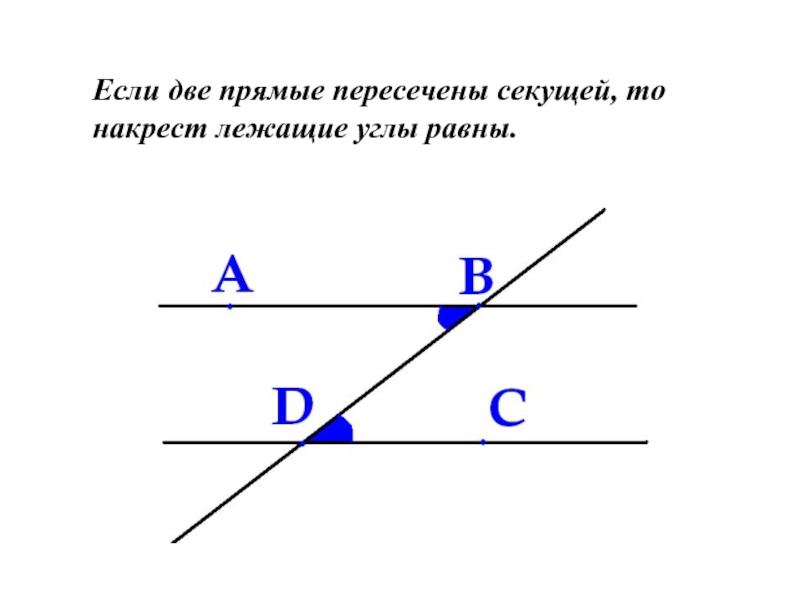
- 11. Если две прямые пересечены секущей, то накрест лежащие углы равны.
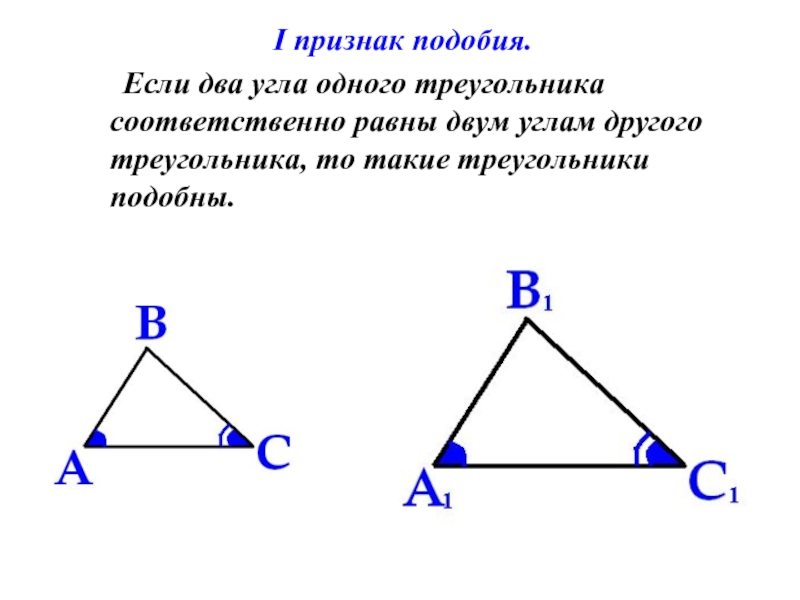
- 12. I признак подобия. Если два
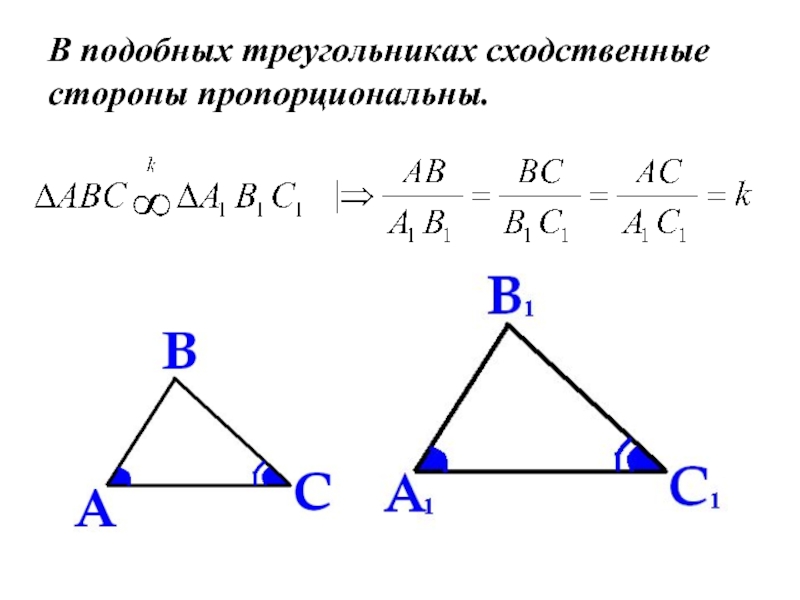
- 13. В подобных треугольниках сходственные стороны пропорциональны.
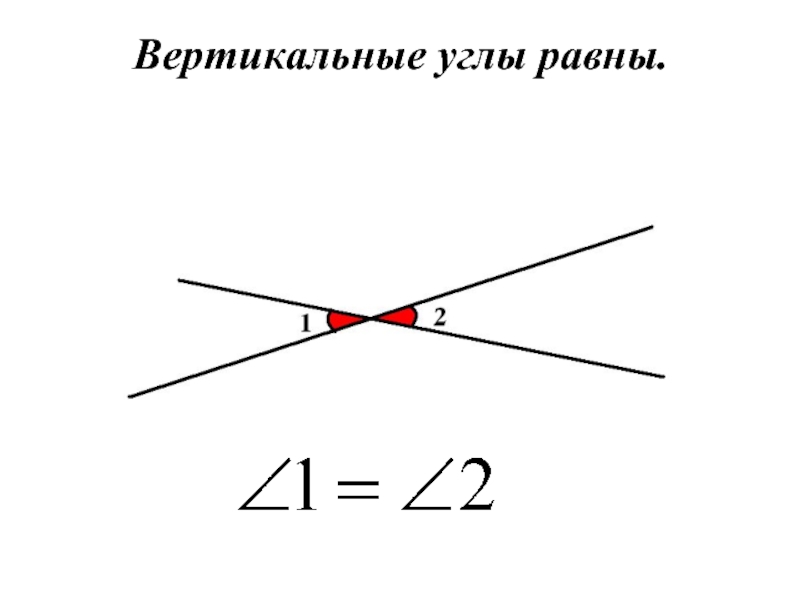
- 14. Вертикальные углы равны.
- 15. В параллелограмме АBCD биссектриса угла
- 16. 3).Из пунктов 1 и 2 следует, что
- 17. 5).
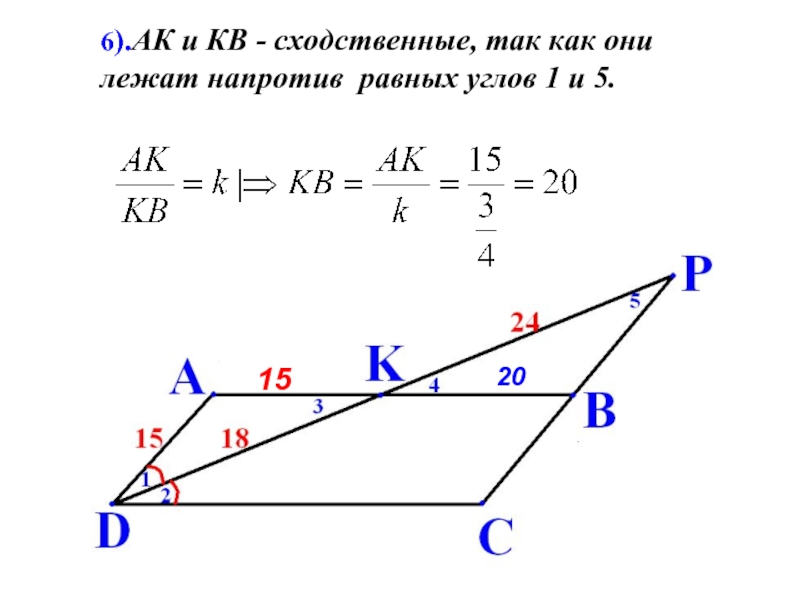
- 18. 6).АК и КВ - сходственные, так как они лежат напротив равных углов 1 и 5.2015
- 19. 9).
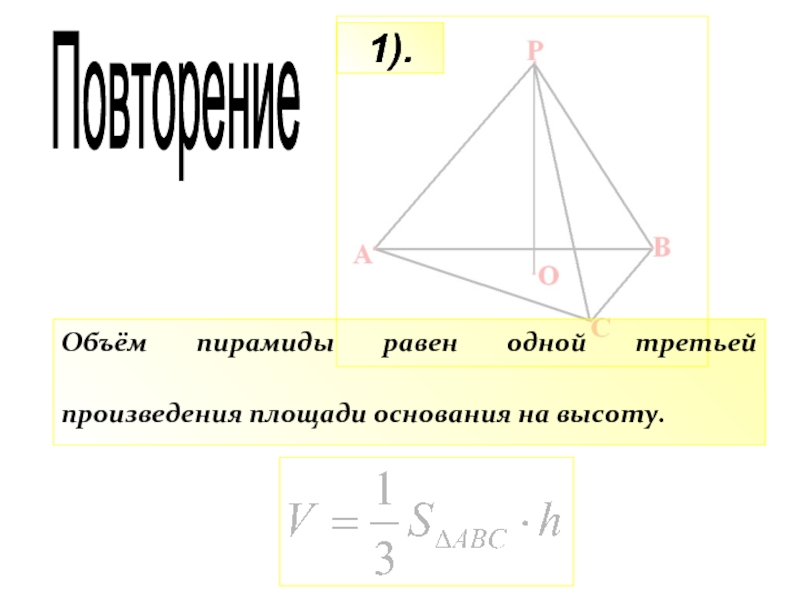
- 20. 1).Объём пирамиды равен одной третьей произведения площади основания на высоту. Повторение
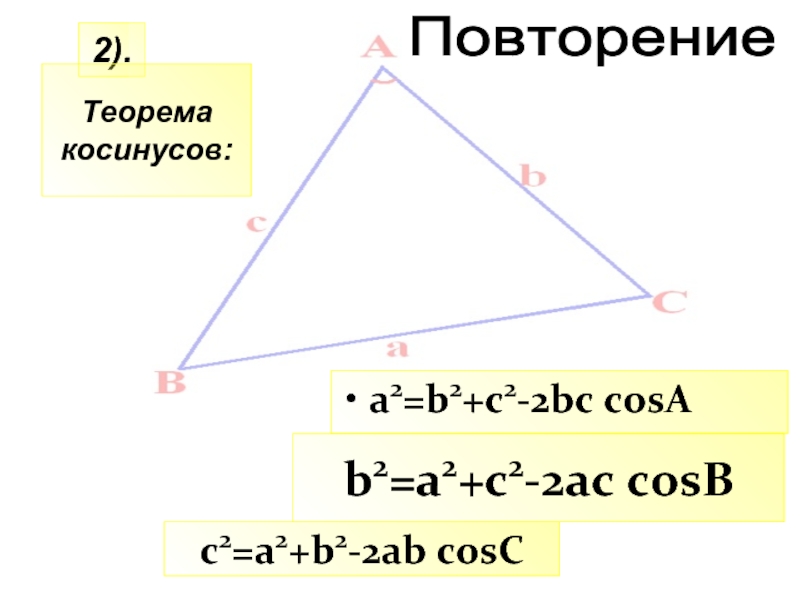
- 21. c2=a2+b2-2ab cosC2).b2=a2+c2-2ac cosBПовторениеa2=b2+c2-2bc cosAТеорема косинусов:
- 22. Теорема Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».c2=a2+b23).Повторение
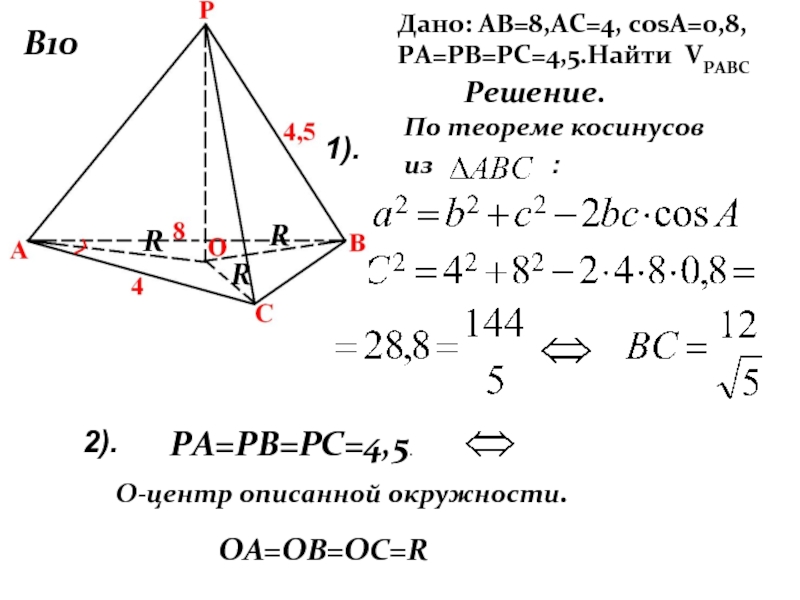
- 23. В10Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС Решение.По теореме
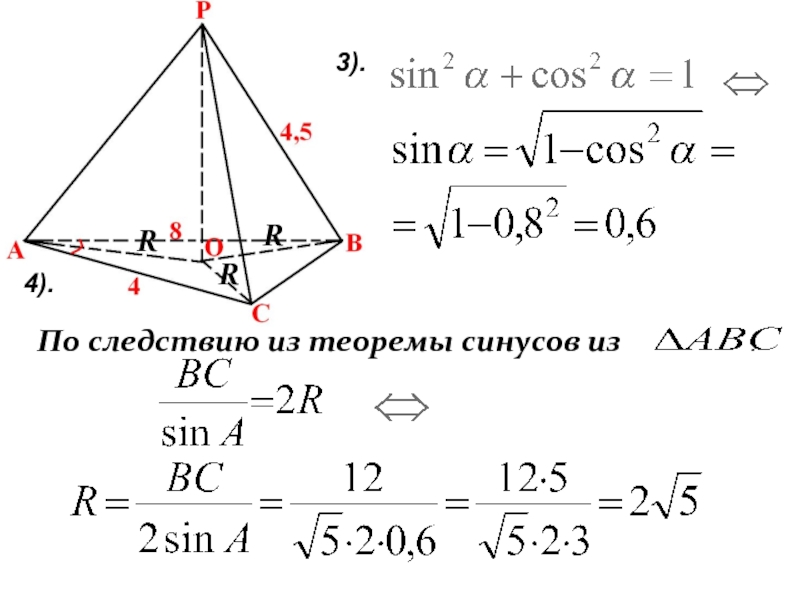
- 24. 4).По следствию из теоремы синусов из
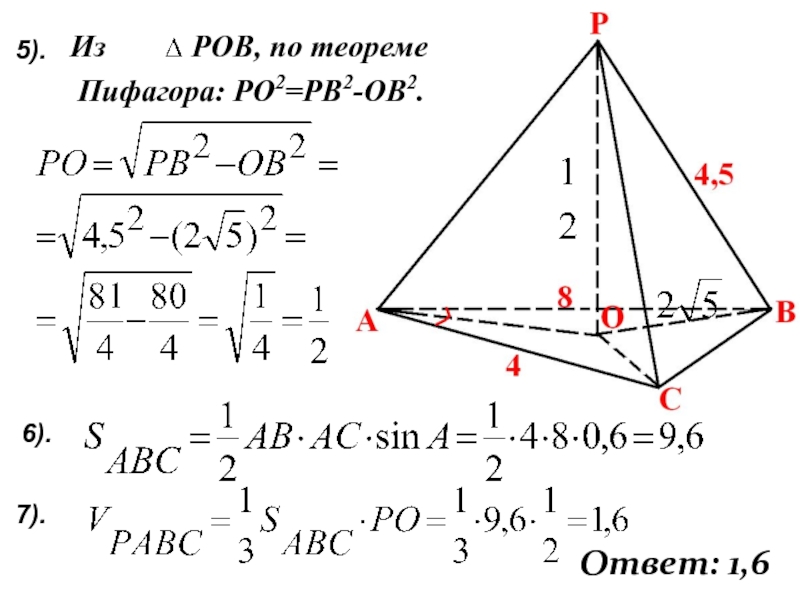
- 25. Из РОВ, по теореме Пифагора: РО2=РВ2-ОВ2.7).Ответ: 1,65).6).
- 26. Самостоятельная работа.I вар. Основание прямой призмы
- 27. Скачать презентанцию
Слайды и текст этой презентации
Слайд 6Площадь треугольника
Площадь треугольника равна половине произведения его основания на высоту.
Слайд 7Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к
прилежащему.
Слайд 81).Построим
и С1Н.Так как призма прямая, то её боковые ребра перпендикулярны
основанию. Основание прямой призмы АВСА1В1С1-треугольник АВС, площадь которого равна 15, АВ=7. Боковое ребро призмы равно 18. Найдите тангенс угла между плоскостью основания призмы и плоскостью АВС1.
В 10
Решение
-линейный угол двугранного угла САВС1 ,так как его стороны перпендикулярны ребру угла САВС1.
Слайд 12I признак подобия.
Если два угла одного треугольника
соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Слайд 15 В параллелограмме АBCD биссектриса угла D пересекает сторону AD
в точке К и прямую ВС в точке Р. Найдите
периметр треугольника СDР, если DК=18, РК=24, АD=15.В10.
Слайд 163).Из пунктов 1 и 2 следует, что
,
а значит AD=AK=15, так как напротив равных углов лежат равные стороны.1).Углы 2 и 3 равны, как накрест лежащие при AB||DC и секущей DP
15
2).Углы 1 и 2 равны, так как DК- биссектриса.
Слайд 175).
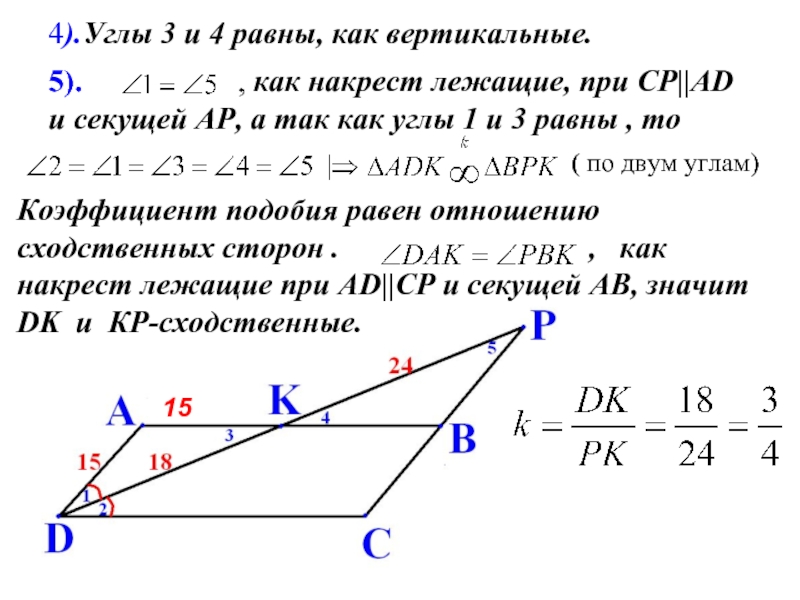
, как накрест лежащие, при СР||AD и секущей АР,
а так как углы 1 и 3 равны , то( по двум углам)
4).Углы 3 и 4 равны, как вертикальные.
Коэффициент подобия равен отношению сходственных сторон . , как накрест лежащие при AD||CP и секущей АВ, значит DK и КP-сходственные.
15
Слайд 199).
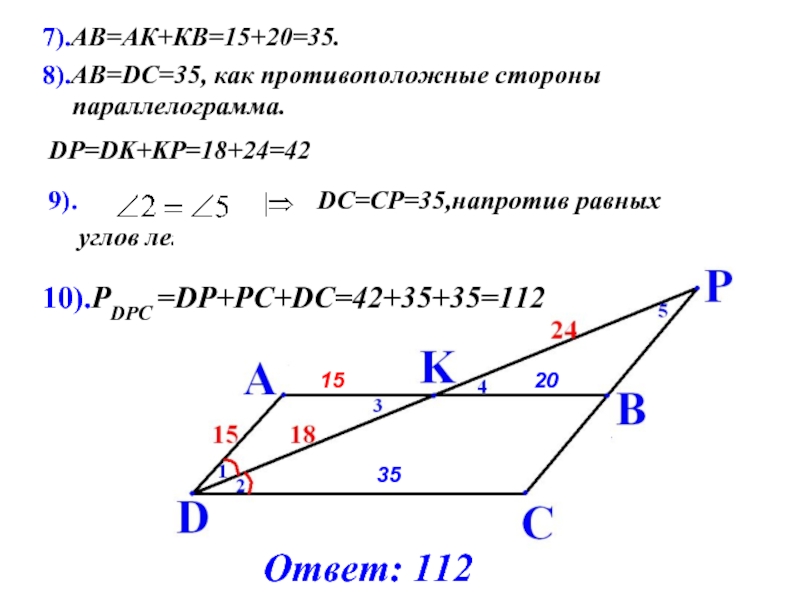
DC=CP=35,напротив равных
углов лежат равные стороны.15
20
DP=DK+KP=18+24=42
8).АВ=DС=35, как противоположные стороны параллелограмма.
35
10).РDPC =DP+PC+DC=42+35+35=112
7).АВ=АК+КВ=15+20=35.
Ответ: 112
Слайд 22Теорема Пифагора:
«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
c2=a2+b2
3).
Повторение
Слайд 23В10
Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС
Решение.
По теореме косинусов
из
:
2).
1).
РА=РВ=РС=4,5.
OА=OВ=OС=R
O-центр описанной окружности.
R
R
R
Слайд 26Самостоятельная
работа.
I вар. Основание прямой призмы АВСА1В1С1-треугольник АВС, площадь которого
равна 15, ВС=7. Боковое ребро призмы равно 12. Найдите тангенс
угла между плоскостью основания призмы и плоскостью ВСА1.II вар. Основание прямой призмы АВСА1В1С1-треугольник АВС, площадь которого равна 15, АС=7. Боковое ребро призмы равно 24. Найдите тангенс угла между плоскостью основания призмы и плоскостью АСВ1.