Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Программирование 1
Содержание
- 1. Программирование 1
- 2. 13.10.2011Вычисления с вещественными числами 2Вычисления с вещественными числами и машинное эпсилон
- 3. 13.10.2011Вычисления с вещественными числами 2Вычисления с вещественными числами и машинное эпсилон
- 4. 13.10.2011Вычисления с вещественными числами 2Особенности системы F (t, L, U)
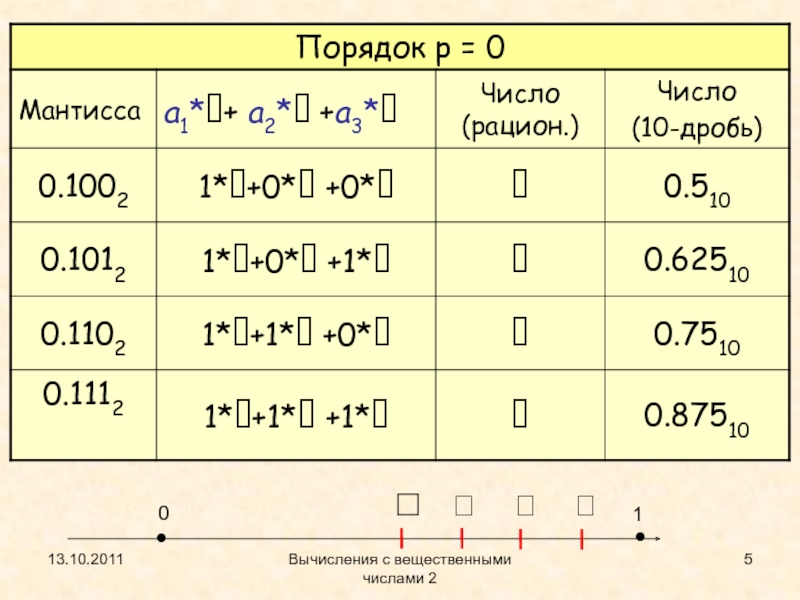
- 5. 13.10.2011Вычисления с вещественными числами 210
- 6. 13.10.2011Вычисления с вещественными числами 2012111
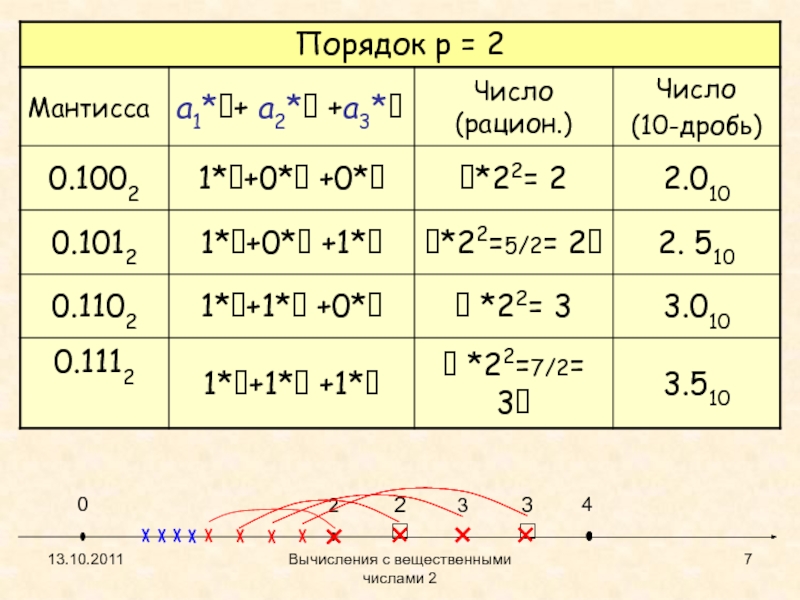
- 7. 13.10.2011Вычисления с вещественными числами 22
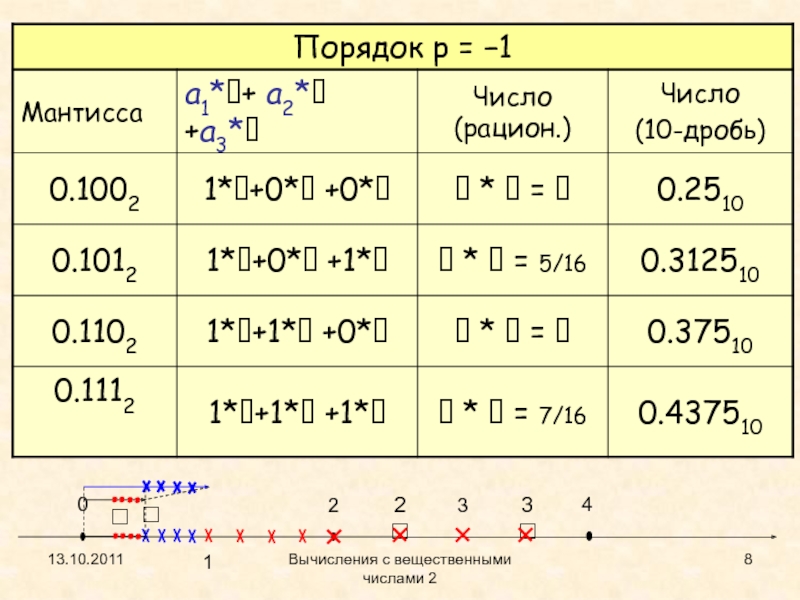
- 8. 13.10.2011Вычисления с вещественными числами 20423321
- 9. 13.10.2011Вычисления с вещественными числами 2Особенности
- 10. 13.10.2011Вычисления с вещественными числами 2
- 11. 13.10.2011Вычисления с вещественными числами 2Особенности вычислений с
- 12. 13.10.2011Вычисления с вещественными числами 25/16 + 2
- 13. Стандарт 754 (IEEE) – 1985 г. –
- 14. 13.10.2011Вычисления с вещественными числами 2Стандартные формы чисел
- 15. 13.10.2011Вычисления с вещественными числами 2Формат чисел типов
- 16. 13.10.2011Вычисления с вещественными числами 2Машинное эпсилонВ качестве
- 17. Встроенное в программу («эмпирическое») вычисление машинного эпсилонtypedef
- 18. Встроенное в программу («эмпирическое») вычисление машинного эпсилон
- 19. 13.10.2011Вычисления с вещественными числами 2Рекомендации программистуПамять более
- 20. Полезное отступлениеВывод результатов работы программы в файл
- 21. Рекомендации книг по C++См. файл «книги С++.ppt»13.10.2011Вычисления с вещественными числами 2
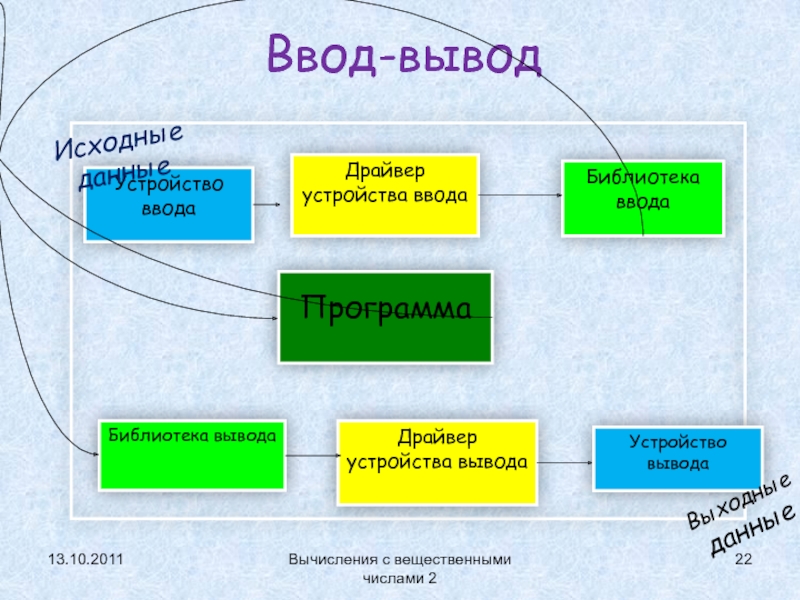
- 22. Ввод-вывод13.10.2011Вычисления с вещественными числами 2
- 23. Модель потока выводаПоток (типа) ostreamПреобразует значения разных
- 24. c(1,234)123“откуда-то”Вычисления с вещественными числами 2bufferistreamМодель потока вводаЗначения
- 25. Нами уже использовалисьСтандартные потоки (из библиотеки iostream):
- 26. Файлы. Обобщенная модель ДискСистема ввода-выводаОсновная памятьФайлы(последовательности байтов)Потоки
- 27. Имя потока вывода#include // подключить библиотеку13.10.2011Вычисления с
- 28. Демонстрация программ про машинное ЭПСИЛОН Программы про
- 29. Конец отступления про вывод в файл13.10.2011Вычисления с вещественными числами 2
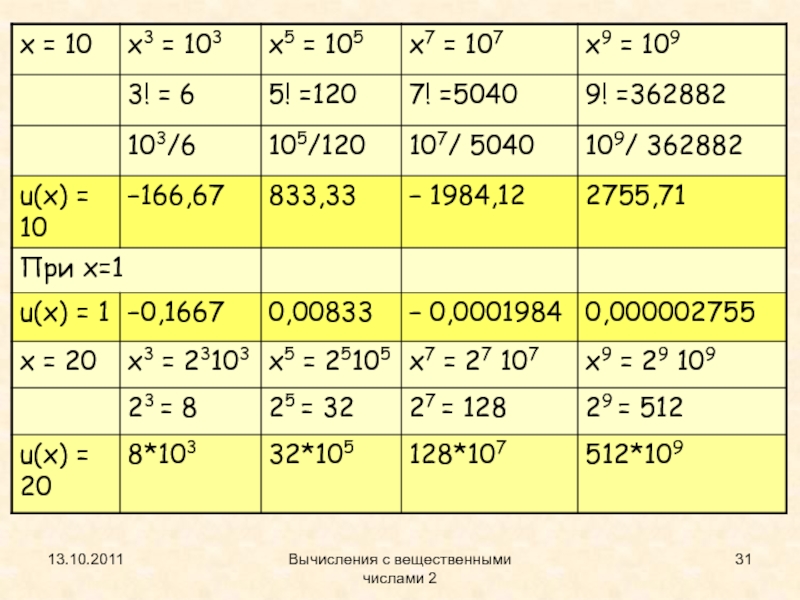
- 30. 13.10.2011Вычисления с вещественными числами 2Анализ примера с
- 31. 13.10.2011Вычисления с вещественными числами 2
- 32. 13.10.2011Вычисления с вещественными числами 2Машинное эпсилон и
- 33. 13.10.2011Вычисления с вещественными числами 2Пример. Проверка ортогональности
- 34. 13.10.2011Вычисления с вещественными числами 2 вектор нормали прямой ортогональность прямыхОтложено
- 35. 13.10.2011Вычисления с вещественными числами 2КОНЕЦ ЛЕКЦИИКОНЕЦ
- 36. Скачать презентанцию
13.10.2011Вычисления с вещественными числами 2Вычисления с вещественными числами и машинное эпсилон
Слайды и текст этой презентации
Слайд 113.10.2011
Вычисления с вещественными числами 2
Программирование 1
Лекция 7
Вычисления с вещественными числами
(продолжение):
Слайд 213.10.2011
Вычисления с вещественными числами 2
Вычисления с вещественными числами и машинное
эпсилон
Слайд 313.10.2011
Вычисления с вещественными числами 2
Вычисления с вещественными числами и машинное
эпсилон
Слайд 1113.10.2011
Вычисления с вещественными числами 2
Особенности вычислений с вещественными числами. Дополнение.
Нарушение ассоциативности сложения:
(a + b) + c a
+ (b + c) Пример:
5/16 + (2 1) (5/16 + 2) 1
5/16 + (2 1) = 5/16 + 1= 0.101*21 + 0.100*21 =
= (0.101*22 + 0.100*20) * 21=
= (0.00101*20 + 0.100*20) * 21=
= (0.001[01] + 0.100) * 21= (0.101[01]) * 21=
= 0.101* 21 = 5/4 = 1.
Точный результат = 21/16 = 1+5/16
Следствие: результат зависит от порядка суммирования
Слайд 1213.10.2011
Вычисления с вещественными числами 2
5/16 + 2 = 0.101*21 +
0.100*22 =
= (0.101*23 + 0.100*20) * 22=
= (0.000101*20 +
0.100*20) * 22== (0.000[101] + 0.100) * 22= (0.100[101]) * 22 =
0.100* 22 = 2 в режиме «отбрасывания»
=
0.101* 22 = 2 в режиме округления
1 в режиме «отбрасывания»
(5/16 + 2) 1 =
1 в режиме округления
Т.о. 1 1 и 1 1
1
1
1
1+5/16
Слайд 13Стандарт 754 (IEEE) – 1985 г. – «плавающая точка IEEE»
формат
одинарной точности (в B-Pascal – тип single, в С/С++ -
float);формат двойной точности (в BP и в – тип С/С++ double);
формат расширенной (повышенной) точности (в BP – тип Extended ). (long double ?)
13.10.2011
Вычисления с вещественными числами 2
Стандартные формы чисел с плавающей точкой:
Слайд 1413.10.2011
Вычисления с вещественными числами 2
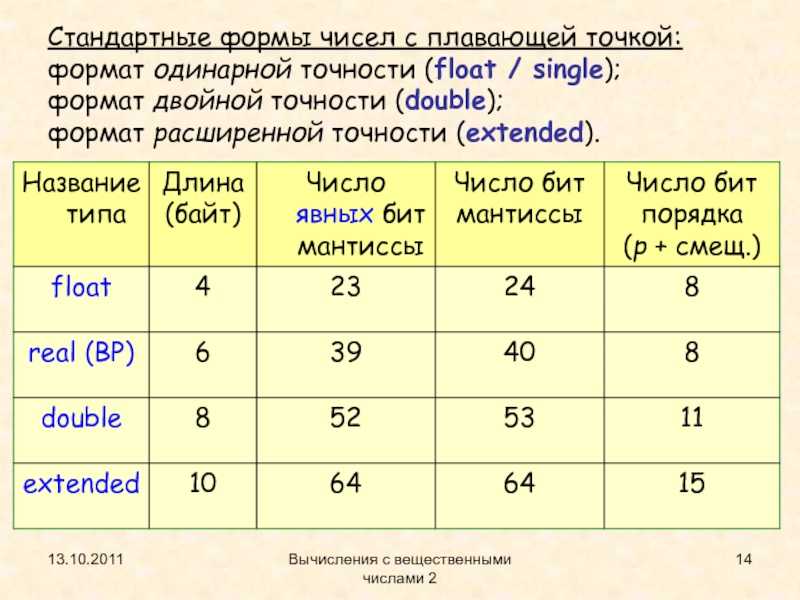
Стандартные формы чисел с плавающей точкой:
формат
одинарной точности (float / single); формат двойной точности (double); формат расширенной точности
(extended).
Слайд 1513.10.2011
Вычисления с вещественными числами 2
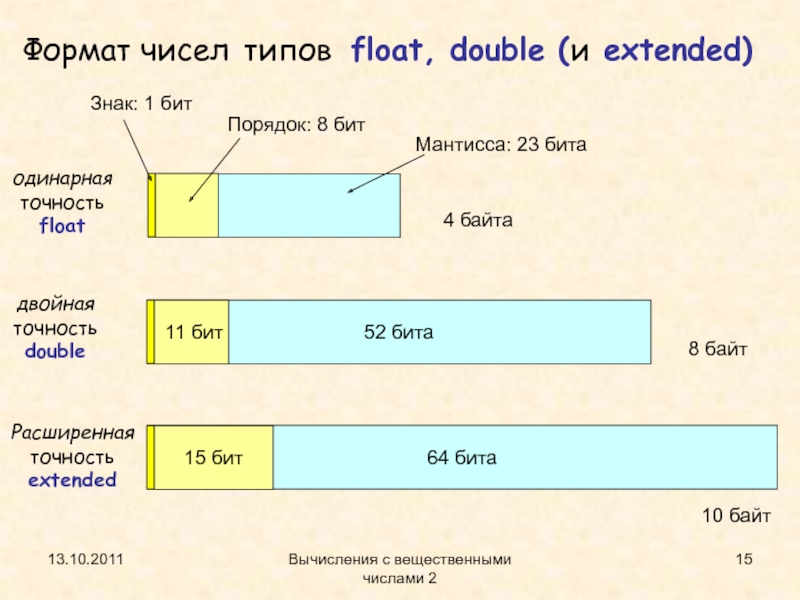
Формат чисел типов float, double (и
extended)
одинарная точность float
двойная точностьdouble
Расширенная точность extended
Знак: 1 бит
Порядок: 8
битМантисса: 23 бита
4 байта
8 байт
10 байт
Слайд 1613.10.2011
Вычисления с вещественными числами 2
Машинное эпсилон
В качестве характеристики точности
представления
вещественных чисел в ЭВМ
используют так называемое машинное эпсилон,
определяемое
как eps = min { >0: fl ( + 1) > 1 }.
Эта величина учитывает особенности реализации
системы F(t, L, U) в конкретном типе компьютера.
Проблема переносимости ПО (библиотек).
1
0.10…001*21
eps
пусто
Слайд 17Встроенное в программу («эмпирическое») вычисление машинного эпсилон
typedef float real;
// (long) double
real eps, epsP1, epsil;
int i;
i = 0;
eps = 1.0; epsP1 = 2.0;while (epsP1 > 1.0) { // eps=2^(-i) && (1+eps>1)
eps = eps * 0.5;
epsP1 = eps + 1.0;
i = i + 1;
} //end: eps=2^(-i) && !(1+eps>1) && (1+2*eps>1)
epsil = 2.0 * eps;
13.10.2011
Вычисления с вещественными числами 2
eps1.cpp
Слайд 18Встроенное в программу («эмпирическое») вычисление машинного эпсилон (найди отличия!)
typedef
float real; // (long) double
real eps, epsil;
int i;
i =
0; eps = 1.0; while (eps+1.0 > 1.0) { // eps=2^(-i) && (1+eps>1)
eps = eps * 0.5;
i = i + 1;
} //end: eps=2^(-i) && !(1+eps>1) && (1+2*eps>1)
epsil = 2.0 * eps;
13.10.2011
Вычисления с вещественными числами 2
eps2.cpp
Анализ выполнения (eps1.cpp b, eps2.cpp) и интерпретация результатов
Слайд 1913.10.2011
Вычисления с вещественными числами 2
Рекомендации программисту
Память более важна, чем точность
одинарная точность float (single)
Точность более важна, чем память
двойная точность double (long double)[Расширенная точность Extended только в специальных случаях (с самостоятельным контролем точности программистом) – в С++ не актуально]
Слайд 20Полезное отступление
Вывод результатов работы программы в файл
Что дает?
Возможность документировать
(сохранить) для дальнейшего анализа, отчетности и т.п.
Возможность анализировать с большим
полем обзора, чем окно консоли (+ масштабирование)Возможность редактировать (модифицировать, вырезать, использовать в других документах – например, в лекциях - и т.п.)
Возможность обрабатывать другими программами (например, Exel – таблицы, графики, диаграммы и т.п.)
13.10.2011
Вычисления с вещественными числами 2
Слайд 21Рекомендации книг по C++
См. файл «книги С++.ppt»
13.10.2011
Вычисления с вещественными числами
Слайд 23Модель потока вывода
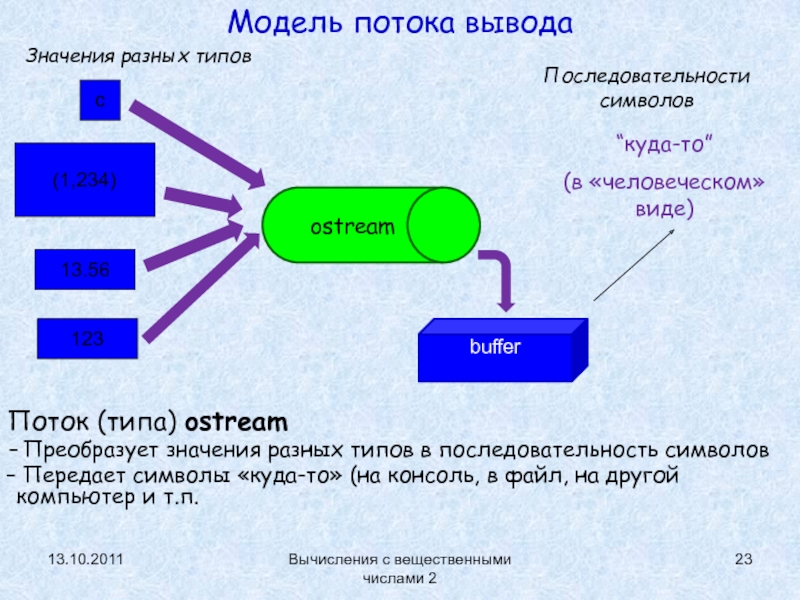
Поток (типа) ostream
Преобразует значения разных типов в последовательность
символов
Передает символы «куда-то» (на консоль, в файл, на другой
компьютер и т.п.c
(1,234)
123
“куда-то”
(в «человеческом» виде)
Вычисления с вещественными числами 2
buffer
ostream
Значения разных типов
Последовательности символов
13.56
13.10.2011
Слайд 24c
(1,234)
123
“откуда-то”
Вычисления с вещественными числами 2
buffer
istream
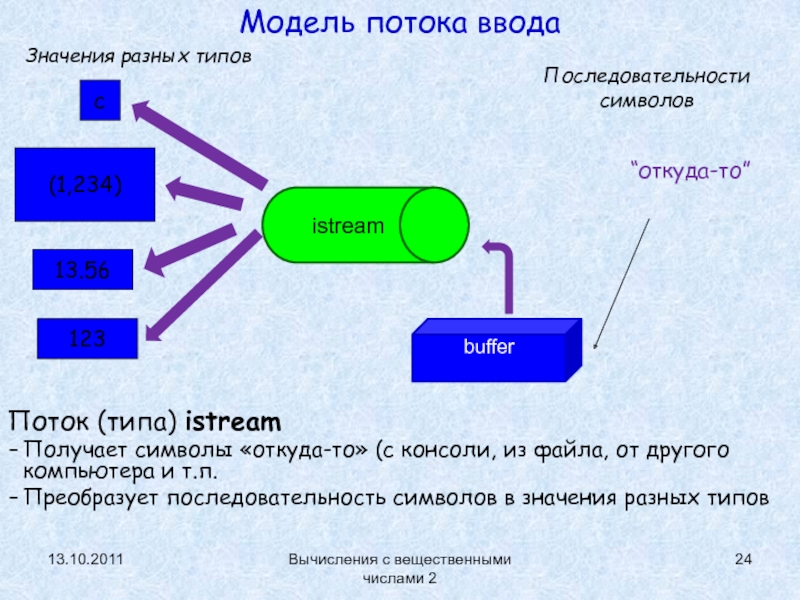
Модель потока ввода
Значения разных типов
Последовательности символов
13.56
Поток
(типа) istream
Получает символы «откуда-то» (с консоли, из файла, от другого
компьютера и т.п.Преобразует последовательность символов в значения разных типов
13.10.2011
Слайд 25Нами уже использовались
Стандартные потоки (из библиотеки iostream):
для ввода –
поток cin (типа istream)
для вывода – поток cout
(типа ostream) Подключение в программе:
#include
Для форматирования:
#include
13.10.2011
Вычисления с вещественными числами 2
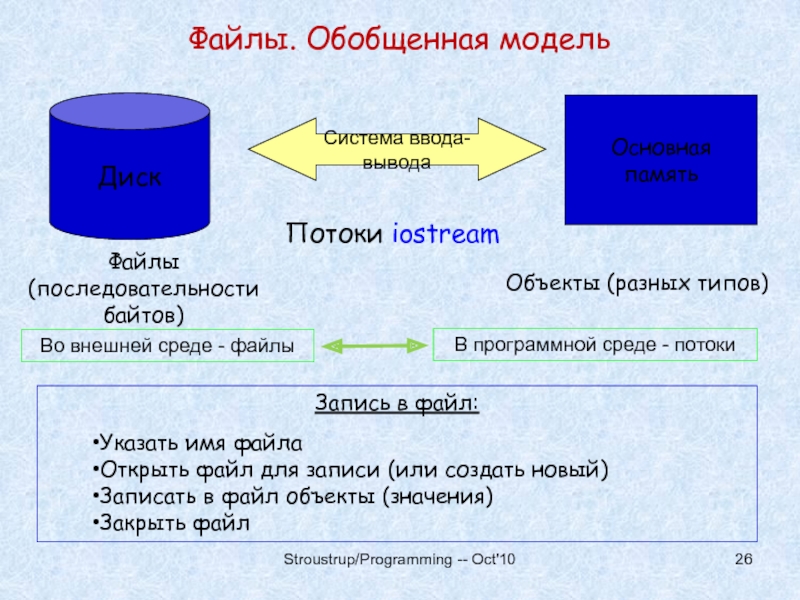
Слайд 26Файлы. Обобщенная модель
Диск
Система ввода-вывода
Основная память
Файлы
(последовательности байтов)
Потоки iostream
Объекты (разных типов)
Stroustrup/Programming
-- Oct'10
Запись в файл:
Указать имя файла
Открыть файл для записи (или
создать новый)Записать в файл объекты (значения)
Закрыть файл
Во внешней среде - файлы
В программной среде - потоки
Слайд 27Имя потока вывода
#include // подключить библиотеку
13.10.2011
Вычисления с вещественными числами
2
// открыть файл для записи с именем outputD.txt:
ofstream outfile (
"outputD.txt" );…
// запись в файл порции данных:
outfile << '<‘ << i << "> eps : " << eps << " 1 + eps :" << epsP1 << endl;
…
outfile.close(); // закрыть файл
Имя файла
См. программу eps3file.cpp – c выводом в файл для типа float
Слайд 28Демонстрация программ про машинное ЭПСИЛОН
Программы про машинное эпсилон см.
в таком порядке:
eps1.cpp – без вывода в файл
eps2.cpp – без
вывода в файл + некорректность float==doubleeps3file.cpp – c выводом в файл для float
eps3d_file.cpp – c выводом в файл для double
eps3f_file_err.cpp – c выводом в файл для float + некорректность float==double
13.10.2011
Вычисления с вещественными числами 2
Слайд 3013.10.2011
Вычисления с вещественными числами 2
Анализ примера с вычислением sin x
С
выводом в файл! См. sin3f_fil.cpp
Слайд 3213.10.2011
Вычисления с вещественными числами 2
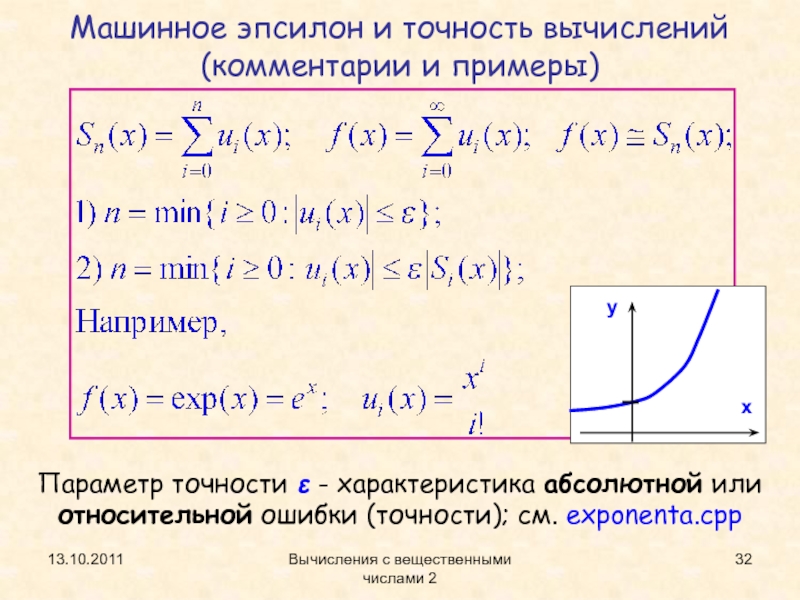
Машинное эпсилон и точность вычислений
(комментарии и
примеры)
Параметр точности - характеристика абсолютной или относительной ошибки (точности);
см. exponenta.cpp
Слайд 3313.10.2011
Вычисления с вещественными числами 2
Пример. Проверка ортогональности прямых
Изменение масштаба :
*
*> или *> *<
Отложено
Слайд 3413.10.2011
Вычисления с вещественными числами 2
вектор нормали прямой
ортогональность прямых
Отложено
Слайд 3513.10.2011
Вычисления с вещественными числами 2
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ
ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ ЛЕКЦИИ
КОНЕЦ
ЛЕКЦИИ
