Решение логарифмических
уравнений
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение логарифмических уравнений
Содержание
- 1. Решение логарифмических уравнений
- 2. 1) Уравнения вида loga x = b.
- 3. 2) Уравнения вида log a f(x) =
- 4. 3) Уравнения вида log a f (x)
- 5. 4) Уравнения вида log a f (x)
- 6. 4) Уравнения вида log a f (x)
- 7. 5) Уравнения вида log a(x) f (x)
- 8. 6) Уравнения вида log a (log b
- 9. 7) Замена переменной. Пример. lg2
- 10. 8) Приведение к одному основанию. Пример.
- 11. 9) Уравнения с неизвестным в основании логарифма.
- 12. 10) Уравнения вида logaf (x)∙logbg(x) = 0.
- 13. 11) Разложение на множители левой части уравнения.
- 14. 12) Использование формулы перехода к новому основанию.Пример.log3
- 15. 13) Использование формулы log a
- 16. 14) Использование формулы log a b
- 17. 15)Уравнения вида A∙( log a f
- 18. 16) Показательно - логарифмические уравнения. Если в
- 19. 17)Использование однородности. Уравнения вида a∙A2(х)+ b∙A(х)B(х) +
- 20. 18) Уравнения вида a loga f(x) =
- 21. 19) Уравнения вида a logс f(x) =
- 22. 20) Уравнения вида a(x) loga(x) f(x) =
- 23. 21) Использование формул loga(b/c) = log
- 24. 22) Использование формулы log f(x) (g(x))n
- 25. 23) Рационально – логарифмические уравнения. Пример.
- 26. 24) Иррационально – логарифмические уравнения. 1 случайПример.
- 27. 24) Иррационально – логарифмические уравнения. 2 случайПример
- 28. 25) Уравнения, содержащие модуль. 1случай Пример.
- 29. 25) Уравнения, содержащие модуль. 2 случайПример .
- 30. 25) Уравнения, содержащие модуль. 3 случайПример.
- 31. 26) Комбинированные уравнения.Пример 1.
- 32. 26) Комбинированные уравнения.Пример 2.
- 33. 26) Комбинированные уравнения.Пример 3. log
- 34. 27) Оценочная «граничная» задача. Производится оценка множеств
- 35. 28) Использование монотонности функций. Пример. log7(x +
- 36. Литература: 1) Алгебра. ЕГЭ:
- 37. Скачать презентанцию
1) Уравнения вида loga x = b. Уравнение вида log a x = b при всех допустимых a имеют единственное решение x = a b.Пример. log3 x = 4.
Слайды и текст этой презентации
Слайд 21) Уравнения вида loga x = b.
Уравнение вида log a
x = b при всех допустимых a имеют единственное решение
x = a b.Пример. log3 x = 4.
х = 34,
х = 81.
Ответ. х = 81.
Слайд 32) Уравнения вида log a f(x) = b.
Уравнение вида log
a f(x)= b равносильно уравнению f(x) = a b.
Пример. log2(5
– x) = 3.5 – х = 23,
х = - 3.
Ответ. х = - 3.
Слайд 43) Уравнения вида log a f (x) = g(x).
Уравнение вида
log a f (x) = g(x) равносильно уравнению f(x) =
a g(x).Пример. lg (2x + x + 4) = x – x lg5.
2x + x + 4 = 10 x-x lg 5,
2x + x + 4 = , 2x + x + 4 = ,
2x + x + 4 = ,
2x + x + 4 = 2x,
x = - 4.
Ответ. х = - 4.
Слайд 54) Уравнения вида log a f (x) = log a
g (x).
1способ решения
Уравнение вида log a f (x) = log
a g (x) равносильно системе:Причем любую из двух последних строк можно (и, как правило, нужно) опустить.
Пример. log2 (x2 + x - 2) = log2 2x.
x = 2.
Ответ. x = 2.
Слайд 64) Уравнения вида log a f (x) = log a
g (x).
2способ решения.
Решив уравнение f(x) =g(x),сделать проверку найденных корней
для исходного уравнения.Пример.log2(5x + 3) = log2(7x + 5)
5x + 3 = 7x + 5,
- 2x = 2, x = - 1.
Проверка. x = - 1.
Число x = -1 не является корнем исходного уравнения, так как при x = -1 левая и правая части уравнения теряют смысл.
Ответ. Корней нет.
Слайд 75) Уравнения вида log a(x) f (x) = log a(x)
g (x).
Уравнение вида log a(x) f(x) = log a(x) g(x)
равносильно системе: или
Пример. log 4 - x (x2 + 1) = log 4 - x (3x + 1).
x = 0.
Ответ. x1 = 0.
Слайд 86) Уравнения вида log a (log b f (x)) =
c.
При решении уравнений вида log a (log b f (x))
= c вначале потенцируют по внешнему логарифму, затем по внутреннему.Пример. log (log3x) = 4.
log2(log3x) = 2 или log 2(log3x) = - 2.
1) log2(log3x) = 2; log3x = 4; x = 81.
2) log2(log3x) = - 2; log3x = ; x = .
Ответ. x1 = 81, x2 = .
Слайд 97) Замена переменной.
Пример. lg2 + lg x
= 7.
(lg 10 – lg x)2 + lg x =
7,(1 – lg x)2 + lg x = 7.
Пусть lg x = у, тогда (1 – у)2 + у = 7,
1- 2у + у2 + у – 7 = 0,
у2 – у – 6 = 0,
у1 = 3, у2 = - 2.
Возвращаясь к переменной х, рассмотрим два случая:
1) lg x = 3, x = 103, x1 = 1000.
2) lg x = -2, x = 10-2, x2 = 0,01.
Ответ. x1 = 1000, x2 = 0,01.
Слайд 108) Приведение к одному основанию.
Пример.
= 2 – 2 .
= - ,
Решим уравнение18x2 + 18x – 1= 0.
х1,2 = = = = ,
Условию удовлетворяет х = .
Ответ. х = .
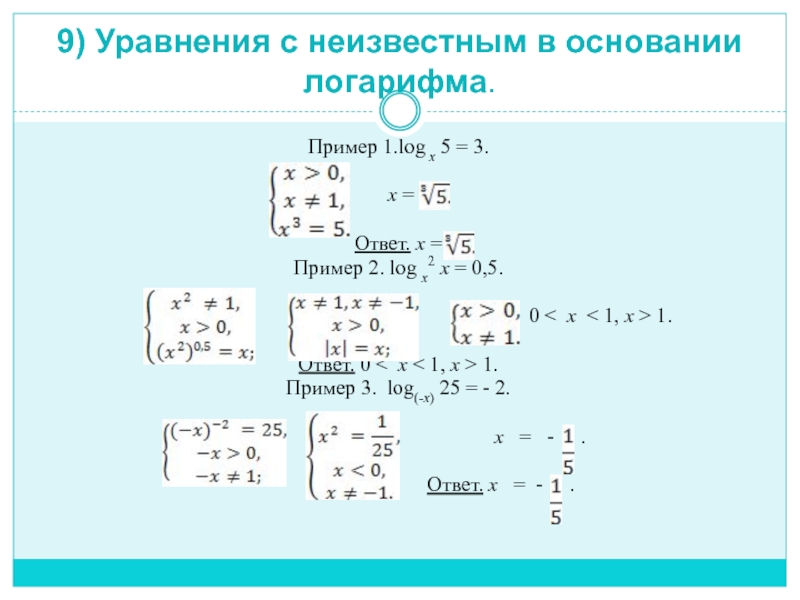
Слайд 119) Уравнения с неизвестным в основании логарифма.
Пример 1.log x 5
= 3.
x =
Ответ. x =
Пример 2.
log x2 x = 0,5.0 < x < 1, x > 1.
Ответ. 0 < x < 1, x > 1.
Пример 3. log(-x) 25 = - 2.
x = - .
Ответ. x = - .
Слайд 12 10) Уравнения вида logaf (x)∙logbg(x) = 0.
Уравнения вида log a
f(x)∙ log b g(x) = 0 равносильно системе:
Пример. log2x
∙log7(3 – x) = 0.x1 = 1, x2 = 2.
Ответ. x1 = 1, x2 = 2.
Слайд 1311) Разложение на множители левой части уравнения.
Пример. log4 (2x
– 1)∙log4x = 2 log4(2x – 1).
log4 (2x – 1)
∙ log4x - 2 log 4(2x – 1) = 0,log4 (2x – 1) ∙ (log 4 x – 2) = 0,
log4 (2x – 1) = 0 или log 4 x – 2 = 0.
1) log 4 ( 2x – 1) = 0, 2x – 1 = 1, x1 = 1.
2) log 4 x – 2 = 0, log4x = 2, x2 = 16.
Проверка показывает, что оба значения x являются корнями исходного уравнения.
Ответ. x1 = 1, x2 = 16.
Слайд 1412) Использование формулы перехода к новому основанию.
Пример.log3 x + log
x 3 = .
Уравнение имеет смысл при x >
0, x ≠1.(1)Воспользовавшись формулой log x 3 = ,
имеем: log3x + = .
Введем замену log3 x = t, t ≠ 0.
t + = , 2t2 – 5t + 2 = 0. t1 = 2, t2 = .
1) Если t1 = 2, то log 3 x = 2, x1 = 9.
2) Если t1 = , то log 3 x = , x2 = .
Найденные значения x удовлетворяют условиям (1) и являются корнями данного уравнения.
Ответ. x1 = 9, x2 = .
Слайд 15 13) Использование формулы log a b + log a с
= log a (bc).
Пример.log 2 (1 – x) = 3
– log 2 (3 – x)log 2 (1 – x) + log 2 (3 – x) = 3,
log 2((1 – x) (3 – x)) = 3,
(1 - x)(3 - x) = 8,
x2 - 4x - 5 = 0.
x1 = - 1, x2 = 5.
Проверка.
x1 = - 1.
Левая часть уравнения log 2 (1 – x) = log 2 (1 - (-1)) = log 2 2 = 1.
Правая часть уравнения 3 - log 2 (3 – x) = 3 - log 2 (3 - (-1)) =3 - log 2 4 = 3 - 2 = 1.
1 = 1 верно, x1 = - 1 корень исходного уравнения.
x2 = 5.
Число x2 = 5 не является корнем исходного уравнения, так как при x = 5 левая и правая части уравнения теряют смысл.
Ответ. x = - 1.
Слайд 1614) Использование формулы log a b - log a c
= log a (b/c)
Пример. lg (x - 1) –
lg (2x – 11) = lg 2.lg = lg 2,
= 2,
x – 1 = 2∙ (2x -11),
3x = 21, x = 7.
Проверка. x = 7.
lg (x - 1) – lg (2x – 11) = lg (7 - 1) – lg (2∙7 – 11) = lg 6 – lg 3 = lg 2.
lg 2 = lg 2 верно, x = 7 корень данного уравнения.
Ответ. x = 7.
Слайд 1715)Уравнения вида A∙( log a f (x))2 + B∙ log
a f (x) + C = 0 .
Уравнения вида A∙(
log a f (x))2 + B∙ log a f (x) + C = 0 .(f (x) > 0, а > 0,а ≠ 1) путем замены log a f (x) = t сводится к квадратному уравнению.
Пример. + = 5.
ОДЗ уравнения х > 0.
2 + = 5,
2 + = 5,
2∙ - 2 + - 4∙ + 4 - 5 = 0,
- 2∙ - 3 = 0.
Обозначив = t, получим квадратное уравнение: t2 - 2t - 3 = 0,
корни которого t1 = - 1, t2 = 3
Возвращаясь к переменной х, рассмотрим два случая:
1) = -1, х1 = 3.
2) = 3, х2 = . Оба значения входят в ОДЗ.
Ответ. х1 = 3 , х2 = .
Слайд 1816) Показательно - логарифмические уравнения.
Если в уравнении содержится выражение вида
, то для
нахождения корней
уравнения необходимо сначала прологарифмироватьобе его части по тому же основанию, что и основание логарифма,
стоящего в показателе степени, а затем решить получаемое
алгебраическое уравнение относительно log a x.
Пример. = 4.
ОДЗ уравнения: x > 0, x ≠ 1.
Прологарифмируем обе части уравнения по основанию 2:
= log 2 4, (log 2 x - 1)∙log 2 x = 2, ( log 2 x)2 - log 2 x - 2 = 0.
Пусть log 2 x = t , тогда t2 - t - 2 = 0, откуда t = 2, t = -1,
Возвращаясь к переменной х, рассмотрим два случая:
1) log 2 x = 2, x1 = 4.
2) log 2 x = - 1, x2 = . Оба значения удовлетворяют ОДЗ.
Ответ. x1 = 4, x2 = .
Слайд 1917)Использование однородности.
Уравнения вида a∙A2(х)+ b∙A(х)B(х) + c∙B2(х) = 0 называются
однородными
Способ решения однородных уравнений:
деление обеих частей уравнения на A2(х),
A(х)B(х) или B2(х) и введение замены.Пример. lg2(x + 1) = lg(x + 1) lg(x - 1) + 2 lg2(x - 1).
ОДЗ x > 1, lg2(x + 1) - lg(x + 1) lg(x - 1) - 2 lg2(x - 1) = 0,
Разделим на lg2(x - 1) ≠ 0.
- - 2 = 0. Пусть у = ,
тогда у2 – у – 2 = 0, откуда у1 = 2, у2 = -1.
Возвращаясь к переменной х, рассмотрим два случая:
1) = 2; lg(x + 1) = 2 lg(x - 1); lg(x + 1) = lg(x - 1)2; х + 1 = (х – 1)2;
х + 1 = x2 - 2х + 1 ; x2 - 3х = 0; (x – 3)х = 0. x1 = 3, x2 = 0.
x = 0 не удовлетворяет ОДЗ.
2) = -1;lg(x + 1) = - lg(x - 1); lg(x + 1) = lg ; x + 1 = ; x2 – 1= 1; x2= 2. x1,2 =
x = не удовлетворяет ОДЗ.
Ответ. x1 = 3, x2 = .
Слайд 2018) Уравнения вида a loga f(x) = g(x).
Уравнение вида
= g(x) равносильно
системе:Пример. = 4x.
Ответ. x = 1.
Слайд 2119) Уравнения вида a logс f(x) = b.
Уравнения вида
= b
равносильно уравнению = am , где b = am;откуда log c f(x) = m.
Пример. 23lg x∙5lg x = 1600.
8lg x∙5lg x = 1600, 40lg x = 1600, 40lg x = 402, lg x = 2,
x = 100.
Ответ. x = 100.
Слайд 2220) Уравнения вида a(x) loga(x) f(x) = g(x).
Уравнение вида
= g(x) равносильно системе:
Пример. = 2x.
Ответ. x = 3.
Слайд 2321) Использование формул loga(b/c) = log a |b| - log
a |c|, loga(b∙c) = log a |b| + log a
|c|.Пример. = + 1.
Ответ. x = -2.
Слайд 2422) Использование формулы log f(x) (g(x))n = n∙ log f(x)
|g(x)|
(При четном n).
Пример. lg4(x - 1)2 + lg2(1
- x)3 = 25.24∙ lg4|x - 1| + 32∙ lg2(1 - x) = 25.
Область определения функции lg2(1 - x) «диктует» выполнение неравенства 1 – x > 0. Поэтому |x - 1| = 1 – x.
В полученном уравнении 16∙ lg4(1 - x) + 9∙ lg2(1 - x) - 25 = 0 сделаем замену переменной: у = lg2(1 - x), у ≥ 0.
у = 1.
Следовательно, lg2(1 - x) = 1. Откуда:
1) lg(1 - x) = 1; lg(1 - x) = lg10; 1 – x = 10; x1 = - 9.
2) lg(1 - x) = - 1; lg(1 - x) = lg 0,1; 1 – x = 0,1; x2 = 0,9. Ответ. x1 = - 9, x2 = 0,9.
Слайд 2523) Рационально – логарифмические уравнения.
Пример.
+
= 1.Сделав замену lg x = у, получаем + = 1.
Умножим обе части уравнения на общий знаменатель
(4 + у)(2 – у) ≠ 0.
2 – у + 8 + 2у = 8 – 2у – у2, у2 + 3у + 2 = 0. у1 = -1, у2 = - 2.
Возвращаясь к переменной х, рассмотрим два случая:
1) lg x = -1, х = 0,1.
2) lg x = -2, х = 0,01. Оба значения удовлетворяют ОДЗ.
Ответ. х1 = 0,1, х2 = 0,01.
Слайд 2624) Иррационально – логарифмические уравнения.
1 случай
Пример.
= log 2 (2x).
ОДЗ x > 0.
= log 2 2 + log 2 x, = 1 + log 2 x.
Сделав замену переменной log 2 x = у, получаем = 1 + у. (*)
Возведя обе части уравнения в квадрат, имеем: 2у2 + 3у – 5 = 1 + 2у + у2,
у 2+ у – 6 = 0. у1 = - 3, у2 = 2.
Проверим иррациональное уравнение (*) .
1) При у1 = - 3 правая часть уравнения отрицательна, следовательно у1 = - 3 посторонний корень.
2) у2 = 2.
Левая часть = = = 3.
Правая часть 1 + у = 1 + 2 = 3.
3 = 3 верно, у = 2 корень уравнения (*).
Возвращаясь к переменной х, имеем: log 2 x = 2, х = 4.
Ответ . х = 4.
Слайд 2724) Иррационально – логарифмические уравнения.
2 случай
Пример .
+
= 4lg x – 5.Так как квадратный корень всегда неотрицателен, то левая часть уравнения неотрицательна при любых x, и, следовательно, правая часть 4lg x – 5 ≥ 0.
Тогда = | 5 - 4lg x | = 4lg x – 5,т.е. исходное уравнение равносильно системе:
Решением последней системы являются x, удовлетворяющие уравнению lg x = 4, т.е. x = 104, x = 10000.
Ответ. x = 10000.
Слайд 2825) Уравнения, содержащие модуль.
1случай
Пример.
= .
1) При 0 ≤ x < 1:| - 1| = 1- , поскольку < 1 при 0 ≤ x < 1.
Уравнение равносильно системе:
0 ≤ x < 1.
2) При x ≥ 1:| - 1| = - 1, поскольку ≥ 1 при x ≥1.
Уравнение равносильно системе:
x1= 4 , x2= 1.
Ответ. Корнями уравнения являются числа из промежутка 0 ≤ x ≤ 1 и x = 4.
Слайд 2925) Уравнения, содержащие модуль.
2 случай
Пример . 3+ |2 – log
5 x| = |1 + log 5 x |.
Сделаем замену
t = log5 x и решим уравнение: 3 + |2 - t| = |1 + t|.Критические точки t = 2, t = - 1.
При t < - 1: 3 + 2 - t = - (1 + t), откуда 5 - t = - t - 1,
0∙t = - 6 нет корней.
При - 1 ≤ t < 2: 3 + 2 - t = 1 + t , откуда 5 - t = t + 1, -2t = - 4,
t = 2- не удовлетворяет условию - 1 ≤ t < 2.
При t ≥ 2: 3 + t – 2 = 1 + t , откуда t +1 = t + 1, 0∙t = 0. Следовательно, t ≥ 2.
Итак, log 5 x ≥ 2, log 5 x ≥ log 5 25, так как 5 > 1, то x ≥ 25.
Ответ. x ≥ 25.
Слайд 3025) Уравнения, содержащие модуль.
3 случай
Пример.
= 2.
ОДЗ: x ≠3.
x2 – 6x + 14 = (x2 – 6x +9) + 5 = (x – 3)2 + 5 = | x – 3|2 + 5.
сделаем замену переменной t = | x – 3|.
= 2; = ; t2 + 5 = ( t + 1)2; t2 + 5 = t2 + 2t + 1; 2t = 4; t = 2.
Возвращаясь к переменной x, имеем: | x – 3| = 2, откуда
x – 3 = 2 или x – 3 = - 2,
т.е. x1= 5, x2 = 1.
Проверка показывает, что оба значения x являются корнями исходного уравнения.
Ответ. x1= 5, x2 =1.
Слайд 3126) Комбинированные уравнения.
Пример 1.
+ 3∙
= 10.Преобразуем выражение :
= = = .
Сделав теперь в исходном уравнении замену переменной
t = , придем к системе:
t = 2.
Итак, = 2.
Прологарифмируем это уравнение по основанию 2:
= log 2 2, ( log 2 4x)2 = 1.
log 2 4x = 1 или log 2 4x = - 1.
1) log 2 4x = 1, 4x = 2, x1 = .
2) log 2 4x = -1, 4x = , x2 = .
Ответ. x1= , x2 = .
Слайд 3226) Комбинированные уравнения.
Пример 2.
=
.ОДЗ: x < 0, x > 4.
В соответствии со свойствами логарифмов =
исходное уравнение преобразуется в показательное:
= ,
откуда = ,
log 3 5 = 4( log 3 15 - log 3 (x2 – 4x)),
log 3 5 = 2log 3 15 - log 3 (x2 – 4x),
log 3 (x2 – 4x) = log 3(225/5),
x2 – 4x = 45, x2 – 4x – 45 = 0.
x1 = 9 или x2 = - 5.
Ответ. x1= 9 , x2 = - 5.
Слайд 3326) Комбинированные уравнения.
Пример 3. log cos x sin
x + log sin x cos x = 2.
ОДЗ:
2 n < x < + 2 n, n Z.(*)
Пусть log cos x sin x = у, тогда log sin x cos x = .
у + = 2; = 0; у = 1.
log cos x sin x = 1; log cos x sin x = log cos x cos x;
sin x = cos x; tg x = 1; x = + n, n Z.
Учитывая ограничения (*), имеем: x = +2 n, n Z.
Ответ. x = +2 n, n Z.
Слайд 3427) Оценочная «граничная» задача.
Производится оценка множеств значений правой и левой
частей уравнения. Если правая часть ограничена снизу, а левая часть
ограничена сверху, то равенство возможно только в общей точке.Пример. = log2x + log x2.
Так как log2x + log x2 = log2x + , то при всех x > 0, x ≠ 1 выполняется неравенство |log2x + log x2| ≥ 2.
С другой стороны, - x2 + 4x – 3 = - x2 + 4x – 4 +1= - (x – 2)2 + 1 ≤ 1 при любом x, откуда следует, что ≤ 21 = 2.
Поэтому равенство левой и правой частей исходного уравнения возможно лишь в случае
Решим второе уравнение:
= 2, - x2 + 4x – 3 = 1, - (x – 2)2 + 1 = 1, - (x – 2)2 = 0, x = 2.
Подставим найденное значение x = 2 в первое уравнение системы:
log22 + log 22 = 1 + 1 = 2. 2 = 2 – верно.
x = 2 – корень исходного уравнения.
Ответ. x = 2.
Слайд 3528) Использование монотонности функций.
Пример. log7(x + 8) = - x.
По
определению логарифма имеем: x + 8 = 7-x;
x + 8 = .(*)Функция у = x + 8 – возрастающая, функция у = - убывающая, следовательно, по теореме о встречной монотонности уравнение (*) имеет не более одного корня.
Подбором находим, что это x = - 1.
Ответ. x = -1.
Слайд 36
Литература:
1) Алгебра. ЕГЭ: шаг за шагом / А.А.Черняк, Ж.А.Черняк.- Волгоград:
Учитель,2012.
2) Методы решения задач по математике: Пособие для поступающих в
НПИ. Ч1 / Ред. журн. «Изв. вузов. Электромеханика». Новочеркасск,19933) Алгебра и начала математического анализа, 10-11 класс, В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений (базовый уровень) / А.Г. Мордкович, – 12-е изд., доп.-– М. : Мнемозина, 2011.
4) Алгебра и начала математического анализа, 10-11 класс, Учебник для учащихся общеобразовательных учреждений (базовый уровень) /Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачёва и др.- 16-е изд.,перераб. - М.:Просвещение,2010
5)Математика. Учебное пособие для слушателей подготовительных курсов /Ю.С.Рогозина, И.М.Башняк, О.Л.Логвиненко, Новочеркасск: НГМА ,2003