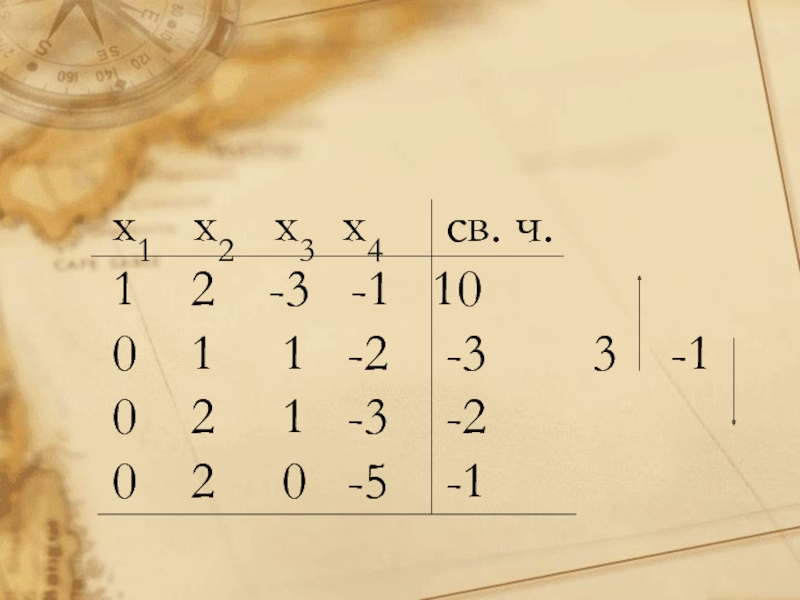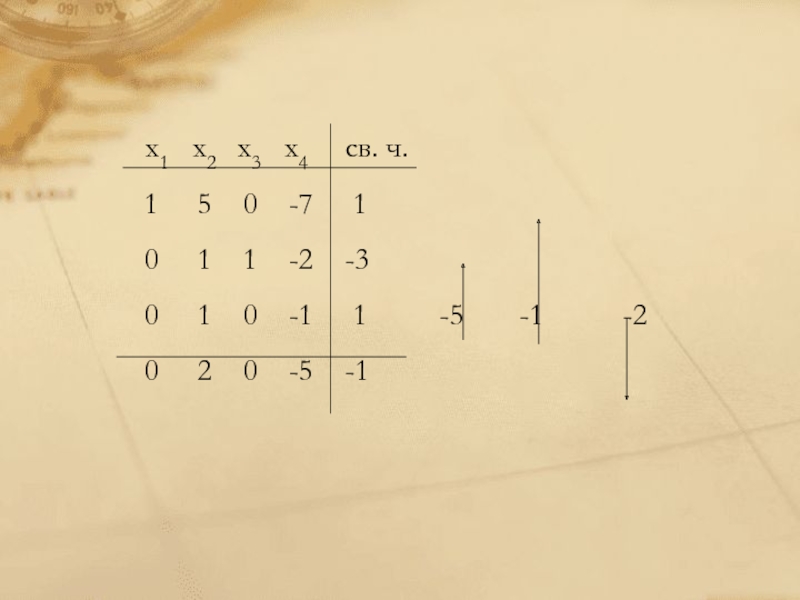Решение систем уравнений методом Жордана-Гаусса и Крамера

с n неизвестными в общем случае записывается так:

a11x1+a11x2+…+a1nxn

=b1
a21x2+a22x2+…+a2nxn =b2 (1)
……………………………
am1x1+am2x2+…+amnxn =bm
Коэффициенты {aij} i=1,2,…m, j=1,2,…n, и свободные члены {bi} i=1,2..m, - заданные действительные числа. Первый индекс i в записи aij указывает на номер уравнения, второй – j – номер неизвестной.
Решить систему (1) означает найти все её решения, т.е. все такие наборы чисел (x1, x2, …xn), которые при подстановке во все уравнения системы превращают каждое из них в верное равенство, или доказать, что решений нет.
Система (1) называется:
-совместной, если имеет хотя бы одно решение;
-определенно совместной, если имеет только одно решение;
-неопределенно совместной, если имеет более одного решения;
-несовместной, если не имеет ни одного решения.

= -23
2x1+6x2-5x3-5x4 = 18
x1+3x3+4x4 = -11

таблицы Гаусса данной системы имеет вид (св.ч. означает «свободные члены»

уравнений системы, вертикальная черта заменяет знаки равенства):
x1 x2 x3 x4 св.ч.
1 2 -3 -1 10 2 -2 1
-2 -3 7 0 -23
2 6 -5 -5 18
-1 0 3 -4 -11

столбец, выбирая в качестве ведущего коэффициента a11 = 1 (в

таблице он обведен кружком). Для этого над строками таблицы (над уравнениями системы) выполним следующие действия (они обозначены справа от таблицы): 1) первую строку сохраняем (переписываем); 2)первую строку, умноженную на 2, прибавим ко второй; 3)первую строку, умноженную на -2, прибавим к третьей; 4)первую строку прибавим к четвертой. Получим второй блок таблицы.

1 2 -3 -1 10 0

1 1 -2 -3 3 -1 0 2 1 -3 -2 0 2 0 -5 -1

один «0». Ведущий коэффициент a23 = 1 обведен кружком. Далее:
1)

вторую строку, умноженную на 3, прибавим к первой и запишем вместо первой строки;
2) перепишем вторую строку без изменения;
3) вторую строку, умноженную на -1, прибавим к третьей;
4) четвертую строку перепишем без изменения.
Именно эти действия выражаются числами и стрелками, показанными справа от второго блока таблицы. Третий блок таблицы имеет вид:

1 5 0 -7 1

0 1 1 -2 -3
0 1 0 -1 1 -5 -1 -2
0 2 0 -5 -1

этого принимаем в качестве ведущего коэффициента a23 = 1, и

выполним следующие действия: третью строку, умноженную на -5, -1, -2, прибавим к первой, второй и четвертой строкам соответственно. Третью строку переписываем без изменений. Получаем четвертый блок:

x1 x2 x3 x4 св. ч.
1 0 0 -2 -4
0 0 1 -1 -4
0 1 0 -1 1
0 0 0 -3 -3

a44 =-3. Четвертую строку разделим на -3. Остальные действия

считаем очевидными. Получаем:

x1 x2 x3 x4 св. ч.
1 0 0 0 -2
0 1 0 0 2
0 0 1 0 -3
0 0 0 1 1

всех неизвестных (r = m = n = 4): x1 =

-2, x2 = 2, x3 = -3, x4 = 1 Запишем это также в виде: x = (-2,2,-3,1). Система однозначно совместна. Примечание. Подставьте эти значения неизвестных в данную систему и убедитесь, что получаются верные числовые равенства.

Упражнения.
1. x1+3x2-5x3=-1
2x1-x2+3x3=4
3x1+2x2-5x3=0
Ответ: x =(1, 1, 1)
2. x1-3x2+2x3-3x4-2x5=4
x1-x2-x3-x4+x5=1
x1+2x2+x4+3x5=-6
3x1-2x2+x3-3x4+2x5=0
Ответ: система несовместна.

x1-2x2-x3+2x4=7
2x1-x2+3x3-x4 =

5
3x1-3x2+2x3+x4=10
Ответ: несовместна.