Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема: Задачи на совместную работу
Содержание
- 1. Тема: Задачи на совместную работу
- 2. Саша убирает кабинет математики за 20 минут. Какую часть работы он выполняет за 1 минуту?1/20
- 3. Мастер может выполнить весь заказ за 4
- 4. Во дворе заливают каток. За 1 час
- 5. Бассейн наполняется водой за 10ч. Какая часть
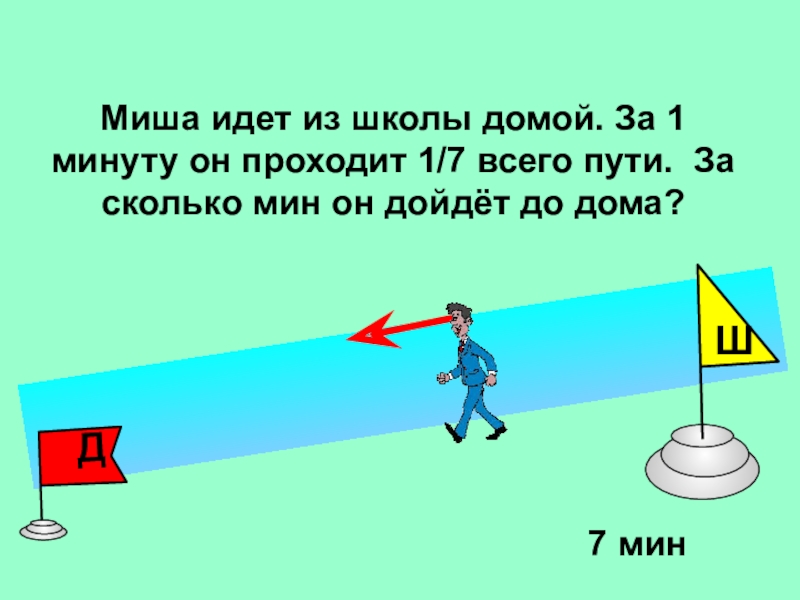
- 6. Миша идет из школы домой. За 1
- 7. Задача про ёлочные игрушки
- 8. Задача про ёлочные игрушки
- 9. Алгоритм решения задач на совместную работу 1.
- 10. Задача про КарлсонаКарлсон съедает банку варенья за
- 11. Примем всё варенье за 1.
- 12. Задача про Тома Сойера.
- 13. Примем всю работу за 1.
- 14. Решение.Примем всю работу за 1.1) 1 :
- 15. Задача на одновременное движение?Из двух посёлков одновременно
- 16. Алгоритм решения задач на совместную работу 1.
- 17. Скачать презентанцию
Саша убирает кабинет математики за 20 минут. Какую часть работы он выполняет за 1 минуту?1/20
Слайды и текст этой презентации
Слайд 3Мастер может выполнить весь заказ за 4 дня, а ученик
– за 7 дней. Какую часть работы они выполнят вместе
за 1 день?Слайд 4Во дворе заливают каток. За 1 час залили 1/5 катка.
За сколько часов зальют весь каток?
За 5 часов
Слайд 6Миша идет из школы домой. За 1 минуту он проходит
1/7 всего пути. За сколько мин он дойдёт до дома?
Ш
7
минСлайд 7Задача про ёлочные игрушки
На фабрике
ёлочных игрушек мастер за 1 час расписывает 15игрушек, а его
ученик 10 игрушек. Сколько игрушек за 1 час они расписывают вместе? За сколько часов они распишут 150 игрушек?Решение.
1)15+10=25(игр.за 1 час) распишут
мастер и ученик вместе;
2) 150:25=6(часов)- за столько
часов мастер и ученик распишут
150 игрушек.
Ответ: 1)25 игрушек в час;
2)за 6 часов.
Слайд 8Задача про ёлочные игрушки
1) На фабрике
ёлочных игрушек мастер расписывает 150 игрушек за 10 часов, а
его ученик 150 игрушек за 15 часов. За сколько часов они распишут 150 игрушек, работая вместе?2) На фабрике ёлочных игрушек
мастер расписывает игрушки
за 10 часов, а его ученик
выполняет эту же работу
за 15 часов.
За сколько часов они
распишут игрушки,
работая вместе?
Слайд 9Алгоритм
решения задач на совместную работу
1. Всю работу (
Всё, что надо сделать; говорят, весь объём работы) принимаем за
1,2. Находим скорость работы - часть работы, выполненную за единицу времени
3. Находим время работы
Слайд 10Задача про Карлсона
Карлсон съедает банку варенья за 3 мин, фрекен
Бок – за 10 мин, а Малыш – за 15
мин. За сколько минут они съедят банку варенья втроём?Слайд 11 Примем всё варенье за 1.
1. Какую часть банки съедает Карлсон за1 минуту?
2. Какую часть банки съедает фрекен Бок за 1 минуту?
3. Какую часть банки съедает Малыш за 1 минуту?
4. Какую часть банки съедают Карлсон,
фрекен Бок и Малыш втроём за 1 минуту?
5. За сколько минут они съедят банку варенья
втроём?
Слайд 12 Задача про Тома Сойера.
Том Сойер
и Гек Финн вместе красят забор за 9 часов.Том и
Бекки Тэтчер вместе красят забор за 18 часов. Гек и Бекки вместе - за 12 часов. За сколько часов Том, Гек и Бекки покрасят забор, если будут работать втроём?Слайд 13Примем всю работу за 1.
1. Какую часть работы выполнят Том и Гек, работая вместе, за 1 час?
2. Какую часть работы выполнят Том и Бетти, работая вместе, за 1 час?
3. Какую часть работы выполнят Гек и Бетти, работая вместе, за 1 час?
4. Чему равна удвоенная часть работы , которую выполнят Том, Гек и Бетти втроём за 1 час?
5. Чему равна часть работы , которую выполнят Том, Геки Бетти втроём за 1 час?
6. За сколько часов Том, Гек и Бетти покрасят забор втроём?
Слайд 14Решение.
Примем всю работу за 1.
1) 1 : 9 =
(работы) выполнят Том и Гек вместе за 1 ч
;2) 1 :18 = (работы) выполнят Том и Бекки вместе за 1 ч;
3) 1 : 12 = (работы) выполнят Гек и Бекки вместе за 1 ч ;
+ + = + + = = (работы)-
удвоенная часть совместной работы Тома, Гека и Бекки за 1 ч;
: 2 = ( работы) выполнят Том, Гек и Бекки за 1 ч ;
6) 1 : = 8 (ч) – время работы Тома, Гека и Бекки .
Ответ : за 8 часов Том , Гек и Бекки покрасят забор, работая втроём.
Слайд 15Задача на одновременное движение?
Из двух посёлков одновременно навстречу друг другу
выехали два лыжника. Один проходит за час 1/10 всего пути,
а другой 1/15 всего пути.Через сколько часов они встретятся?
Решение.
Примем весь путь за 1.
1) 1/10+1/15=1/6(всего пути)- скорость сближения лыжников;
2)1:1/6= 6(часов)- время, через которое лыжники встретятся.
Ответ: через 6 часов
Слайд 16Алгоритм
решения задач на совместную работу
1. Всю работу (
Всё, что надо сделать; говорят, весь объём работы) принимаем за
1,2. Находим скорость работы - часть работы, выполненную за единицу времени
3. Находим время работы