Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение в гравитационном поле. Искусственные спутники Земли
Содержание
- 1. Движение в гравитационном поле. Искусственные спутники Земли
- 2. На этом уроке вы познакомитесь с …
- 3. Солнечная система – это комплекс небесных тел,
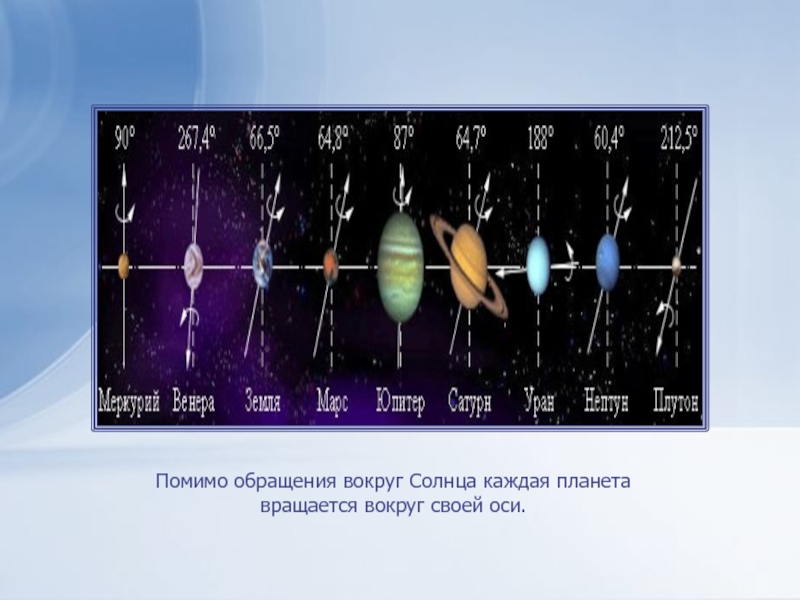
- 4. Помимо обращения вокруг Солнца каждая планета вращается вокруг своей оси.
- 5. По характеристикам планеты делятся на две группы.
- 6. Планеты-гиганты – Юпитер, Сатурн, Уран и Нептун
- 7. Малые планетыПомимо больших планет в Солнечную систему
- 8. Размеры Солнца во много раз превышают не
- 9. Иисак Ньютон смог объяснить движение тел в
- 10. Внутри Земли, если принять ее за однородный
- 11. Притяжение Луны и СолнцаКаждый день уровень океанских
- 12. Невозмущенное движение в гравитационном полеВ общем случае
- 13. Орбиты в поле тяготения
- 14. Любое тело в поле тяготения будет двигаться
- 15. ЭллипсЭллипс определяется как геометрическое место точек, для
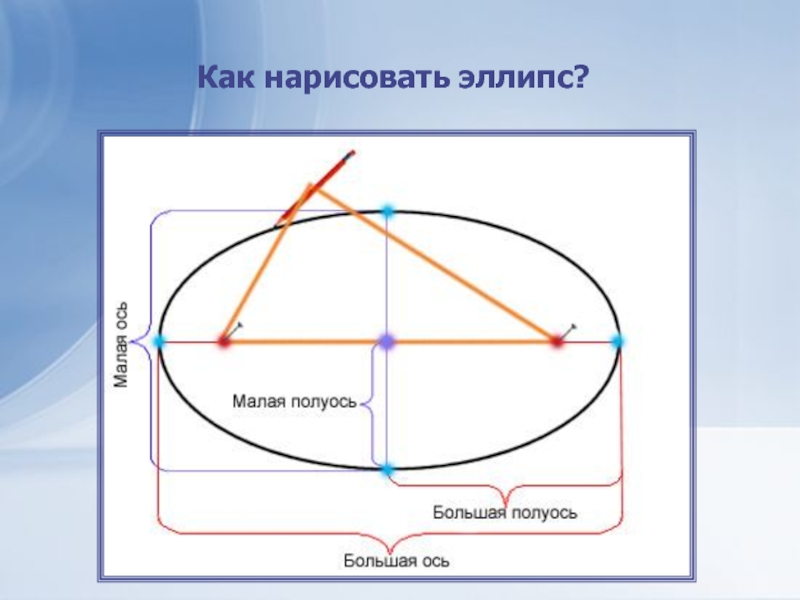
- 16. Как нарисовать эллипс?
- 17. Законы КеплераДинамическая модель иллюстрирует законы Кеплера на
- 18. Скорости близких к Солнцу планет значительно больше, чем скорости далеких
- 19. Движение спутника в гравитационном поле ЗемлиМодель иллюстрирует
- 20. Величина третьей космической скоростиВеличина третьей космической
- 21. Силы, действующие на космонавтов внутри космического корабля, вращающегося вокруг Земли
- 22. Система орбитальных элементовМодель демонстрируют основную систему координат,
- 23. Карта Центра управления полетом (ЦУП) Благодаря
- 24. Качественная интерпретация прецессии орбиты спутника в поле несферичной Земли
- 25. Изменение первоначально круговых орбитНа схемах приведено изменение
- 26. Торможение КА в атмосфере
- 27. Межпланетные перелетыМодель демонстрирует наиболее выгодную орбиту для
- 28. Маневр изменения плоскости орбитыЭффективность маневра изменения плоскости
- 29. Межпланетный перелет
- 30. Гравитационный (или пертурбационным) маневрГравитационным (или пертурбационным)
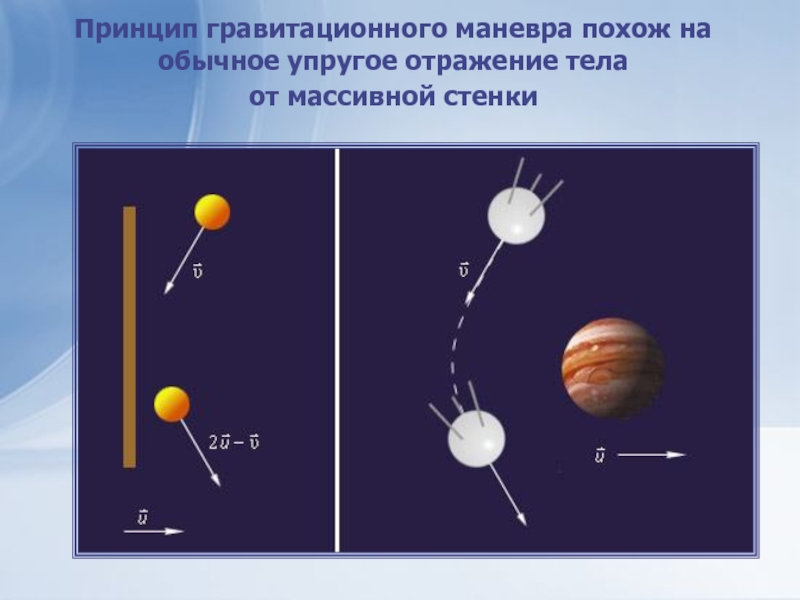
- 31. Принцип гравитационного маневра похож на обычное упругое отражение тела от массивной стенки
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Составлена учителями: Онучиной В.И.
Дмитриевой С.А.
Движение в гравитационном поле.
Исскуственные
спутники Земли
Н.А. Заболоцкого»Слайд 2На этом уроке вы познакомитесь с …
Солнечная система
Гравитация внутри Земли
Законы Кеплера
Движение спутников
Элементы орбиты спутникаМежпланетный перелет
Гравитационный маневр
Слайд 3Солнечная система – это комплекс небесных тел, объединенных происхождением, упорядоченностью
движения и общностью физических свойств. Центральным телом Солнечной системы является
Солнце. Вокруг него по эллиптическим орбитам вращаются девять больших планет.Солнечная система
Слайд 5По характеристикам планеты делятся на две группы. К планетам земной
группы, состоящим, в основном, из скалистых и металлических пород и
имеющим небольшие размеры, относятся Меркурий, Венера, Земля и Марс.Характеристики планет
Слайд 6Планеты-гиганты – Юпитер, Сатурн, Уран и Нептун – расположены дальше
от Солнца; их металлические ядра окутывает плотная атмосфера из водорода,
гелия и других газов.Характеристики планет
Характеристики планет
Слайд 7Малые планеты
Помимо больших планет в Солнечную систему входят малые планеты
(астероиды), составляющие два пояса; один из них находится между орбитами
Марса и Юпитера, а второй – пояс Койпера, – за орбитой Нептуна. В настоящее время полагают, что Плутон является одним из объектов пояса Койпера. Далеко за поясом Койпера находится еще одно пылевое облако – облако Оорта. Кроме того, в Солнечную систему входят многочисленные кометы, облетающие Солнце по сильно вытянутым орбитам, межпланетная пыль и газ.Слайд 8Размеры Солнца во много раз превышают не только размеры больших
планет, но и расстояния от большинства спутников до планет. Радиус
Солнца в 109 раз, а масса – в 330 000 раз больше радиуса и массы Земли.Слайд 9Иисак Ньютон смог объяснить движение тел в космическом пространстве с
помощью закона всемирного тяготения. Ньютон пришел к своей теории в
результате многолетних исследований движения Луны и планетУскорение, которое испытывает тело m, находящееся на расстоянии r от тела M, равно
Вблизи поверхности Земли ускорение свободного падения равно g = 9,8 м/с2. Сплюснутость Земли и ее вращение приводят к отличию силы тяжести на экваторе и возле полюсов: ускорение свободного падения в точке наблюдения может приближенно высчитываться по формуле g = 9,78 ∙ (1 + 0,0053 sin φ), где φ – широта этой точки.
Слайд 10Внутри Земли, если принять ее за однородный шар, сила тяжести
убывает пропорционально расстоянию до центра:
Модель показывает, как изменяется сила
тяжести внутри Земли. Из теоремы Гаусса следует, что если считать Землю однородным шаром, сила тяжести внутри ее уменьшается пропорционально расстоянию до центра.
Слева изображена Земля (ее правая половина показана в разрезе так, что виден туннель, проходящий на расстоянии L от центра; это расстояние можно менять). В правом нижнем углу изображен график зависимости ускорения свободного падения от расстояния до центра Земли. Серая линия отмечает радиус Земли, равный 6371 км.
При нажатии кнопки Старт в туннель начинает падать тело. Силы трения, а также вращение Земли в модели не учитываются. Тело летит к центру туннеля под действием силы тяжести.
Пройдя середину тоннеля на максимальной скорости, оно начинает замедляться. Достигнув противоположной точки туннеля, тело останавливается и начинает падать обратно, совершая таким образом колебательные движения. График зависимости ускорения тела от времени приведен справа вверху.
Движение тела можно приостановить или прекратить при помощи кнопок Стоп и Сброс.
Слайд 11Притяжение Луны и Солнца
Каждый день уровень океанских вод поднимается и
снижается, причем в устьях некоторых рек и отдельных заливах на
несколько метров. Эти явления носят название приливов и отливов. Гидросфера, как и всякое жидкое тело, способна деформироваться, что и происходит каждый день в результате притяжения Луны и Солнца. Луна каждые 24 часа 50 минут вызывает приливы не только в океанах, но и в коре Земли, и в атмосфере. Под воздействием приливных сил литосфера вытягивается примерно на полметра.Слайд 12Невозмущенное движение в гравитационном поле
В общем случае невозмущенное движение в
гравитационном поле определяется законом сохранения энергии, то есть K + U = сonst, где
– кинетическая энергия тела массой m, движущегося со скоростью υ, – потенциальная энергия этого тела, находящегося на расстоянии r от тела массой M. Константа h называется постоянной энергии.Слайд 14Любое тело в поле тяготения будет двигаться по коническому сечению
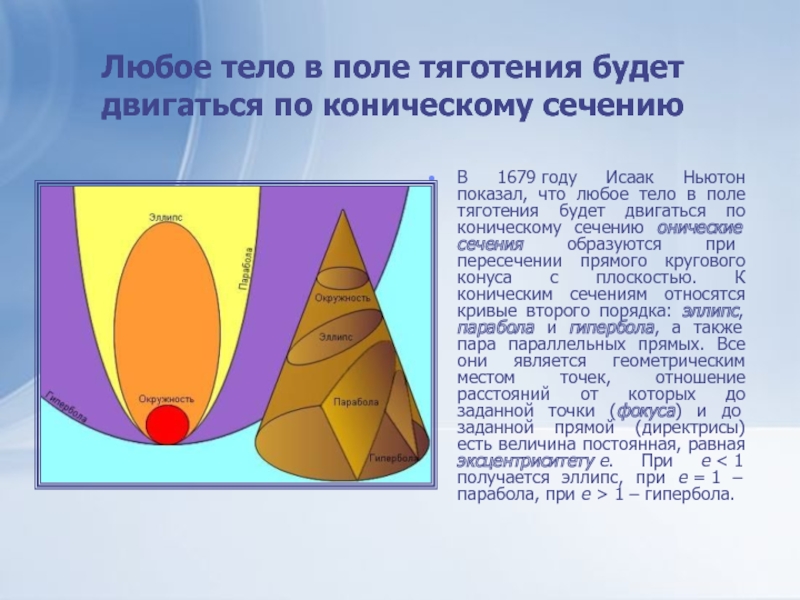
В
1679 году Исаак Ньютон показал, что любое тело в поле тяготения
будет двигаться по коническому сечению онические сечения образуются при пересечении прямого кругового конуса с плоскостью. К коническим сечениям относятся кривые второго порядка: эллипс, парабола и гипербола, а также пара параллельных прямых. Все они является геометрическим местом точек, отношение расстояний от которых до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная, равная эксцентриситету e. При e < 1 получается эллипс, при e = 1 – парабола, при e > 1 – гипербола.Слайд 15Эллипс
Эллипс определяется как геометрическое место точек, для которых сумма расстояний
от двух заданных точек (фокусов F1 и F2) есть величина
постоянная и равная длине большой оси: r1 + r2 = |AA´| = 2a. Степень вытянутости эллипса характеризуется его эксцентриситетом e. Эксцентриситет e = OF/OA. При совпадении фокусов с центром e = 0, и эллипс превращается в окружность.Большая полуось a является средним расстоянием от фокуса (планеты от Солнца): a = (AF1 + F1A')/2.
Слайд 17Законы Кеплера
Динамическая модель иллюстрирует законы Кеплера на примере движения спутника
Земли. Запуск модели производится кнопкой Старт, приостановка и возвращение в
исходное состояние – кнопками Стоп и Сброс соответственно. Группа переключателей Закон позволяет выбрать, какой закон Кеплера будет в настоящий момент иллюстрироваться.В центре окна вращается Земля. Вокруг нее по орбите движется спутник. Параметры орбиты (расстояние до Земли в перигее и начальную скорость) можно задать при помощи окон ввода в нижней части модели. В информационном окне приводятся прочие параметры орбиты: длина большой и малой полуосей, эксцентриситет и период обращения, а также виртуальное текущее время.
Первый закон Кеплера показывает, что все планеты движутся по эллипсу. Изменением начальной скорости небесного тела вы можете превратить эллиптическую орбиту в гиперболическую: по гиперболическим орбитам мимо Солнца движутся некоторые кометы и ряд спутников, покидающих пределы Солнечной системы.
Второй закон Кеплера показывает равенство площадей, заметаемых радиус–вектором небесного тела за равные промежутки времени. При этом скорость тела меняется в зависимости от расстояния до Земли (особенно хорошо это заметно, если тело движется по сильно вытянутой эллиптической орбите).
Демонстрация третьего закона Кеплера осуществляется при помощи двух спутников. В этом режиме можно задать параметры орбиты каждого спутника. Сравнив периоды обращения и радиусы орбит спутников, можно убедиться в справедливости закона.
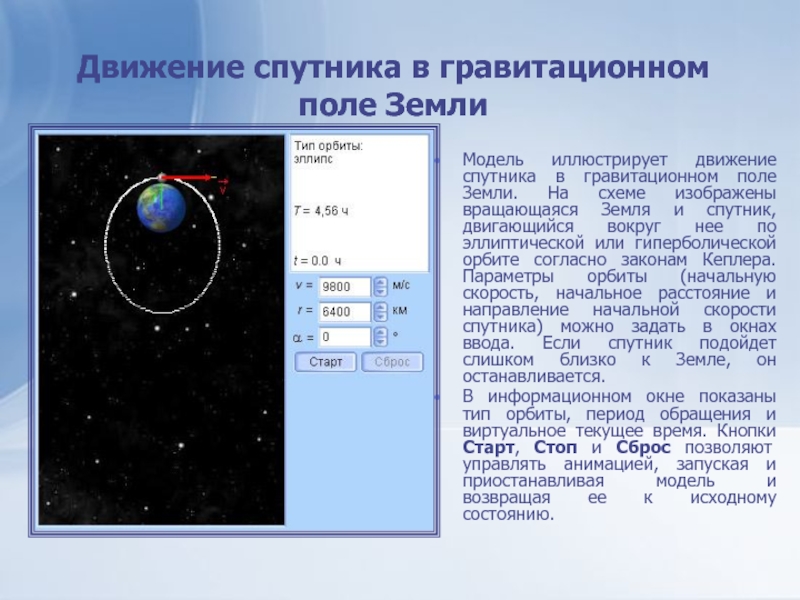
Слайд 19Движение спутника в гравитационном поле Земли
Модель иллюстрирует движение спутника в
гравитационном поле Земли. На схеме изображены вращающаяся Земля и спутник,
двигающийся вокруг нее по эллиптической или гиперболической орбите согласно законам Кеплера. Параметры орбиты (начальную скорость, начальное расстояние и направление начальной скорости спутника) можно задать в окнах ввода. Если спутник подойдет слишком близко к Земле, он останавливается.В информационном окне показаны тип орбиты, период обращения и виртуальное текущее время. Кнопки Старт, Стоп и Сброс позволяют управлять анимацией, запуская и приостанавливая модель и возвращая ее к исходному состоянию.
Слайд 20Величина третьей
космической скорости
Величина третьей космической скорости зависит от того,
в каком направлении корабль выходит из зоны действия земного тяготения
Слайд 22Система орбитальных элементов
Модель демонстрируют основную систему координат, применяемую для описания
положения искусственных спутников Земли, – систему орбитальных элементов. Шесть элементов
определяют положение и наклон орбиты относительно земного экватора, размеры орбиты и положение спутника на ней. Ось OX направлена на точку весеннего равноденствия.Если выключатель, соответствующий объекту системы, не выбран, этот объект отображается серым цветом. Если же его выбрать, то объект окрасится ярким цветом, а на схеме появится его название.
Слайд 23Карта Центра управления полетом (ЦУП)
Благодаря вращению Земли с космического
аппарата за короткое время можно увидеть большую часть поверхности земного
шара.Слайд 25Изменение первоначально круговых орбит
На схемах приведено изменение первоначально круговых орбит
импульсами, направленными «по скорости» и «против скорости». Как видно из
схем, орбита испытывает наибольшее геометрическое смещение в области, противолежащей точке, в которой телу был сообщен импульсСлайд 27Межпланетные перелеты
Модель демонстрирует наиболее выгодную орбиту для межпланетных перелетов.
Нажмите на
кнопку Старт. Ракета, обращающаяся вместе с Землей, включит двигатели и
выйдет на промежуточную эллиптическую орбиту (эллипс Гомана). При достижении афелия двигатели включаются еще раз, и космический аппарат перейдет на орбиту Марса. Время старта должно быть точно рассчитано, чтобы в тот момент, когда межпланетная станция перейдет на марсианскую орбиту, планета оказалась в том же месте.Кнопки Стоп и Сброс приостанавливают модель и возвращают ее в исходное состояние. Если выбрать теперь при помощи соответствующего переключателя перелет с Марса на Землю, все произойдет в обратном порядке: находясь на орбите Марса, аппарат получит импульс торможения и перейдет на промежуточную эллиптическую орбиту; второй импульс торможения в перигелии промежуточной орбиты переведет его на орбиту Земли.
Слайд 28Маневр изменения плоскости орбиты
Эффективность маневра изменения плоскости орбиты зависит от
того, в какой точке орбиты он выполняется
Слайд 30Гравитационный
(или пертурбационным) маневр
Гравитационным (или пертурбационным) маневром называется маневр космического
аппарата в поле тяжести планеты с целью увеличения собственной скорости
аппарата.В центре модели на фоне звездного неба показано небесное тело, в гравитационном поле которого производится маневр. Его можно выбрать из списка Планеты (можно выбрать Солнце, Луну и 9 больших планет Солнечной системы).
Модель запускается кнопкой Старт. При этом справа на прицельном расстоянии с начальной скоростью v0 начинает двигаться космический аппарат. Пролетая мимо планеты, он разворачивается на угол φ (его значение можно посмотреть в информационном окне) или сталкивается с поверхностью планеты (если прицельное расстояние или начальная скорость слишком малы). При помощи окон ввода Начальная скорость и Прицельное расстояние можно менять параметры движения космического аппарата, а кнопки Стоп и Сброс приостанавливают анимацию и возвращают модель к исходному состоянию.
Помимо разворота космического корабля, маневр может использоваться для увеличения его собственной скорости. Этот эффект сходен с эффектом увеличения скорости шарика после удара с массивной упругой стенкой, движущейся ему навстречу. Если скорость шарика до удара была v, а стенки –u, то после удара шарик приобретает скорость 2u + v (это становится ясным, если перейти в систему отсчета, связанную со стенкой). Спутник же увеличивает свою скорость, когда разворачивается вокруг планеты, двигающейся ему навстречу.