Законы движения планет

Содержание

1. Законы движения планет
2. Конфігурації планет
3. Конфігурації планет визначають розташування планет відносно Землі
4. Конфігураціями планет називають характерні взаємні положення планет відносно Землі й Сонця.
5. На рис. зображено протистояння (ПС) Марса (М1)
6. Протистояння — планету видно з Землі цілу ніч у протилежному від Сонця напрямку
7. Орбіти двох планет, Меркурія та Венери, розташовані
8. У положенні, коли Венера чи Меркурій знаходяться
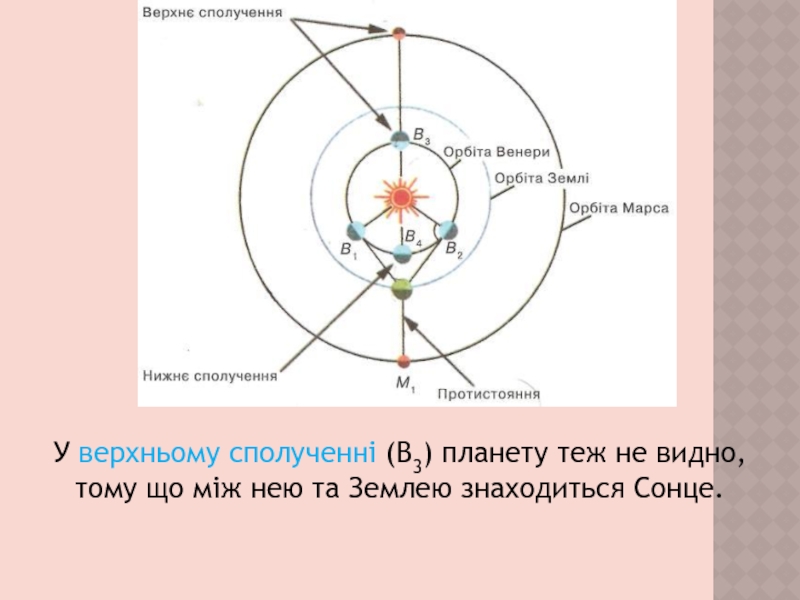
9. У верхньому сполученні (В3) планету теж не видно, тому що між нею та Землею знаходиться Сонце.
10. Найкращі умови для спостереження Венери та Меркурія бувають у конфігураціях, які називаються елонгаціями.
11. Елонгація — кутова відстань між планетою і Сонцем
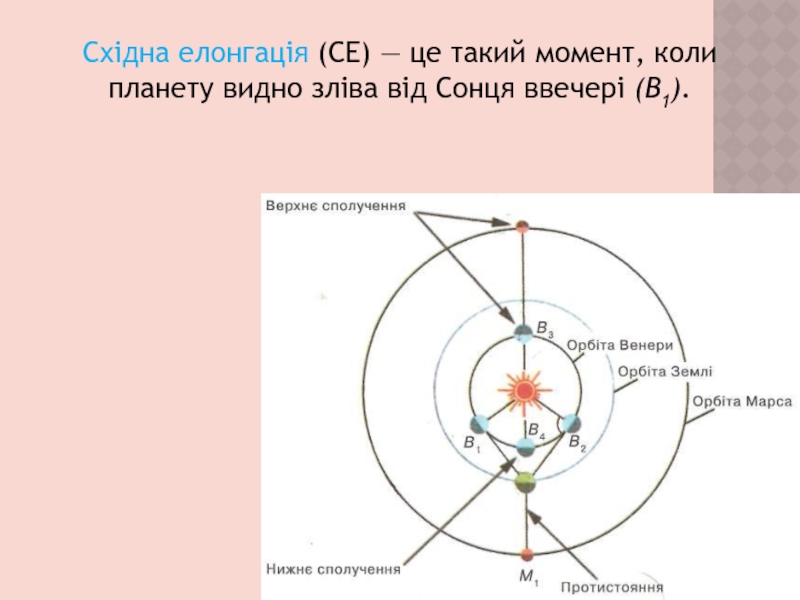
12. Східна елонгація (СЕ) — це такий момент, коли планету видно зліва від Сонця ввечері (B1).
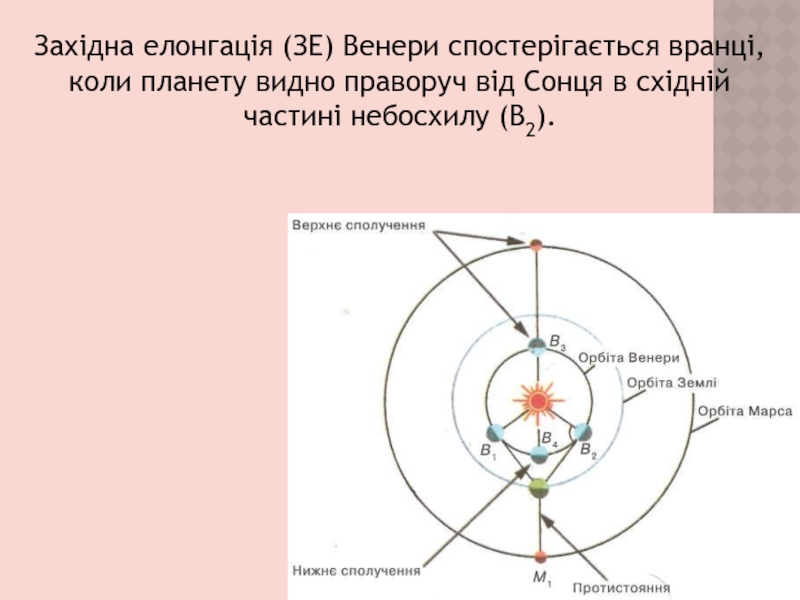
13. Західна елонгація (ЗЕ) Венери спостерігається вранці, коли
14. Закони Кеплера
15. Йоган Кеплер визначив, що Марс рухається навколо
16. Перший закон Кеплера:Всі планети обертаються навколо Сонця
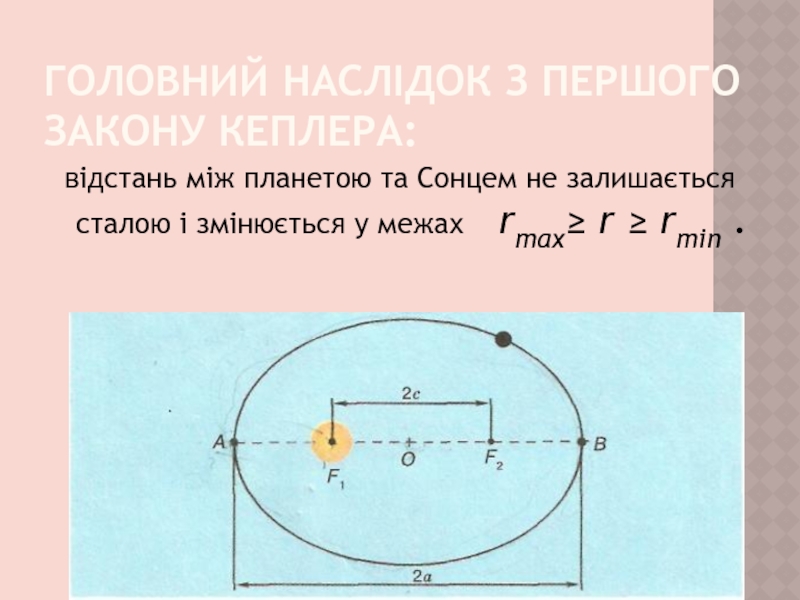
17. Головний наслідок з першого закону Кеплера:відстань між
18. Точка А орбіти, де планета підлітає найближче
19. Сума відстаней від планети до Сонця в
20. Земля в перигелії З—4 січня на найменшій
21. Супутники планет теж рухаються по еліптичних орбітах, причому у фокусі кожної орбіти знаходиться центр відповідної планети.
22. Другий закон Кеплера:Радіус-вектор планети за рівні проміжки часу описує рівні площі.
23. Головний наслідок другого закону Кеплера: при рухові
24. Найбільшу швидкість планета має в перигелії, коли
25. Третій закон Keплера:Квадрати сидеричних періодів обертання планет навколо Сонця співвідносяться як куби великих півосей їх орбіт:
26. Великий англійський фізик та математик Ісаак Ньютон
27. Закон всесвітнього тяжіння У 1687 р. І.
28. У реальних умовах жодна планета не рухається
29. Завдяки дослідженням збурення орбіти планети Уран астрономи
30. Скачать презентанцию

Конфігурації планет

Слайды и текст этой презентации

Слайд 1Закони руху планет

Слайд 2Конфігурації планет

Слайд 3Конфігурації планет визначають розташування планет відносно Землі й Сонця та

обумовлюють їх видимість на небосхилі. Усі планети світяться відбитим сонячним

промінням, тому краще видно ту планету, яка знаходиться ближче до Землі, за умови, якщо до нас повернена її денна, освітлена Сонцем півкуля.

Слайд 4Конфігураціями планет називають характерні взаємні положення планет відносно Землі й

Сонця.

Слайд 5На рис. зображено протистояння (ПС) Марса (М1) тобто таку конфігурацію,

коли Земля буде знаходитися на одній прямій між Марсом та

Сонцем. У протистоянні яскравість планети найбільша, тому що до Землі повернена вся її денна півкуля

На рис. зображено протистояння (ПС) Марса (М1) тобто таку конфігурацію, коли Земля буде знаходитися на одній прямій

Слайд 6Протистояння — планету видно з Землі цілу ніч у протилежному

від Сонця напрямку

Слайд 7Орбіти двох планет, Меркурія та Венери, розташовані ближче до Сонця,

ніж Земля, тому в протистоянні вони не бувають.

Орбіти двох планет, Меркурія та Венери, розташовані ближче до Сонця, ніж Земля, тому в протистоянні вони не

Слайд 8У положенні, коли Венера чи Меркурій знаходяться найближче до Землі,

їх не видно, бо до нас повернена нічна півкуля планети

(рис., положення В4). Така конфігурація називається нижнім сполученням з Сонцем.

У положенні, коли Венера чи Меркурій знаходяться найближче до Землі, їх не видно, бо до нас повернена

Слайд 9У верхньому сполученні (В3) планету теж не видно, тому що

між нею та Землею знаходиться Сонце.

Слайд 10Найкращі умови для спостереження Венери та Меркурія бувають у конфігураціях,

які називаються елонгаціями.

Слайд 11Елонгація — кутова відстань між планетою і Сонцем

Слайд 12Східна елонгація (СЕ) — це такий момент, коли планету видно

зліва від Сонця ввечері (B1).

Слайд 13Західна елонгація (ЗЕ) Венери спостерігається вранці, коли планету видно праворуч

від Сонця в східній частині небосхилу (В2).

Слайд 14Закони Кеплера

Слайд 15Йоган Кеплер визначив, що Марс рухається навколо Сонця по еліпсу,

а потім було доведено, що й інші планети теж мають

витягнуті орбіти.

Йоган Кеплер визначив, що Марс рухається навколо Сонця по еліпсу, а потім було доведено, що й інші

Слайд 16Перший закон Кеплера:
Всі планети обертаються навколо Сонця по еліпсах, а

Сонце знаходиться в одному з фокусів цих еліпсів

Перший закон Кеплера:Всі планети обертаються навколо Сонця по еліпсах, а Сонце знаходиться в одному з фокусів цих

Слайд 17Головний наслідок з першого закону Кеплера:
відстань між планетою та Сонцем

не залишається сталою і змінюється у межах rmax≥ r

≥ rmin .

Головний наслідок з першого закону Кеплера:відстань між планетою та Сонцем не залишається сталою і змінюється у межах

Слайд 18Точка А орбіти, де планета підлітає найближче до Сонця, називається

перигелієм (від грец. peri — поблизу, helios — Сонце), а

точка, де планета знаходиться на найбільшій відстані від Сонця (точка В), — афелієм (від грец. аро — вдалині).

Точка А орбіти, де планета підлітає найближче до Сонця, називається перигелієм (від грец. peri — поблизу, helios

Слайд 19Сума відстаней від планети до Сонця в перигелії і афелії

дорівнює великій осі АВ еліпса: rmax+ rmin = 2a.

Велика піввісь земної орбіти (ОА або OB) називається астрономічною одиницею,
а = 1 а. о. = 149,6 • 106 км.

Сума відстаней від планети до Сонця в перигелії і афелії дорівнює великій осі АВ еліпса: rmax+

Слайд 20Земля в перигелії З—4 січня на найменшій відстані від Сонця

— 147 млн. км

Земля в афелії 4 липня найдальше від

Сонця — 152 млн. км

Земля в перигелії З—4 січня на найменшій відстані від Сонця — 147 млн. кмЗемля в афелії 4

Слайд 21Супутники планет теж рухаються по еліптичних орбітах, причому у фокусі

кожної орбіти знаходиться центр відповідної планети.

Слайд 22Другий закон Кеплера:
Радіус-вектор планети за рівні проміжки часу описує рівні

площі.

Слайд 23Головний наслідок другого закону Кеплера:
при рухові планети по орбіті

з часом змінюється не тільки відстань планети від Сонця, але

і її лінійна швидкість.

Головний наслідок другого закону Кеплера: при рухові планети по орбіті з часом змінюється не тільки відстань планети

Слайд 24Найбільшу швидкість планета має в перигелії, коли відстань до Сонця

найменша, а найменшу швидкість — в афелії, коли відстань найбільша.

Найбільшу

швидкість Земля має взимку:
Vmax = 30,38 км/с

Найменшу швидкість Земля має влітку:
V min= 29,36 км/с

Найбільшу швидкість планета має в перигелії, коли відстань до Сонця найменша, а найменшу швидкість — в афелії,

Слайд 25Третій закон Keплера:
Квадрати сидеричних періодів обертання планет навколо Сонця співвідносяться

як куби великих півосей їх орбіт:

Слайд 26Великий англійський фізик та математик Ісаак Ньютон довів, що закони

Кеплера не досить точно описують рух планет навколо Сонця, бо

у Всесвіті існує фундаментальний закон всесвітнього тяжіння, який не тільки зумовлює рух планет у Сонячній системі, але й визначає взаємодію зір у Галактиці.

Великий англійський фізик та математик Ісаак Ньютон довів, що закони Кеплера не досить точно описують рух планет

Слайд 27Закон всесвітнього тяжіння
У 1687 р. І. Ньютон сформулював цей

закон так:
дві матеріальні точки притягуються одна до одної з

силою, величина якої пропорційна добуткові їх мас та обернено пропорційна квадрату відстані між ними

Закон всесвітнього тяжіння У 1687 р. І. Ньютон сформулював цей закон так: дві матеріальні точки притягуються одна

Слайд 28У реальних умовах жодна планета не рухається по еліптичній траєкторії,

бо закони Кеплера справедливі тільки для двох тіл, які обертаються

навколо спільного центра мас. Відомо, що у Сонячній системі обертаються навколо Сонця 9 великих планет та безліч малих тіл, тому кожну планету притягує не тільки Сонце — одночасно притягаються між собою всі ці тіла. У результаті такої взаємодії різних за величиною і напрямком сил рух кожної планети стає досить складним, і його називають збуреним. Орбіта, по якій рухається при збуреному русі планета, не буде еліпсом.