Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в живой природе
Содержание
- 1. Симметрия в живой природе
- 2. Симметрия СИММЕТРИЯ, в геометрии — свойство геометрических
- 3. Основные понятия теории симметрииКакие тела обычно считают
- 4. Двусторонняя симметрияПод отражениями понимают любые зеркальные отражения
- 5. Нульмерная симметрияНульмерная симметрия, присуща телам, бесконечно вытянутым
- 6. Одномерная симметрияОдномерная симметрия присуща телам, во-первых, вытянутым
- 7. Двумерная симметрияДвумерной симметрией обладают тела, во-первых, вытянутые
- 8. Трехмерная симметрия Трехмерная симметрия присуща
- 9. Дисимметрические объектыОбъекты, симметрия которых исчерпывается лишь простыми
- 10. Формы дисимметрических объектовДисимметрические объекты могут существовать в
- 11. Биологическая изомерияСамое главное достижение — создание теории
- 12. Частота встреч П- и Л-формы биообъектов. Как
- 13. Свойства П- и Л-форм.
- 14. Причина свойств П- и Л-формНикакой теории, отвечающей
- 15. Интересный факт Много интересных фактов
- 16. Заключение Конечно, смена видов симметрии по мере
- 17. Содержание Титульный листСимметрия Основные понятия теории симметрии
- 18. Скачать презентанцию
Симметрия СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно
Слайды и текст этой презентации
Слайд 1«Симметрия в живой природе»
Подготовила ученица 10 «А» класса Волгоградской Гимназии
№1 Дубоносовой Анны
Слайд 2Симметрия
СИММЕТРИЯ, в геометрии — свойство геометрических фигур. Две точки,
лежащие на одном перпендикуляре к данной плоскости (или прямой) по
разные стороны и на одинаковом расстоянии от нее, называются симметричными относительно этой плоскости (или прямой). Фигура (плоская или пространственная) симметрична относительно прямой (оси симметрии) или плоскости (плоскости симметрии), если ее точки попарно обладают указанным свойством. Фигура симметрична относительно точки (центр симметрии), если ее точки попарно лежат на прямых, проходящих через центр симметрии, по разные стороны и на равных расстояниях от него.Слайд 3Основные понятия теории симметрии
Какие тела обычно считают равными? Такие, которые
при взаимном наложении совмещаются друг с другом во всех своих
деталях, как, например, два лепестка на рисунке а. Однако в теории симметрии помимо такого совместимого равенства выделяют еще два вида равенства — зеркальное и совместимо-зеркальное. При зеркальном равенстве левый лепесток рисунка б, можно точно совместить с правым лепестком, лишь отразив его предварительно в зеркале. Если же два тела можно совместить друг с другом как до, так и после отражения в зеркале, это совместимо-зеркальное равенство. Лепестки на рисунке , в равны друг другу и совместимо и зеркально. Но наличия одних равных частей в фигуре еще недостаточно, чтобы признать фигуру симметричной: на рисунке , г лепестки венчика цветка расположены хаотично, незакономерно и фигура несимметрична, внизу д лепестки расположены однообразно, закономерно и венчик симметричен. Такое закономерное, однообразное расположение равных частей фигуры относительно друг друга и называют симметрией.Слайд 4Двусторонняя симметрия
Под отражениями понимают любые зеркальные отражения — в точке,
линии, плоскости. Воображаемая плоскость, которая делит фигуры на две зеркальные
половины, называется плоскостью симметрии. Каждая из изображенных на рисунке фигур — рак, бабочка, лист растения — обладает лишь одной плоскостью симметрии, делящей ее на две зеркально равные части. Поэтому данный вид симметрии в биологии называется или билатеральной.Слайд 5Нульмерная симметрия
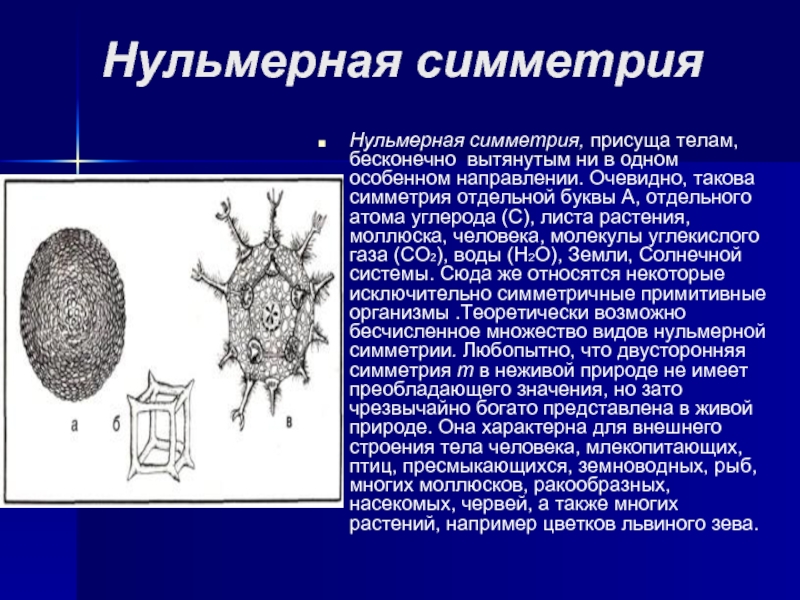
Нульмерная симметрия, присуща телам, бесконечно вытянутым ни в одном
особенном направлении. Очевидно, такова симметрия отдельной буквы А, отдельного атома
углерода (С), листа растения, моллюска, человека, молекулы углекислого газа (СО2), воды (Н2О), Земли, Солнечной системы. Сюда же относятся некоторые исключительно симметричные примитивные организмы .Теоретически возможно бесчисленное множество видов нульмерной симметрии. Любопытно, что двусторонняя симметрия m в неживой природе не имеет преобладающего значения, но зато чрезвычайно богато представлена в живой природе. Она характерна для внешнего строения тела человека, млекопитающих, птиц, пресмыкающихся, земноводных, рыб, многих моллюсков, ракообразных, насекомых, червей, а также многих растений, например цветков львиного зева.Слайд 6Одномерная симметрия
Одномерная симметрия присуща телам, во-первых, вытянутым в одном каком-либо
особенном направлении, во-вторых, вытянутым в этом направлении благодаря монотонному повторению
— «размножению» одной и той же части. Из биологических объектов такую симметрию имеют наиболее важные для обмена веществ полимерные цепные молекулы белков, нуклеиновых кислот, целлюлозы, крахмала; вирусы табачной мозаики, побеги традесканции, отрезки тела полихет и многих других животныхСлайд 7Двумерная симметрия
Двумерной симметрией обладают тела, во-первых, вытянутые в двух взаимно
перпендикулярных направлениях, во-вторых, вытянутые в этих направлениях благодаря «размножению» одной
и той же части. Такова, например, симметрия бесконечного шахматного поля, построенного бесконечным повторением черного и белого квадратиков в двух направлениях, перпендикулярных друг другу. Из биологических объектов такую симметрию имеют плоские орнаменты граней кристаллов ферментов, чешуи рыб, клеток в биологических срезах, мозаичного взаиморасположения листьев, «электронных картин» поперечного среза мышечной фибриллы, однородных сообществ организмов, складчатых слоев полипептидных цепей.Слайд 8Трехмерная симметрия
Трехмерная симметрия присуща телам, во-первых, вытянутым
в трех взаимно перпендикулярных направлениях, во-вторых, вытянутым в этих трех
направлениях благодаря монотонному повторению одной и той же части. Такова симметрия биологических кристаллов, построенных «бесконечным» повторением одних и тех же кристаллических ячеек — в длину, ширину и высотуСлайд 9Дисимметрические объекты
Объекты, симметрия которых исчерпывается лишь простыми (круговыми), или (и)
переносными (трансляционными), или (и) винтовыми осями симметрии, называются дисимметрическими, т.
е. расстроенной симметрии. К таким объектам относятся и тела аксиальной симметрии. От всех остальных объектов дисимметрические отличаются, в частности, очень своеобразным отношением к зеркальному отражению. Если тело речного рака после зеркального отражения совсем не изменяет своей формы, то аксиальный цветок анютиных глазок), асимметрическая винтовая раковина моллюска, кристалл кварца, асимметрическая молекула после зеркального отражения изменяют свою фигуру, приобретая ряд противоположных признаков. Так, винтовая раковина брюхоногого моллюска, расположенного перед зеркалом, закручена слева вверх направо, а зеркального — справа вверх налево и т. д.Слайд 10Формы дисимметрических объектов
Дисимметрические объекты могут существовать в двух разновидностях: в
виде оригинала и зеркального отражения (руки человека, раковины моллюсков, венчики
анютиных глазок, кристаллы кварца). При этом одна из форм (неважно какая) называется правой — П, а другая левой — Л. Здесь очень важно уяснить себе, что правыми и левыми называются не только руки или ноги человека, но и любые дисимметрические тела — винты с правой и левой резьбой, организмы, неживые тела. Обнаружение и в живой природе П- и Л-форм поставило перед биологией ряд новых и очень важных вопросов, многие из которых сейчас решаются сложными математическими и физико-химическими методами.Слайд 11Биологическая изомерия
Самое главное достижение — создание теории строения П- и
Л-биообъектов. На ее основе было предсказано много совершенно новых типов
и классов изомерии, предсказана и открыта советскими учеными биологическая изомерия. Изомерия — это множество объектов различного строения, но при одном и том же наборе составляющих эти объекты частей. На рисунке показана изомерия венчиков, предсказанная, а затем и обнаруженная на многих десятках тысяч экземпляров венчиков цветков около 60 видов растений. Здесь для каждого случая число лепестков одно и то же — 5, различно лишь их взаимное расположение.Слайд 12Частота встреч П- и Л-формы биообъектов.
Как часто встречаются
П- и Л-формы биообъектов? Найдено, что частота встречаемости этих форм
(Е) подчиняется следующей общей для всей живой природы закономерности: либо ЕП = ЕЛ, либо ЕП > ЕЛ, либо ЕП < ЕЛ форм — соответственно для одних, других, третьих биообъектов. Например, ЕH форм листьев бегонии и традесканции равна ЕЛ их форм. Нарцисс, ячмень, рогоз и многие другие растения — правши: их листья встречаются только в П-винтовой форме. Зато фасоль — левша, листья первого яруса до 2,3 раза чаще бывают Л-формы. Задняя часть тела волков и собак при беге несколько заносится вбок, поэтому их разделяют на право- и левобегающих. Птицы-левши складывают крылья так, что левое крыло накладывается на правое, а правши — наоборот. Некоторые голуби при полете предпочитают кружиться вправо, а другие — влево. За это голубей издавна в народе делят на «правухов» и «левухов». Раковина моллюска фрутицикола лантци встречается главным образом в П-закрученной форме. Замечено, что при питании морковью преобладающие П-формы этого моллюска прекрасно растут, а их антиподы — Л-моллюски резко теряют в весе. Инфузория-туфелька из-за спирального расположения ресничек на ее теле передвигается в капельке воды, как и многие другие простейшие, по левозавивающемуся штопору. Инфузории, вбуравливающиеся в среду по правому штопору, встречаются редко.Слайд 13Свойства П- и Л-форм.
Основное достижение —
это открытие дисимметрии жизни (СССР). Оказывается, ряд свойств П- и
Л-форм биообъектов качественно различаются. Вот некоторые примеры. Широкоизвестный антибиотик пенициллин вырабатывается грибком только в П-форме; искусственно приготовленная Л-форма его антибиотически неактивна. В аптеках продается антибиотик левомицетин, а не его антипод — правомицетин, так как последний по своим лечебным свойствам значительно уступает первому. В табаке содержится алкалоид Л-никотин. Он в несколько раз более ядовит, чем искусственно приготовленный П-никотин. Чаще встречающиеся винтообразные Л-корнеплоды сахарной свеклы содержат на 0,5— 1 % больше сахара, чем П-корнеплоды. Чаще встречающиеся (на 2—3%) левовинтовые по расположению листьев кокосовые пальмы более урожайны (в среднем на 12%), чем П-пальмы. Семена Л-растений подсолнечника более масличны (на 1,4%), чем семена П-растений. Коробочки льна, полученные с различных по изомерии венчиков цветков, различаются и количественно и качественно по содержанию жирных кислот.Слайд 14Причина свойств П- и Л-форм
Никакой теории, отвечающей на этот вопрос,
пока не существует. Предложенные гипотезы исходят из молекулярно-химической обусловленности П-
и Л-модификаций организмов и их органов. В частности, было установлено, что, выращивая микроорганизмы бациллюс микоидес на агар-агаре с П- и Л-соединениями (сахарозой, винной кислотой, аминокислотами), Л-формы его можно превратить в П-формы, а П-формы в Л-формы. В ряде случаев эти изменения носили длительный, возможно, наследственный характер. Эти опыты говорят о том, что внешняя П- или Л-форма организмов зависит от обмена веществ и участвующих в этом обмене П- и Л-молекул.Слайд 15Интересный факт
Много интересных фактов может сообщить наука
о симметрии и о человеке. Как известно, в среднем на
земном шаре примерно 3 % левшей (99 млн.) и 97 % правшей (3 млрд. 201 млн.). Интересно отметить, что центры речи в головном мозгу у правшей расположены слева, а у левшей — справа (по другим данным — в обоих полушариях). Правая половина тела управляется левым, а левая — правым полушарием, и в большинстве случаев правая половина тела и левое полушарие развиты лучше. У людей, как известно, сердце на левой стороне, печень — на правой. Но на каждые 7—12 тыс. человек встречаются люди, у которых все или часть внутренних органов расположены зеркально, т. е. наоборот. Но самое важное в этой области открытие было сделано на молекулярно-химическом уровне. Знаменитый французский ученый Л. Пастер и многие другие ученые обнаружили, что клетки организмов состоят в основном только или преимущественно из Л-аминокислот, Л-белков, П-нуклеиновых кислот, П-сахаров, Л-алкалоидов. Такую особенность протоплазмы Пастер назвал дисимметрией протоплазмы.Слайд 16Заключение
Конечно, смена видов симметрии по мере эволюции жизни происходила
не только у дисимметрических организмов. Так, некоторые иглокожие когда-то были
двустороннесимметричными подвижными формами. Затем они перешли к сидячему образу жизни, и у них выработалась радиальная симметрия (правда, личинки их до сих пор сохранили двустороннюю симметрию). У части иглокожих, вторично перешедших к активному образу жизни, радиальная симметрия вновь заменилась билатеральной (неправильные ежи, голотурии).Слайд 17Содержание
Титульный лист
Симметрия
Основные понятия теории симметрии
Двусторонняя симметрия
Нульмерная симметрия
Одномерная
симметрия
Двумерная симметрия
Трехмерная симметрия
Дисимметрические объекты
Формы дисимметрических объектов
Биологическая изомерия
Частота встреч П- и
Л-формы биообъектов.Свойства П- и Л-форм
Причина свойств П- и Л-форм
Интересный факт
Заключение
Теги