Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Свободные колебания. Колебательные системы.
Содержание
- 1. Свободные колебания. Колебательные системы.
- 2. Свободные колебания (или собственные колебания) — это колебания колебательной
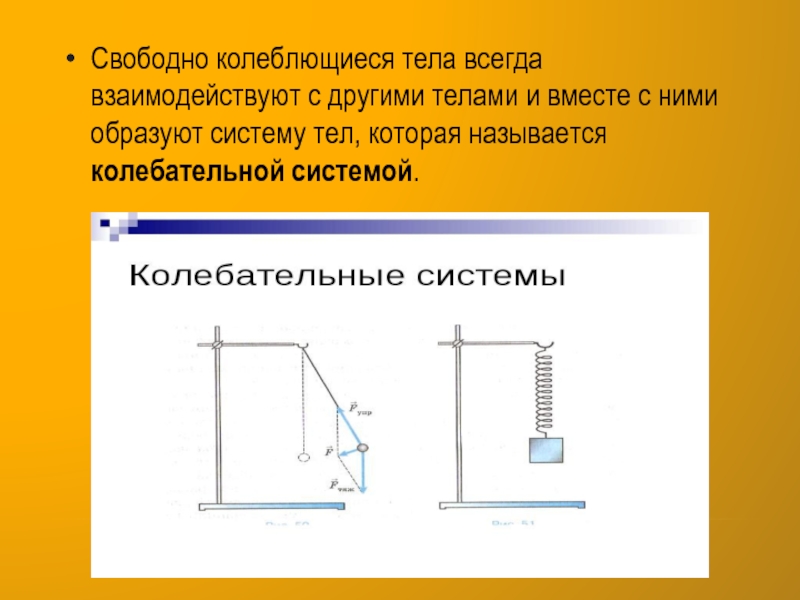
- 3. Свободно колеблющиеся тела всегда взаимодействуют с другими
- 4. Например, пружина, шарик и вертикальная стойка, к
- 5. Другим классическим примером механической колебательной системы является математический маятник.
- 6. В физике различают несколько типов маятников нитяные,
- 7. Ну а пружинные маятники состоят из тела и некой пружины, которая и обусловливает колебания.
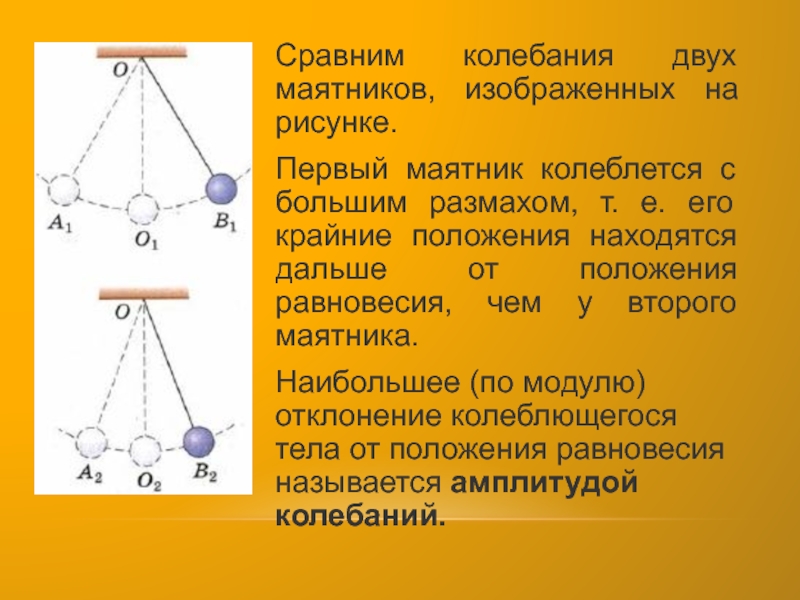
- 8. Сравним колебания двух маятников, изображенных на рисунке.Первый
- 9. Колеблющееся тело совершает одно полное колебание, если
- 10. Подвесим два одинаковых шарика на нитях разной
- 11. Обозначается частота греческой буквой v («ню»). За
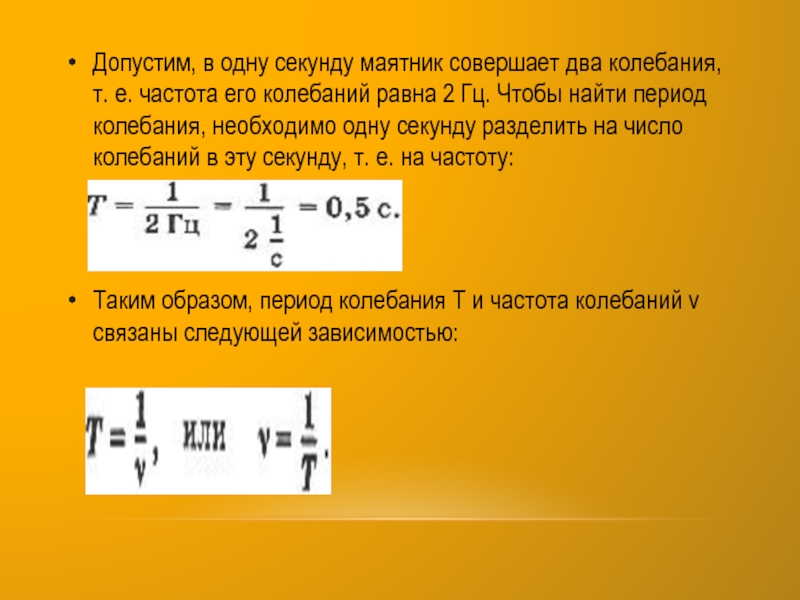
- 12. Допустим, в одну секунду маятник совершает два
- 13. На примере колебаний маятников разной длины приходим
- 14. Не только нитяной маятник, но и любая
- 15. Рассмотрим колебания двух одинаковых маятников. В один
- 16. Маятники, изображенные на рисунке, тоже колеблются с
- 17. Физическая величина, называемая фазой, используется не только
- 18. Итоги урокаКолебательные системы-это-….Амплитуда колебаний-это…, обозначается…., измеряется…Периодом колебаний
- 19. Домашнее задание:§24-25
- 20. Скачать презентанцию
Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии при отсутствии внешних воздействий.
Слайды и текст этой презентации
Слайд 1Свободные колебания. Колебательные системы. Маятник.
Величины, характеризующие колебательное движение.
Слайд 2Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только
благодаря первоначально сообщенной энергии при отсутствии внешних воздействий.
Слайд 3Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе
с ними образуют систему тел, которая называется колебательной системой.
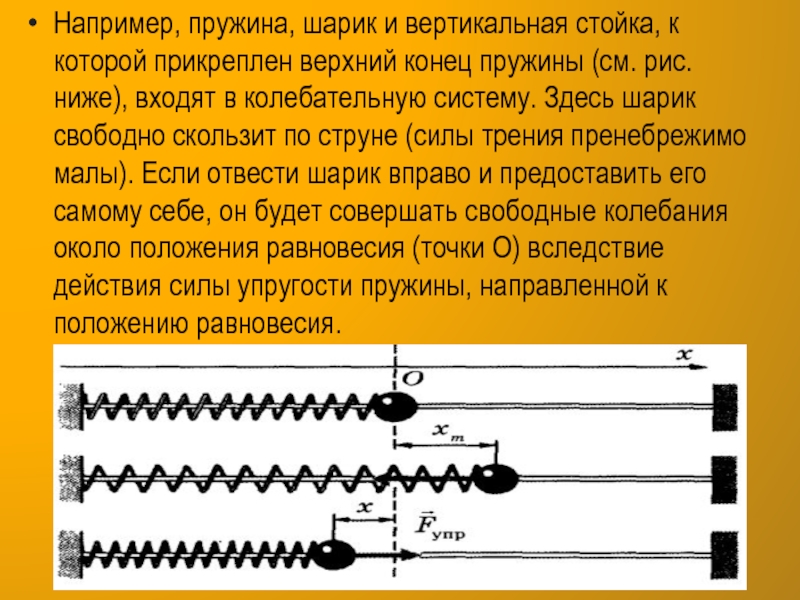
Слайд 4Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний
конец пружины (см. рис. ниже), входят в колебательную систему. Здесь
шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.Слайд 5Другим классическим примером механической колебательной системы является математический маятник.
Слайд 6В физике различают несколько типов маятников нитяные, пружинные и некоторые
другие. Все системы, в которых колеблющееся тело или его подвес
можно условно представить в виде нити, являются нитяными.Слайд 8Сравним колебания двух маятников, изображенных на рисунке.
Первый маятник колеблется с
большим размахом, т. е. его крайние положения находятся дальше от
положения равновесия, чем у второго маятника.Наибольшее (по модулю) отклонение колеблющегося тела от положения равновесия называется амплитудой колебаний.
Слайд 9Колеблющееся тело совершает одно полное колебание, если от начала колебаний
проходит путь, равный четырём амплитудам. Например, переместившись из точки О1
в точку B1 затем в точку А1 и вновь в точку О1 (шарик совершает одно полное колебание).Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обозначается буквой Т и в СИ измеряется в секундах (с).
Слайд 10Подвесим два одинаковых шарика на нитях разной длины и приведём
их в колебательное движение. Увидим, что за один и тот
же промежуток времени короткий маятник совершит больше колебаний, чем длинный.Число колебаний в единицу времени называется частотой колебаний.
Слайд 11Обозначается частота греческой буквой v («ню»). За единицу частоты принято
одно колебание в секунду. Эта единица в честь немецкого учёного
Генриха Герца названа герцем (Гц).Слайд 12Допустим, в одну секунду маятник совершает два колебания, т. е.
частота его колебаний равна 2 Гц. Чтобы найти период колебания,
необходимо одну секунду разделить на число колебаний в эту секунду, т. е. на частоту:Таким образом, период колебания Т и частота колебаний v связаны следующей зависимостью:
Слайд 13На примере колебаний маятников разной длины приходим к выводу: частота
и период свободных колебаний нитяного маятника зависят от длины его
нити. Чем больше длина нити маятника, тем больше период колебаний и меньше частота.Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы
Слайд 14Не только нитяной маятник, но и любая другая колебательная система
имеет определённую собственную частоту, зависящую от параметров этой системы. Например,
собственная частота пружинного маятника зависит от массы груза и жёсткости пружины.Слайд 15Рассмотрим колебания двух одинаковых маятников. В один и тот же
момент времени левый маятник из крайнего левого положения начинает движение
вправо, а правый маятник из крайнего правого положения движется влево. Оба маятника колеблются с одной и той же частотой (поскольку длины их нитей равны) и с одинаковыми амплитудами. Однако эти колебания отличаются друг от друга: в любой момент времени скорости маятников направлены в противоположные стороны. В таком случае говорят, что колебания маятников происходят в противоположных фазах.Слайд 16Маятники, изображенные на рисунке, тоже колеблются с одинаковыми частотами. Скорости
этих маятников в любой момент времени направлены одинаково. В этом
случае говорят, что маятники колеблются в одинаковых фазах.Рассмотрим ещё один случай. В момент, изображённый на рисунке а, скорости обоих маятников направлены вправо. Но через некоторое время, рисунок б, они будут направлены в разные стороны. В таком случае говорят, что колебания происходят с определённой разностью фаз.
Слайд 17Физическая величина, называемая фазой, используется не только при сравнении колебаний
двух или нескольких тел, но и для описания колебаний одного
тела.Таким образом, колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой.
Слайд 18Итоги урока
Колебательные системы-это-….
Амплитуда колебаний-это…, обозначается…., измеряется…
Периодом колебаний называется…, обозначается…, измеряется…
Частотой
называется…, обозначается…, измеряется…
Между периодом и частотой существует математическая зависимость, которая
записывается формулой…Если маятники колеблется в одинаковых фазах то скорости этих маятникв по направлению…