Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Базовой курс информатики
Содержание
- 1. Базовой курс информатики
- 2. ФОРМЫ МЫШЛЕНИЯПОНЯТИЕ ЛОГИЧЕСКИХ ПЕРЕМЕННЫХЛОГИЧЕСКИЕ ОПЕРАЦИИЛОГИЧЕСКИЕ ФУНКЦИИЗАКОНЫ ЛОГИКИЗАДАЧИЗАКЛЮЧЕНИЕЛОГИЧЕСКИЕОСНОВЫ ПКИЗ ИСТОРИИ ТЕМЫ ОБ АВТОРЕВЫХОД
- 3. ЛОГИКА — наука, изучающая законы и формы
- 4. ПРИМЕРЫ ВЫСКАЗЫВАНИЙ:Земля- планета солнечной системы.5 × 5
- 5. Примеры суждений: 1. Р – простое число 2. Х +
- 6. В приведенных предложениях выделите высказывания:Москва расположена между
- 7. КВАНТОРЫ Выражение «для всякого х» в логике
- 8. Пример: Х – «На столе лежит ручка»
- 9. Пример: Х – «В библиотеке можно взять
- 10. Пример: Х – «В библиотеке можно взять
- 11. Эта операция обозначается символами «• »
- 12. Х – условие (посылка) Y– заключение (следствие)Пример:Х
- 13. Пример: Х – «Компьютер может производить вычисления»Y
- 14. Порядок выполнения операцийИнверсияКонъюнкцияДизъюнкция, строгая дизъюнкцияИмпликацияЭквивалентностьДля изменения указанного порядка используются круглые скобки.ЛОГИЧЕСКИЕ ОПЕРАЦИИ
- 15. Дайте название каждой логической операции: а) Если две
- 16. Для каждой из приведенных формул придумайте по
- 17. ЛОГИЧЕСКИЕ ФУНКЦИИ Любое составное высказывание можно рассматривать как
- 18. ЗАКОНЫ ЛОГИКИ Формула имеет нормальную форму, если в
- 19. ЗАКОНЫ ЛОГИКИ10) закон поглощения: А∧(А∨В) =А А∨(А∧В)
- 20. В соответствии с законами логики определите результаты
- 21. ДЛЯ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ НУЖНО:Внимательно изучить условие.Выделить
- 22. Найдите значения логических выражений: а) (1∨1)∨(1∨0)=1 ∨1=1; б) ((1∨0)∨1)∨1; в)
- 23. Выполните поразрядное логическое сложение двоичных чисел а) 100
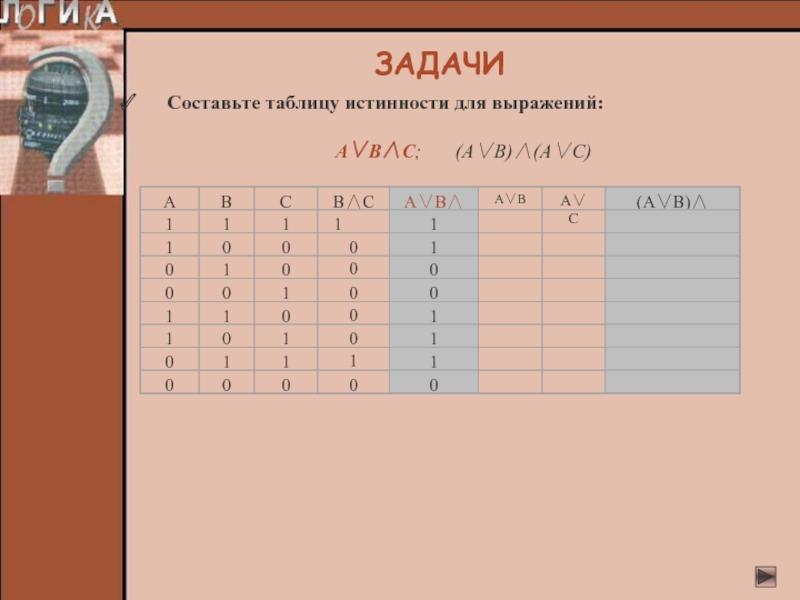
- 24. Составьте таблицу истинности для выражений: А∨В∧С; (А∨В)∧(А∨С)ЗАДАЧИ
- 25. Даны два сложных высказывания: а) если одно
- 26. Даны два сложных высказывания: а) если
- 27. Каждую из приведенных формул упростите так, чтобы
- 28. Определите, кто из подозреваемых участвовал в преступлении,
- 29. ЗАДАЧИАня, Вика и Сергей решили пойти в
- 30. К помощи логики человек прибегает очень часто:
- 31. Учитель информатики и ИКТ МОУ Черкасской средней школыПясецкая Анна Андреевна
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
ФОРМЫ МЫШЛЕНИЯ
ПОНЯТИЕ ЛОГИЧЕСКИХ ПЕРЕМЕННЫХ
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
ЛОГИЧЕСКИЕ ФУНКЦИИ
ЗАКОНЫ ЛОГИКИ
ЗАДАЧИ
ЗАКЛЮЧЕНИЕ
ЛОГИЧЕСКИЕ
ОСНОВЫ ПК
ИЗ ИСТОРИИ
ТЕМЫ
ОБ АВТОРЕ
ВЫХОД
Слайд 3ЛОГИКА — наука, изучающая законы и формы мышления; учение о
способах рассуждений и доказательств.
ПОНЯТИЕ — форма мышления, в которой
отражаются существенные признаки отдельного предмета или класса однородных предметов. Понятия в языке выражаются словами. СУЖДЕНИЕ — это форма мышления, в которой что-либо утверждается или отрицается о предметах, признаках или их отношениях.
УМОЗАКЛЮЧЕНИЕ — форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, мы по определенным правилам вывода получаем суждение-заключение.
Формы мышления
Слайд 4
ПРИМЕРЫ ВЫСКАЗЫВАНИЙ:
Земля- планета солнечной системы.
5 × 5 = 25
Яблоки растут
на хвойных деревья
Вода – жидкость
2 > 3
АЛГЕБРА ЛОГИКИ
(или Булева алгебра) оперирует с ЛОГИЧЕСКИМИ ПЕРЕМЕННЫМИ – высказываниями и суждениями (предикатами)ВЫСКАЗЫВАНИЯ – это конкретные частные утверждения, о которых можно судить, истинно оно или ложно. В естественных языках высказывания выражаются повествовательными предложениями.
ПОНЯТИЕ ЛОГИЧЕСКИХ ПЕРЕМЕННЫХ
В
ы
С
К
А
З
ы
В
А
Н
И
Я
Слайд 5
Примеры суждений:
1. Р – простое число
2. Х + У > 0
3. N
– четное число
Суждения становятся высказываниями, если переменным придать числовые значения
(пример: 3 – простое число).Логические переменные могут принимать только два значения:
ИСТИННА - 1 или ЛОЖЬ – 0
СУЖДЕНИЯ (предикаты) – это утверждения о переменных.
ПОНЯТИЕ ЛОГИЧЕСКИХ ПЕРЕМЕННЫХ
С
У
ж
Д
Е
Н
И
Я
Слайд 6
В приведенных предложениях выделите высказывания:
Москва расположена между Киевом и Одессой.
Есть
ли на свете человек, который мог объять необъятное?
Я земной шар
чуть не весь обошел!Солнце есть спутник земли.
Если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный.
2+3=4
Сегодня отличная погода.
Железо – металл.
Если один угол в треугольнике прямой, то треугольник будет тупоугольным.
Который час?
Да здравствует 1 сентября!
Здесь нет высказываний.
ПОНЯТИЕ ЛОГИЧЕСКИХ ПЕРЕМЕННЫХ
Слайд 7
КВАНТОРЫ
Выражение «для всякого х» в логике называется квантором всеобщности по
переменной х
КВАНТОР ВСЕОБЩНОСТИ ∀ (все, всякий, каждый ).
Пример: Все следователи
– юристы. Все кошки являются рыбами.ИСТИННОСТЬ ВЫСКАЗЫВАНИЯ С КВАНТОРОМ ОБЩНОСТИ УСТАНАВЛИВАЕТСЯ ПУТЕМ ДОКАЗАТЕЛЬСТВА, А ПОКАЗАТЬ ЛОЖНОСТЬ МОЖНО, ПРИВЕДЯ КОНТРПРИМЕР.
Выражение «существует х такое, что …» в логике называется квантором существования по переменной х
КВАНТОР СУЩЕСТВОВАНИЯ ∃(некоторые, существуют).
Пример: Некоторые следователи имеют высшее образование. Некоторые студенты – отличники.
ИСТИННОСТЬ ВЫСКАЗЫВАНИЯ С КВАНТОРОМ СУЩЕСТВОВАНИЯ УСТАНАВЛИВАЕТСЯ ПРИ ПОМОЩИ КОНТРЕКТНОГО ПРИМЕРА, А ЧТОБЫ УБЕДИТЬСЯ В ЛОЖНОСТИ НЕОБХОДИМО ПРОВЕСТИ ДОКАЗАТЕЛЬСТВО.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
К
В
А
Н
Т
О
Р
ы
Слайд 8Пример: Х – «На столе лежит ручка»
Y – «На столе лежит карандаш»
Х∧Y – «На столе лежит
ручка и на столе лежит карандаш»
Эта операция обозначается символами «∧» или «&».
В программировании эту операцию обозначают «AND».
КОНЪЮНКЦИЯ
Таблица истинности
Соединение двух логических переменных с помощью союза
«И» называется логическим умножением или КОНЪЮНКЦИЕЙ
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
К
О
Н
Ъ
ю
Н
К
Ц
И
Я
Слайд 9
Пример: Х – «В библиотеке можно взять книгу»
Y – «В
библиотеке можно просмотреть журнал»
Х∨Y – «В библиотеке можно взять книгу
или в библиотеке можно просмотреть журнал»
ДИЗЪЮНКЦИЯ
Эта операция обозначается символами «∨» или «+».
В программировании эту операцию обозначают «OR».
Таблица истинности
Соединение двух логических переменных с помощью союза
«ИЛИ» называется логическим сложением или ДИЗЪЮНКЦИЕЙ.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Д
И
З
Ъ
ю
Н
К
Ц
И
Я
Слайд 10
Пример: Х – «В библиотеке можно взять книгу»
Y – «В
библиотеке можно просмотреть журнал»
Х⊕Y – «В библиотеке можно взять либо
книгу, либо в библиотеке можно просмотреть журнал»
СТРОГАЯ ДИЗЪЮНКЦИЯ
Эта операция обозначается символами «∨» или «⊕».
В программировании эту операцию обозначают «ХOR».
Таблица истинности
Соединение двух логических переменных с помощью союза
«ЛИБО…ЛИБО» называется ИСКЛЮЧАЮЩИМ ИЛИ или СТРОГОЙ ДИЗЪЮНКЦИЕЙ.
.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
С
Т
Р
О
Г
А
Я
Д
И
З
Ъ
ю
Н
К
Ц
И
Я
Слайд 11Эта операция обозначается символами «• » или «¬».
В
программировании эту операцию обозначают «NOT».
Пример: Х – «Точка О является центром круга»
Инверсия: «Точка О не является центром круга»
Таблица истинности
ИНВЕРСИЯ
Присоединение частицы НЕ к логической переменной называется логическим отрицанием или ИНВЕРСИЕЙ.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
И
Н
В
Е
Р
С
И
Я
Слайд 12
Х – условие (посылка) Y– заключение (следствие)
Пример:Х – «Треугольник равносторонний»
Y – «Треугольник равноугольный»
Х⇒Y – «Если треугольник равносторонний,
то он равноугольный»
Таблица истинности
ИМПЛИКАЦИЯ
Эта операция обозначается символами «→» или «⊃».
В программировании саму логическую операцию обозначают «IMP»,
а союз «если…,то…» заменяют связкой «IF…THEN…».
Соединение двух логических переменных с помощью союза «ЕСЛИ…, ТО…» называется логическим следованием или ИМПЛИКАЦИЕЙ.
«Из лжи – все, что угодно».
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
И
М
П
Л
И
К
А
Ц
И
Я
Слайд 13
Пример: Х – «Компьютер может производить вычисления»
Y – «Компьютер включен»
Эквивалентность:
««Компьютер может производить вычисления тогда и только тогда, когда компьютер
включен»ЭКВИВАЛЕНТНОСТЬ
Соединение двух логических переменных с помощью союза «…ТОГДА И ТОЛЬКО ТОГДА, КОГДА» называется логическим равенством или ЭКВИВАЛЕНТНОСТЬЮ.
Эта операция обозначается символами «≡» или «↔». В программировании саму логическую операцию обозначают «EQV».
Таблица истинности
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Э
К
В
И
В
А
Л
Е
Н
Т
Н
О
С
Т
Ь
Слайд 14Порядок выполнения операций
Инверсия
Конъюнкция
Дизъюнкция, строгая дизъюнкция
Импликация
Эквивалентность
Для изменения указанного порядка используются круглые
скобки.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Слайд 15
Дайте название каждой логической операции:
а) Если две прямые параллельны, то
они пересекаются.
б) Произведение равно нулю тогда и только тогда когда
один из множителей равен нулю.в) Завтра я не пойду в школу.
г) Зимой мы обычно ходим на лыжах или катаемся на коньках на нашем пруду.
д) Я сделал домашнюю работу и получил за нее «пять».
е) Принтер либо устройство вывода информации, либо устройство хранения информации.
2. Постройте отрицания приведенных ниже высказываний:
а) водитель автомобиля не имеет права ехать на красный свет;
б) существует параллелограмм с прямым углом;
в) любое простое число нечетно;
г) на улице сухо;
д) в школу поставили новые компьютеры.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Слайд 16
Для каждой из приведенных формул придумайте по два высказывания:
а) (А∧В)⇒С б)
•В∨С в) (В∧С)∨•А
Определите вид сложного высказывания, записав его структурной формулой
а) ни
сна, ни отдыха измученной душе; б) что неясно представляешь, то неясно и высказываешь;
в) зимой мы поедем в деревню или остановимся в городе;
г) прямо – ближе, обдуманно – быстрее.
ЛОГИЧЕСКИЕ ОПЕРАЦИИ
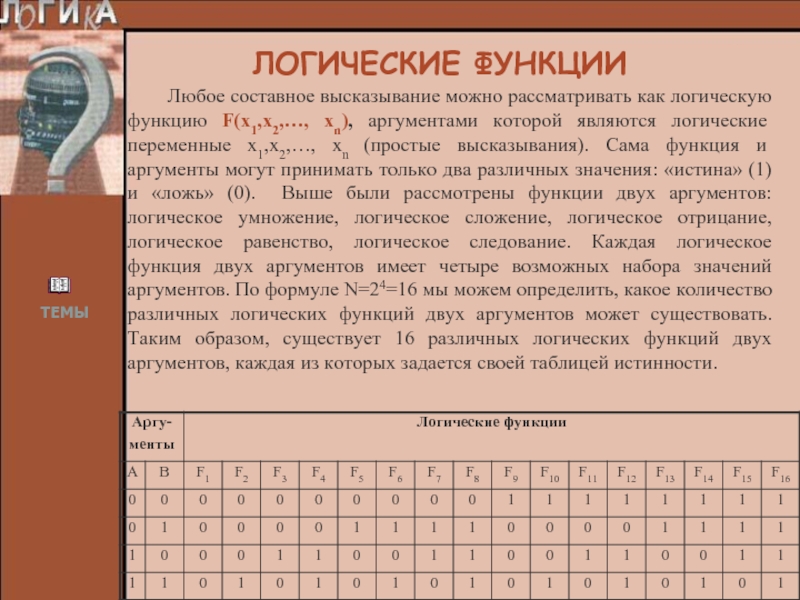
Слайд 17ЛОГИЧЕСКИЕ ФУНКЦИИ
Любое составное высказывание можно рассматривать как логическую функцию F(x1,x2,…,
xn), аргументами которой являются логические переменные x1,x2,…, xn (простые высказывания).
Сама функция и аргументы могут принимать только два различных значения: «истина» (1) и «ложь» (0). Выше были рассмотрены функции двух аргументов: логическое умножение, логическое сложение, логическое отрицание, логическое равенство, логическое следование. Каждая логическое функция двух аргументов имеет четыре возможных набора значений аргументов. По формуле N=24=16 мы можем определить, какое количество различных логических функций двух аргументов может существовать. Таким образом, существует 16 различных логических функций двух аргументов, каждая из которых задается своей таблицей истинности.Слайд 18ЗАКОНЫ ЛОГИКИ
Формула имеет нормальную форму, если в ней отсутствуют знаки
эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только
при переменных.1) закон тождества А=А
2) закон двойного отрицания (¬(¬A))=A
3) закон противоречия А ∧(¬А) = 0
4) закон исключения третьего А ∨(¬А) = 1
5) А→В= (¬А) ∨В
6) А↔В=(А ∧В) ∨((¬А) ∨ (¬В))
А↔В=((¬А) ∨ В) ∧ (А ∨ (¬В))
7) коммутативный закон: А∧В=В∧А
А∨В=В∨А
8) ассоциативный закон: ((А∧В)∧С)=(А∧(В∧С))
((А∨В) ∨С)=(А∨(В∨С))
9) дистрибутивный закон: (А∧(В∨С))=((А∧В) ∨ (А∧С))
(А∨(В∧С))=((А∨В) ∧ (А∨С))
Слайд 19ЗАКОНЫ ЛОГИКИ
10) закон поглощения: А∧(А∨В) =А
А∨(А∧В) =А
11) закон идемпотентности: А∧А=А А∨А=А
12) законы исключения констант: А∧1=А А∨1=1А∧0=0 А∨0=А
13) отрицание конъюнкций: ¬(А∧В) =(¬ А) ∨(¬ В)
14) отрицание дизъюнкций: ¬(А∨В) =(¬ А) ∧(¬ В)
15) закон исключения: (А∧В)∨((¬А)∧ В) = В
(А∨В)∧((¬А)∨В) = В
Слайд 20
В соответствии с законами логики определите результаты высказываний:
а) в соседней
комнате сейчас находится какой-то человек или неверно,
что в соседней
комнате сейчас находится какой-то человек; б) неверно, что на столе лежит ручка или на столе лежит карандаш;
в) завтра будет вьюга и будет дождь или завтра не будет вьюги и
будет дождь;
г) не является истинным, что Юра этого не делал.
ЗАКОНЫ ЛОГИКИ
Слайд 21 ДЛЯ РЕШЕНИЯ ЛОГИЧЕСКИХ ЗАДАЧ НУЖНО:
Внимательно изучить условие.
Выделить элементарные высказывания и
обозначить их –
как принято –большими латинскими буквами.
Записать условие задачи
на языке алгебры логики, соединив простые высказывания в сложные при помощи логических операций.Полученное выражение упростить, используя законы логики.
Выбрать решение – набор значений простых высказываний,
при котором выражение является истинным.
Проверить, удовлетворяет ли полученное решение условию
задачи.
ЗАДАЧИ
Слайд 22Найдите значения логических выражений:
а) (1∨1)∨(1∨0)=1 ∨1=1; б) ((1∨0)∨1)∨1;
в) (0∨1)∨(1∨0); г) (0∧1)∧1;
д) 1∧(1∧1)∧1; е)
((1∨0)∧(1∧1))∧(0∨1).
Даны два простых высказывания:
А={2·2=4}, В={2·2=5}.
Какие из составных высказываний истинны:
а) •А; б)
•В;в) А∧В; г) А∨В;
д) А⇒В; е) А⇔В?
Даны простые высказывания:
А={Принтер – устройство ввода информации}
В={Процессор – устройство обработки информации}
С={Монитор – устройство хранения информации}
D={Клавиатура – устройство ввода информации}
Определите истинность составных высказываний:
а) (А∧В)∧(С∨D); б) (А∧В)⇒(В∧С);
В) (А∨В)⇔(С∧D); г) •А⇔•В.
ЗАДАЧИ
Слайд 23Выполните поразрядное логическое сложение двоичных чисел
а) 100 и 110; б) 1010
и 1000; в) 101010 и 111111.
Даны три числа в различных системах
счисления: а) А=2010 , В=1116, С= 308.
Переведите А, В, С в двоичную систему счисления и выполните поразрядно логические операции (А∨В∧С). Ответ дайте в десятичной системе счисления.
Решение: 2010 = 101002 1116=100012 308 =110002
б) А=3010 , В=АF16, С= 568.
ЗАДАЧИ
Слайд 25
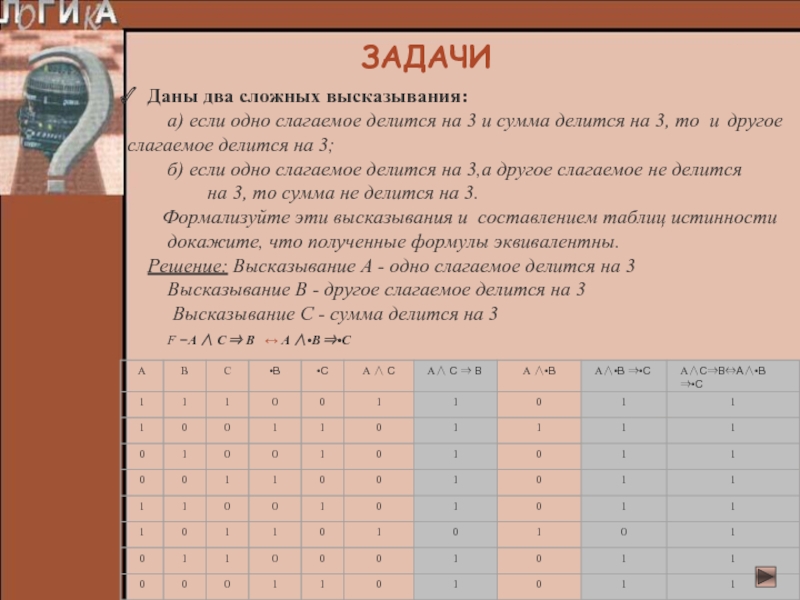
Даны два сложных высказывания:
а) если одно слагаемое делится на
3 и сумма делится на 3, то и другое слагаемое
делится на 3;б) если одно слагаемое делится на 3,а другое слагаемое не делится
на 3, то сумма не делится на 3.
Формализуйте эти высказывания и составлением таблиц истинности
докажите, что полученные формулы эквивалентны.
Решение: Высказывание А - одно слагаемое делится на 3
Высказывание В - другое слагаемое делится на 3
Высказывание С - сумма делится на 3
F =А ∧ С ⇒ В ↔ А ∧•В ⇒•С
ЗАДАЧИ
Слайд 26
Даны два сложных высказывания:
а) если a>b и (b>0
или b=0), то a>0;
б) если a>b и a>0, то b>0
или b=0.Формализуйте эти высказывания и составлением таблиц истинности
докажите, что полученные формулы эквивалентны.
Докажите с помощью таблиц истинности равносильность следующих
логических выражений:
а) (А⇒В)&(A∨•B)
б) (А⇔В)&(•A&•B)
ЗАДАЧИ
Слайд 27Каждую из приведенных формул упростите так, чтобы знак отрицания был
отнесен только к простым высказываниям:
а) ¬(A ∨ B) ∧•C =
•А∧•В ∧•C б) ¬(•А∨В)
в) ¬( A ∧•B) ∨•C
Используя законы логики упростите выражения:
а) А∨(В∧А) = А ∨(А∧В) = А
б) С∨(А∧В)∨(•А∧В)
в) A∧(A∨B)∧(A∨C)
г) (A ∧B ∧ C) ∨(A ∧ B ∧•C)
д) (А ∨•А) ∧В
ЗАДАЧИ
Слайд 28
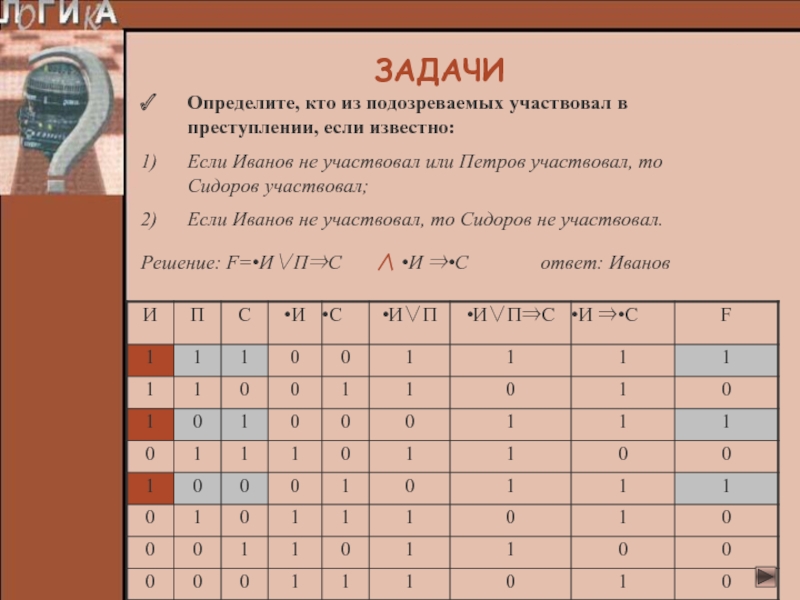
Определите, кто из подозреваемых участвовал в преступлении, если известно:
Если Иванов
не участвовал или Петров участвовал, то Сидоров участвовал;
Если Иванов не
участвовал, то Сидоров не участвовал.Решение: F=•И∨П⇒С ∧ •И ⇒•С ответ: Иванов
ЗАДАЧИ
Слайд 29
ЗАДАЧИ
Аня, Вика и Сергей решили пойти в кино. Учитель, хорошо
знавший ребят, высказал предположения:
Аня пойдет в кино только тогда, когда
пойдут Вика и Сергей;Аня и Сергей пойдут в кино вместе или же оба останутся дома;
Чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что учитель немного ошибся: из трех его утверждений истинными оказались только два. Кто из ребят пошел в кино?
В нарушении правил обмена валюты подозреваются четыре работника банка – A, B, C, D. Известно, что:
Если А нарушил, то и В нарушил правила обмена валюты.
Если В нарушил, то и С нарушил или А не нарушал.
Если D не нарушал, то А нарушил, а С не нарушал.
Если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
Слайд 30К помощи логики человек прибегает очень часто: распутывая противоречивые показания,
составляя различные расписания и во многих других случаях.
Среди задач, для
решения которых привлекается ЭВМ, немало таких, которые по традиции принято называть логическими. Кто не знает шуточной задачи о перевозке волка, козы и капусты с одного берега на другой! В такой задаче властвует не арифметика, а умение правильно рассуждать.В жизни некоторые суждения и связи между ними бывают столь противоречивыми, что такие твердые логические орешки не под силу раскусить даже вдумчивому математику. Тогда на помощь в решении таких логических задач привлекают ЭВМ. Необходимо подчеркнуть, что умение использовать логические операции (AND, OR, NOT, EQV, IMP) повышают эффективность программирования. Именно формируя условия в операторе условной передачи управления (IF…THEN), программист использует логические операции.
В основе теории создания и работы дискретных преобразователей информации (вентили, сумматоры, триггеры и т.д.) лежат аппарат алгебры логики, сведения о двоичной арифметике и теории кодирования. «Электронные мозги ошибаются гораздо точнее»
Габриэль Лауб
ЗАКЛЮЧЕНИЕ