Логические законы и правила преобразования логических выражений 8 класс

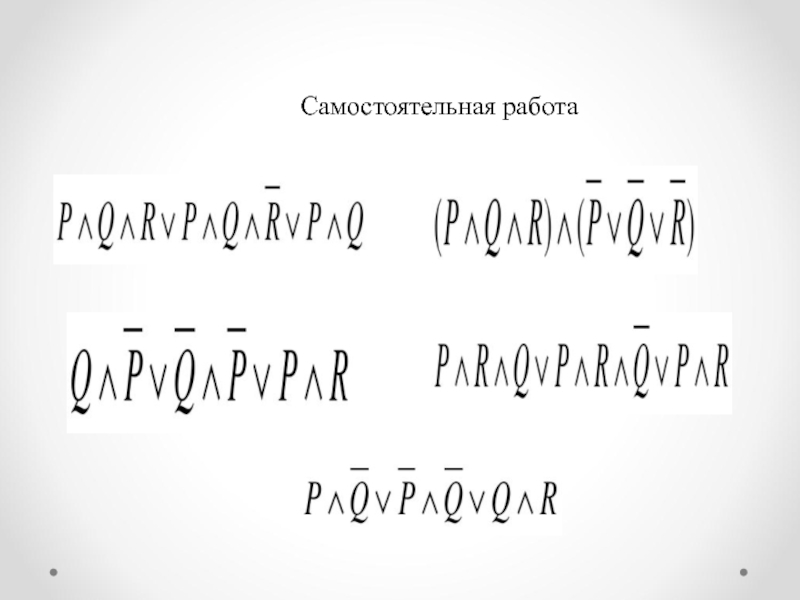
двойного отрицания
¬¬А=А

В процессе рассуждения нельзя подменять одно понятие другим
Не могут

быть одновременно истинными суждение и его отрицание
Высказывание может быть либо истинным либо ложным, третьего не дано
Если отрицать дважды некоторое суждение, то получается исходное суждение

(В ∨ С)= (А ∨ В) ∨ С
А &(В &

С)= (А & В) &С

&(A∨ С)
А & (В ∨ С)= (А & В) ∨(A&С)
Поглощение
А

∨ (А & В)=А А & (А ∨ В)=А
Законы де Моргана
¬(А ∨В)= ¬ А&¬В ¬(А &В)= ¬ А ∨ ¬В

(27.6.1806-18.3. 1871) - шотландский математик и логик. Секретарь Королевcкого астрономического

общества (1847г.), член Лондонского королевского общества. Первый президент Лондонского математического общества. Родился в Мадуре (Индия). Учился в Тринити-колледж (в Кембридже). Профессор математики в университетском колледже в Лондоне. Основные труды по алгебре, математическому анализу и математической логике. В теории рядов описал логарифмическую шкалу для критериев сходимости; занимался теорией расходящихся рядов. Один из основателей формальной алгебры. Продолжая работы Дж. Пикока, Морган в 1841-1847 гг. опубликовал ряд работ по основам алгебры. В трактате "Формальная логика или исчисление выводов необходимых и возможных" (1847г.), Морган некоторыми своими положениями опередил Дж. Буля. Позднее Морган успешно изучал логику отношений - область, не охваченную исследованиями предшественников. Написал много исторических работ, в частности книгу "Бюджет парадоксов" (1872г.). Большой вклад внес также в дедуктивную логику вообще и математическую в частности. Лондонское математическое общество учредило медаль им. О. Моргана.

= ¬ B⇒ A
Эквивалентности
А⇔В = (А&B) ∨ (¬A& ¬B)
А⇔В

= (А ∨ ¬ B) ∨ (¬A ∨ B)
А⇔В = (А ⇒ B) & (B ⇒ A)

законов алгебры высказываний с с целью получения высказываний более простой

формы

∨Z ∨ Z
C=C ∧C ∧ C
Е= ¬ ¬Е

По свойствам констант

По

закону исключения третьего
По закону непротиворечия
- По закону
идемпотентности
- По закону двойного отрицания

дистрибутивности вынесем А за скобки
А ∧ В ∨ А ∧

¬ В=

А ∧ 1=

А

А ∧(В ∨ ¬ В)=

Упростить: (А ∨ В )& (А ∨ ¬ В)

Упростить: ¬(¬ X ∨ ¬ Y )

v C).
Избавимся от импликации и отрицания. Воспользуемся

(¬(A→B)=A& ¬ B). Получится: ¬((AvB)→ ¬(BvC))= (AvB)& ¬ (¬(BvC)).
Применим закон двойного отрицания, получим: (A v В) & ¬(¬(В v С)) = (A v В) & (B v С).
Применим правило дистрибутивности ((A∙B) +(A∙C) = A∙(B+C)). Получим: (AvВ)& (B v С)= (AvB)&Bv(AvB)&C
Применим закон коммутативности (A&B=B&A ) и дистрибутивности (16). Получим: (AvB)&Bv(AvB)&C = A&BvB&BvA&CvB&C.
Применим (А& A= A) и получим: A&BvB&BvA&CvB&C= A&BvBvA&CvB&C
Применим ((A&B) v(A&C) = A&(BvC) ), т.е. вынесем за скобки В. Получим:A&BvBvA&CvB&C= B& (Av1)vA&CvB&C.
Применим (Аv 1= 1 ). Получим:B& (Av1) vA&CvB&C= BvA&CvB&C.
Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:BvA&CvB&C = B& (1vC)vA&C.
Применим (Аv 1= 1 ) и получим ответ: B&(1vC)vA&C=BvA&C.

(BvC).
F = (A→B) v (B→A).
F = A&CvĀ&C.
F =AvBvCvAvBvC
№2
Упростите выражение:
F

= ¬(X&Yv ¬(X&Y)).
F = X&¬ (YvX).
F = (XvZ) & (XvZ) & (YvZ).

X&¬ (YvX) = X&Y.
F = (XvZ) & (XvZ) & (YvZ)

=X&(YvZ).

Ответы к № 1:
F = ¬ (A&B) v ¬ (BvC) =AvB.
F= (A→B) v (B→A) = 1.
F = A&CvĀ&C=C.
F =AvBvCvAvBvC=1.

не Y))
F= B&(AvA&B)
0&Xv0
F= не Х или (не (Х и Yи

не Y))
F= (AvC)&(AvC)&(BvC)
0vX&1
F= не Х и (не(неY или Х))
F=A&B v A&Bv A&BvB&C