Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики
Содержание
- 1. Основы логики
- 2. ЛОГИКА -- ЭТО УЧЕНИЕ О СПОСОБАХ РАССУЖДЕНИЙ
- 3. РАЗВИТИЕ ЛОГИКИ: СОКРАТПЛАТОНАРИСТОТЕЛЬДревняя Греция:XVII в. Готфрид Вильгельм
- 4. ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ: ВЫСКАЗЫВАНИЕ – ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ,
- 5. На марсе была жизнь.Динозавры были теплокровными животными.1
- 6. Высказывание может принимать одно из двух возможных
- 7. ЛОГИЧЕСКИЕ ОПЕРАЦИИ: Конъюнкцией двух высказываний А и
- 8. ЛОГИЧЕСКИЕ ОПЕРАЦИИ: Дизъюнкцией двух высказываний А и
- 9. ЛОГИЧЕСКИЕ ОПЕРАЦИИ: Отрицанием, или инверсией высказывания А
- 10. Логическое выражение – форма записи высказывания.Логические выражения
- 11. ПРИОРИТЕТ ОПЕРАЦИЙ: -- находятся значения выражений в
- 12. НАЙДИТЕ ЗНАЧЕНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ: 1. (3x – 2y >5) AND (x-y
- 13. ПРАКТИЧЕСКОЕ ЗАДАНИЕ: В текстовом процессоре MS Word
- 14. ЗАДАНИЕ НА ДОМ: Выучить основные понятия
- 15. Утверждение, заключенное в красную рамку
- 16. ЛОГИЧЕСКИЕ ОПЕРАЦИИ: Импликация -- связывает два простых
- 17. ЛОГИЧЕСКИЕ ОПЕРАЦИИ: Эквивалентность -- операция сравнения двух
- 18. Литература: Н.Макарова. Информатика 7-9. «Питер», 2004 г
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ОСНОВЫ
ЛОГИКИ
Разработка: Клинковская М.В. – учитель информатики и ИКТ
МОУ гимназии № 7 г. Балтийска
уч.годСлайд 2ЛОГИКА -- ЭТО УЧЕНИЕ О СПОСОБАХ РАССУЖДЕНИЙ И ДОКАЗАТЕЛЬСТВ,
НАУКА О ЗАКОНАХ И ФОРМАХ МЫШЛЕНИЯ
«LOGOS»
-- СЛОВО, МЫСЛЬ, ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОНСлайд 3РАЗВИТИЕ ЛОГИКИ:
СОКРАТ
ПЛАТОН
АРИСТОТЕЛЬ
Древняя Греция:
XVII в. Готфрид Вильгельм Лейбниц:
«Рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам»
XIX в. – логика формируется как самостоятельный раздел математики. Джордж Буль: «Математический анализ логики» - 1847г., «Исследование законов мышления, базирующихся на математической логике и теории вероятности» - 1854г.
Слайд 4ОСНОВНЫЕ ПОНЯТИЯ ЛОГИКИ:
ВЫСКАЗЫВАНИЕ – ПОВЕСТВОВАТЕЛЬНОЕ ПРЕДЛОЖЕНИЕ, В КОТОРОМ ЧТО-ЛИБО
УТВЕРЖДАЕТСЯ ИЛИ ОТРИЦАЕТСЯ.
Свойство высказывания: ПРО ВЫСКАЗЫВАНИЕ ВСЕГДА МОЖНО СКАЗАТЬ,
ИСТИННО ОНО ИЛИ ЛОЖНОСлайд 5На марсе была жизнь.
Динозавры были теплокровными животными.
1 марта 1 года
новой эры на территории современной Москвы прошел дождь.
В тихом омуте
черти водятсяС помощью философского камня можно превратить свинец в золото.
Слайд 6Высказывание может принимать одно из двух возможных логических значений:
ИСТИНА или ЛОЖЬ
ИСТИНА
ЛОЖЬ
ЛОГИЧЕСКИЕ ПОСТОЯННЫЕ
Или
ЛОГИЧЕСКИЕ КОНСТАНТЫ
Слайд 7ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Конъюнкцией двух высказываний А и В называется новое
высказывание А&В, которое истинно тогда и только тогда, когда истинны
оба исходных (простых) высказывания.Конъюнкция – логическое умножение
«И»
AND
Слайд 8ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
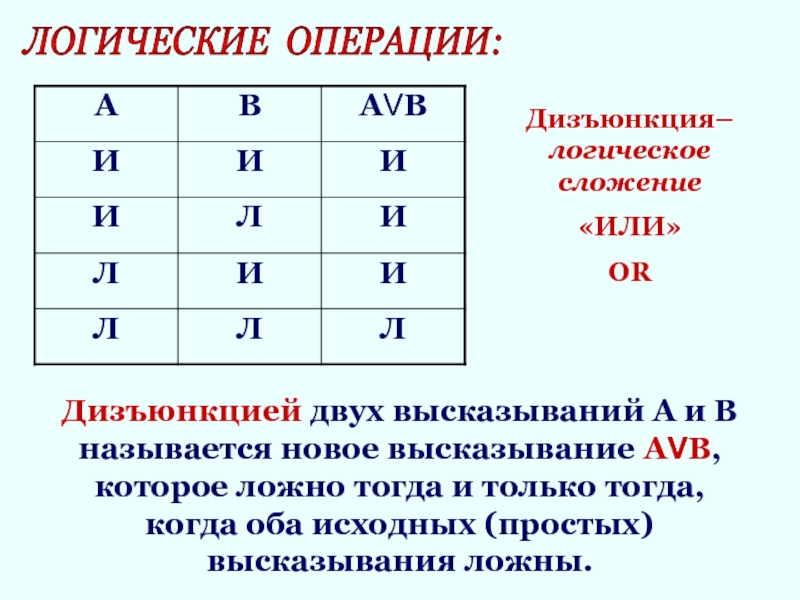
Дизъюнкцией двух высказываний А и В называется новое
высказывание АVВ, которое ложно тогда и только тогда, когда оба
исходных (простых) высказывания ложны.Дизъюнкция– логическое сложение
«ИЛИ»
OR
Слайд 9ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
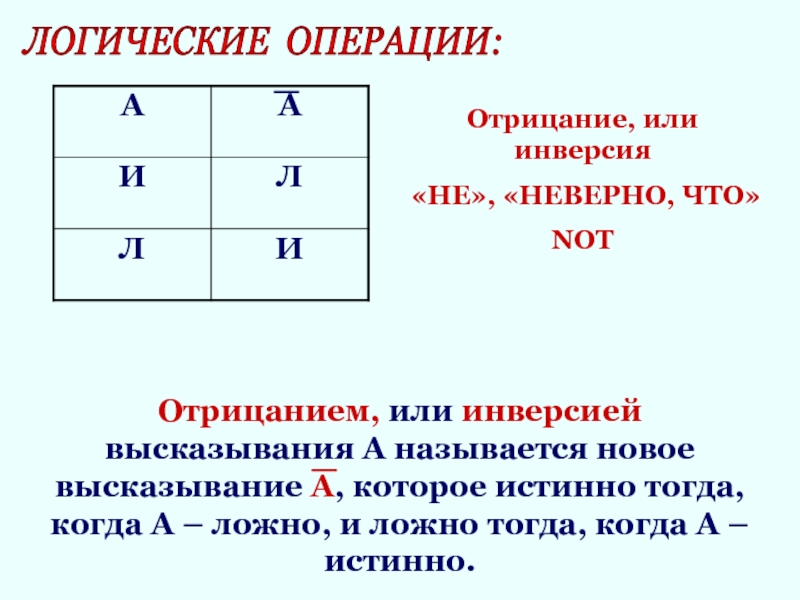
Отрицанием, или инверсией высказывания А называется новое высказывание
А, которое истинно тогда, когда А – ложно, и ложно
тогда, когда А – истинно.Отрицание, или инверсия
«НЕ», «НЕВЕРНО, ЧТО»
NOT
Слайд 10Логическое выражение – форма записи высказывания.
Логические выражения составляются из простых
высказываний с помощью логических операций,
а так же операций отношения (>, <, >=, <=, <>) и круглых скобок.Логическое выражение может иметь значение «Истина» или «ЛОЖЬ» (обозначение 1 и 0 соответственно)
Пример 1. Найдите значение логического выражения: (3x – 2y > 5) AND (x-y <= 0) OR (2x + 5y < 4) при х = 2, у = 3.
Слайд 11ПРИОРИТЕТ ОПЕРАЦИЙ:
-- находятся значения выражений в скобках;
-- выполняются логические
операции:
- отрицание (NOT),
- конъюнкция (AND),- дизъюнкция (OR).
Слайд 12НАЙДИТЕ ЗНАЧЕНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ:
1. (3x – 2y >5) AND
(x-y
при x = 2, y = 3.2. (5a -8b >12) OR (a + b <= 4) AND (2ab < 3) OR (8b – a =4),
при a= 5, b = 4.
3. NOT (12m < 4n) AND (3n +2 > 2m) OR (5n -2m <= 7),
при m = 2, n = 5
Слайд 13ПРАКТИЧЕСКОЕ ЗАДАНИЕ:
В текстовом процессоре MS Word изобразите таблицы (таблицу)
истинности для логических операций:
КОНЪЮНКЦИИ, ДИЗЪЮНКЦИИ, ИНВЕРСИИ.
Полученный файл сохраните на рабочем
столе под своей фамилией.Слайд 14 ЗАДАНИЕ НА ДОМ:
Выучить основные понятия математической логики:
-- определения основных логических операций, таблицы истинности, -- приоритет операций;
-- придумайте 3 логических выражения и найдите значение каждого из них (задание оформить в тетради).
Слайд 15Утверждение, заключенное в красную рамку на этом
слайде, истинно.
Утверждение, заключенное в синюю рамку на
этом слайде, ложно.
Слайд 16ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
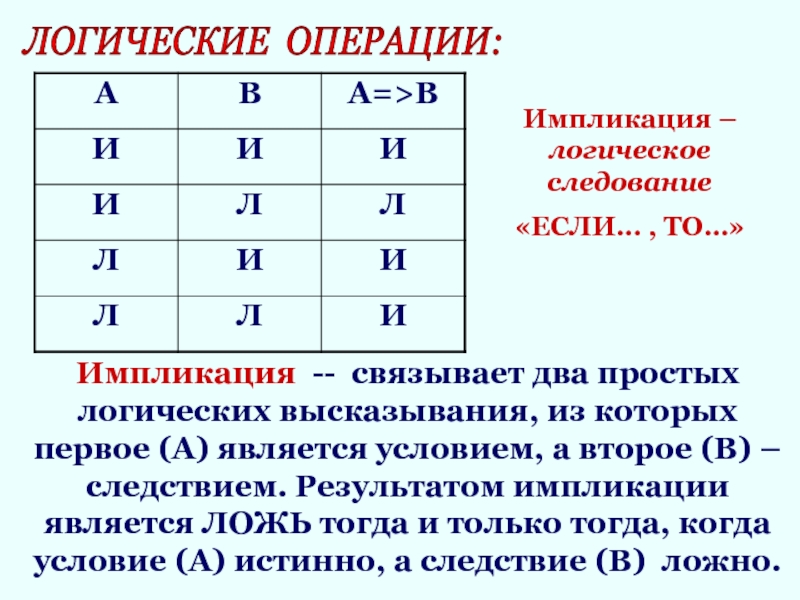
Импликация -- связывает два простых логических высказывания, из
которых первое (А) является условием, а второе (В) – следствием.
Результатом импликации является ЛОЖЬ тогда и только тогда, когда условие (А) истинно, а следствие (В) ложно.Импликация – логическое следование
«ЕСЛИ… , ТО…»
Слайд 17ЛОГИЧЕСКИЕ ОПЕРАЦИИ:
Эквивалентность -- операция сравнения двух логических высказываний А
и В, результатом которой является новое логическое высказывание А⬄В, которое
истинно тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.Эквивалентность – равнозначность
Слайд 18Литература:
Н.Макарова. Информатика 7-9. «Питер», 2004 г .
Информатика. Задачник-практикум в
2 т. / Под ред. И.Г.Семакина, Е.К.Хеннера: Том 1, 2.
– М.: БИНОМ. Лаборатория знаний, 2004.Энциклопедия для детей.[ том 11. ] Математика – 2-е изд., перераб./ ред.коллегия: М.Аксенова, В.Володин, М.Самсонов. – М.: Мир энциклопедий Аванта+, Астрель, 2007 – 621 [3] с.: ил.
Энциклопедия для детей.[ том 22] Информатика / ред. Коллегия: М.Аксенова, Е.Журавлева, А.Леонов. – М.: Мир энциклопедий Аванта+, Астрель, 2008 – 624 с.: ил.