Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики. Методы решение логических задач
Содержание
- 1. Основы логики. Методы решение логических задач
- 2. «Логика – бог мыслящих». Леон Фейхтвангер Цель:познакомиться с методами решения логических задач.
- 3. Краткий исторический экскурс.Слово "логика" греческого происхождения. Логика
- 4. Краткий исторический экскурс.Готфрид Лейбниц в начале 18
- 5. Краткий исторический экскурс.Известнейшие работы Джорджа Буля (1815-1864):
- 6. Краткий исторический экскурс.Огастес (Август) де Мо́рган, ввел
- 7. Целесообразно повторить:Составное высказывание, образованное в результате операции
- 8. Закон тождества
- 9. Устные задания. Вася забыл
- 10. Символом F обозначено одно из указанных ниже
- 11. Для какого имени истинно высказывание
- 12. Методы решения логических задач: Метод
- 13. Метод рассуждений.Задача. Вадим,
- 14. Метод рассуждений.Задача.Цепочка из трех бусин, помеченных латинскими
- 15. Метод таблиц.Задача.
- 16. Решение: Пронумеруем условия задачи.Петров – машинист поезда,
- 17. 1000010000000000001000000001000000001000000100000010000001000010000100110000110010010100000010001001
- 18. Задача.Четверо друзей Алексей, Олег, Игорь и Семен
- 19. Метод графов.Задача. Четыре футбольных команды:
- 20. Италия «Милан»Испания «Реал»Россия «Зенит»Англия «Челси»Италия АнтониоИспания РодригоРоссия
- 21. Метод блок – схем.Задача. Имеются
- 22. Результаты выполнения команд по блок – схеме:Ответ:
- 23. Метод кругов Эйлера
- 24. Каждая семья из нашего дома выписывает газету
- 25. С помощью алгебры логики.Задача. Составить
- 26. Задача. Следователь допрашивает Клода, Жака и Дика.
- 27. ИтогиИдея метода рассуждений состоит в том, что
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Методы Решения логических задач
Георгиевский район
с. Краснокумское
2018 г.
Учитель высшей категории
МБОУ
СОШ №26 с. Краснокумского
Слайд 2«Логика – бог мыслящих».
Леон Фейхтвангер
Цель:
познакомиться с методами решения логических
задач.
Слайд 3Краткий исторический экскурс.
Слово "логика" греческого происхождения. Логика как наука основана
Аристотелем (384-320 гг до н.э.), который был необыкновенной фигурой в
целой плеяде блестящих греческих ученых. Он был последователем Платона и посещал его Академию в Афинах. После смерти Платона (347 г.до н.э.) Аристотель покинул Афины. Он вернулся туда 12 лет спустя и основал свою школу - Лицей. Одним из учеников Аристотеля был Александр Великий.Логика Аристотеля является скорее частью философии, но эта часть - основа всех наук. В своем выдающемся произведении "Аналитики" Аристотель создал и проверил около 20 схем рассуждений, которые назвал силлогизмами. Процитируем самый известный силлогизм: "Сократ - человек; все люди смертны; значит Сократ смертен". После Аристотеля силлогизмы и их трансформации стали основой дедуктивных рассуждений.
Слайд 4Краткий исторический экскурс.
Готфрид Лейбниц в начале 18 века сделал попытку
создать формальную логическую систему, введя законы сочетания высказываний. Он высказал
идею о том, что рассуждения могут быть сведены к механическому выполнению определенных действий по установленным правилам: "Можно придумать некий алфавит человеческих мыслей, и с помощью комбинации букв этого алфавита и анализа слов, из них составленных, все может быть открыто и разрешимо". Но эти работы не были опубликованы, и лишь в 19 веке Джордж Буль и Август де Морган основали математическую логику, независимую от философии.Слайд 5Краткий исторический экскурс.
Известнейшие работы Джорджа Буля (1815-1864): "Формальная логика", "Исследование
законов мысли". Буль вводит в логику алгебраическую структуру, называемую сегодня
кольцо Буля, две операции, свойства которых в чем-то подобны свойствам операции с числами (например, 1+0=1), и в чем-то расходятся с ними (например, 1+1=1). Это позволило описать логику высказываний как формальную алгебраическую структуру.Слайд 6Краткий исторический экскурс.
Огастес (Август) де Мо́рган, ввел кванторы (не называя
их) и сделал попытку формального определения структур, продолжив работу, начатую
Булем.Слайд 7Целесообразно повторить:
Составное высказывание, образованное в результате операции логического умножения (КОНЪЮНКЦИИ),
истинно тогда и только тогда, когда истинны все входящие в
него простые высказывания.Составное высказывание, образованное в результате логического сложения (ДИЗЪЮНКЦИИ), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.
Логическое отрицание (ИНВЕРСИЯ) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Составное высказывание, образованное с помощью операции логического следования (ИМПЛИКАЦИИ), ложно тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание)
Составное высказывание, образованное с помощью логической операции тождества(ЭКВИВАЛЕНТНОСТИ) истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны
Слайд 8Закон тождества
A=A
Закон непротиворечия A&¬A=0
Закон исключенного
третьего Av¬A=1 Закон двойного отрицания ¬¬A=A
Законы де Моргана ¬(¬Av¬B)=¬A&¬B; ¬(¬A&¬B)=¬Av¬B
Закон коммутативности
Закон ассоциативности
Закон
дистрибутивности
Целесообразно повторить:
Слайд 9Устные задания.
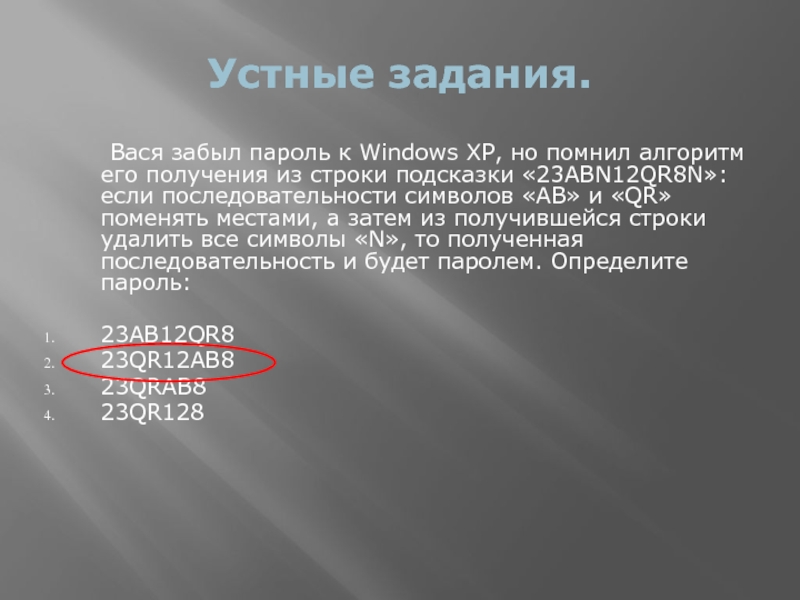
Вася забыл пароль к Windows
XP, но помнил алгоритм его получения из строки подсказки «23ABN12QR8N»:
если последовательности символов «AB» и «QR» поменять местами, а затем из получившейся строки удалить все символы «N», то полученная последовательность и будет паролем. Определите пароль:23AB12QR8
23QR12AB8
23QRAB8
23QR128
Слайд 10Символом F обозначено одно из указанных ниже логических выражений от
трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения
F:Какое выражение соответствует F?
1)¬X ¬Y ¬Z
2) X Y Z
3) X Y Z
4) ¬X ¬Y ¬Z
Слайд 11Для какого имени истинно высказывание
¬(ПЕРВАЯ БУКВА
СОГЛАСНАЯ ВТОРАЯ БУКВА СОГЛАСНАЯ) ПОСЛЕДНЯЯ БУКВА ГЛАСНАЯ?
Запишем в
виде логических операций: ¬ (сс ) гл
1). Роман
2). Юнона
3). Андрей
4). Кристина
Слайд 12Методы решения
логических задач:
Метод рассуждений;
Метод таблиц;
Метод графов;
Метод блок-схем;
Метод кругов Эйлера - Венна;
С помощью алгебры
логики;Итоги
Слайд 13Метод рассуждений.
Задача.
Вадим, Сергей и Михаил
изучают различные иностранные языки: китайский, японский и арабский. На вопрос,
какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский. Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложно. Какой язык изучает каждый из молодых людей.Решение.
А = « Вадим изучает китайский»;
В = «Сергей не изучает китайский»;
С = «Михаил не изучает арабский».
Если верно А, то верно и В. То есть А ложно.
Если верно В, то А и С ложные утверждения (неверно, т.к. никто не изучает китайский).
Таким образом, вено С, а А и В ложные утверждения.
Ответ: Сергей изучает китайский, Михаил – японский, а Вадим – арабский языки.
Слайд 14Метод рассуждений.
Задача.
Цепочка из трех бусин, помеченных латинскими буквами, формируется по
следующему правилу. В конце цепочки стоит одна из бусин A,
B, C. На первом месте – одна из бусин B, D, C, которой нет на третьем месте. В середине – одна из бусин А, C, E, B, не стоящая на первом месте. Какая из перечисленных цепочек создана по этому правилу?1) BCB 2) EAC 3) BCD 4) CBB
Решение.
У1: третья бусина – A, B или C 1) BCB не выполняется У3
У2: первая бусина – B, D или C 2) EAC не выполняется У2
У3: первая и третья бусины – разные 3) BCD не выполняется У1
У4: вторая бусина – A, B, C или E 4) CBB все условия выполняются
У5: первая и вторая бусины – разные
Ответ: 4
Слайд 15Метод таблиц.
Задача.
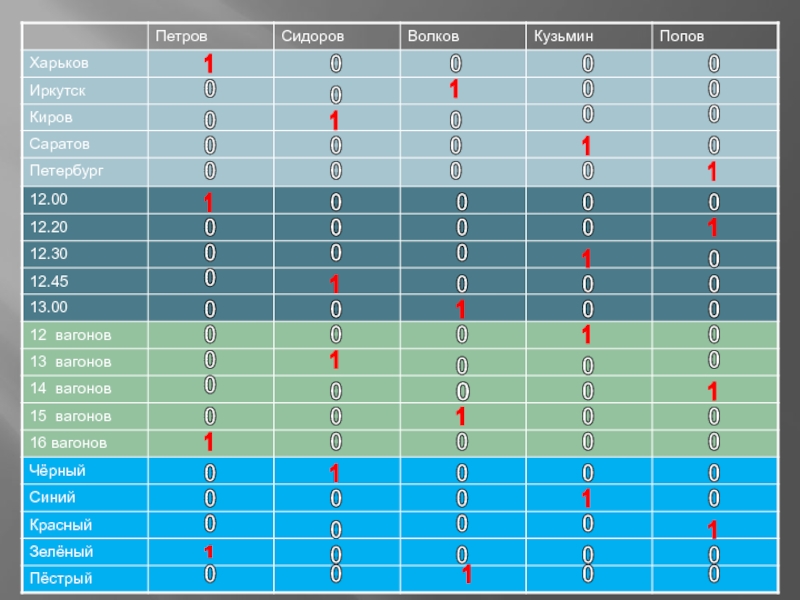
На пяти железнодорожных путях стоят 5 поездов. Петров
– машинист поезда, отправляющегося в 12.00, этот поезд зеленого цвета. В составе поезда, стоящего по центру, 12 вагонов. Сидоров - машинист поезда, отправляющегося в 12.45. Волков – машинист в поезде с 15 вагонами, его поезд сразу слева от поезда зеленого цвета. Сразу правее поезда, имеющего синий цвет, стоит поезд, отправляющийся в Киров. Кузьмин – машинист поезда, едущего в Саратов. Рядом с составом черного цвета – состав с 14 вагонами. Поезд на Иркутск отходит в 13.00. В 12.20 отправляется поезд с машинистом Поповым и он непосредственно справа от поезда до Кирова. Состав с 16 вагонами направляется в Харьков. Рядом с поездом, который отправляется в 12.20, поездной состав с 13 вагонами. Крайний состав окрашен в красный цвет. Состав с 12 вагонами отправляется в 12.30. Составы красного и черного цвета стоят рядом. Поезд, следующий до Харькова, отходит в12.00. Какой состав пестрый? Какой поезд едет в Петербург?Слайд 16Решение:
Пронумеруем условия задачи.
Петров – машинист поезда, отправляющегося в 12.00, этот
поезд зеленого цвета.
В составе поезда, стоящего по центру, 12
вагонов. Сидоров – машинист поезда, отправляющегося в 12.45.
Волков – машинист в поезде с 15 вагонами, его поезд сразу слева от поезда зеленого цвета.
Сразу правее поезда, имеющего синий цвет, стоит поезд, отправляющийся в Киров.
Кузьмин – машинист поезда, едущего в Саратов.
Рядом с составом черного цвета – состав с 14 вагонами.
Поезд на Иркутск отходит в 13.00.
В 12.20 отправляется поезд с машинистом Поповым и он непосредственно справа от поезда до Кирова.
Состав с 16 вагонами направляется в Харьков.
Рядом с поездом, который отправляется в 12.20, поездной состав с 13 вагонами.
Крайний состав окрашен в красный цвет.
Состав с 12 вагонами отправляется в 12.30.
Составы красного и черного цвета стоят рядом.
Поезд, следующий до Харькова, отходит в12.00.
Слайд 171
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
1
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
1
0
0
1
Слайд 18Задача.
Четверо друзей Алексей, Олег, Игорь и Семен занимались в разных
спортивных секциях. Один из них играл в баскетбол, второй —
в волейбол, третий — в футбол, а четвертый — в теннис. У них были и различные увлечения: один из них любил кино, другой — театр, третий — эстраду, а четвертый — цирк. Известно, что Алексей не играет ни в волейбол, ни в баскетбол. Олег играет в футбол и любит театр. Семен не играет в волейбол. Тот из ребят, который играет в волейбол, любит ходить в кино, а тот, кто играет в баскетбол, не любит цирк. В какую секцию ходит и чем увлекается каждый из друзей?Решение.
Алексей не играет ни в волейбол, ни в баскетбол.
Олег играет в футбол и любит театр.
Семен не играет в волейбол.
Тот из ребят, который играет в волейбол, любит ходить в кино.
Тот, кто играет в баскетбол, не любит цирк.
Ответ: Алексей занимается теннисом и любит ходить в цирк, Олег увлекается
театром и занимается футболом, Игорь – волейбол и кино, Семён – баскетбол и эстрада.
Метод таблиц.
Слайд 19Метод графов.
Задача.
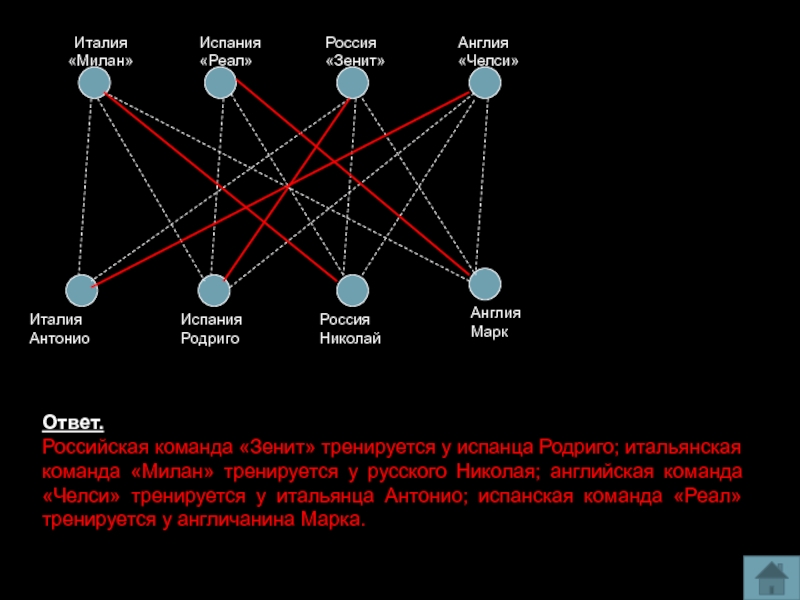
Четыре футбольных команды: итальянская команда «Милан»,
испанская – «Реал», российская – «Зенит», английская – «Челси» встретились
в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно: а) Зенит не тренируется у Марка и Антонио. б) Милан обещал никогда не брать Марка главным тренером.Слайд 20Италия «Милан»
Испания «Реал»
Россия «Зенит»
Англия «Челси»
Италия Антонио
Испания Родриго
Россия Николай
Англия Марк
Ответ.
Российская
команда «Зенит» тренируется у испанца Родриго; итальянская команда «Милан» тренируется
у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда «Реал» тренируется у англичанина Марка.Слайд 21Метод блок – схем.
Задача.
Имеются два сосуда —
трехлитровый и пятилитровый. Нужно, пользуясь этими сосудами, получить 1, 2,
3, 4, 5, 6, 7 и 8 литров воды. В нашем распоряжении водопроводный кран и раковина, куда можно выливать воду.Решение.
НБ — наполнить больший сосуд водой из-под крана;
НМ — наполнить меньший сосуд водой из-под крана;
ОБ — опорожнить больший сосуд, вылив воду в раковину;
ОМ — опорожнить меньший сосуд, вылив воду в раковину;
Б→М — перелить из большего в меньший, пока больший сосуд не опустеет или меньший сосуд не наполнится;
М→Б — перелить из меньшего в больший, пока меньший сосуд не опустеет или больший сосуд не наполнится.
Выделим три команды: НБ, Б→М, ОМ.
Две вспомогательные команды: Б = 0 ? — посмотреть, пуст ли больший сосуд;
М = З ? — посмотреть, наполнен ли малый сосуд.
Последовательность выполнения команд:
Б→М выполнять ОМ всякий раз, как меньший сосуд оказывается наполненным
НБ всякий раз, как больший сосуд будет опорожнен
Слайд 22Результаты выполнения команд по блок – схеме:
Ответ: из таблицы видно,
как наполнить определенное количество воды. А для наполнения 8 литров
необходимо наполнить оба сосуда .Слайд 23 Метод кругов Эйлера - Венна.
Все мои
подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них
разводят лилии, а пятеро — фиалки.И только у двоих есть и лилии и фиалки. Угадайте, сколько у меня подруг?
Л - 6
Ф - 5
2
6-2=
4
4
5-2=
3
3
Всего 4+2+3=9
Слайд 24Каждая семья из нашего дома выписывает газету или журнал, или
и то и другое. 75 семей выписывают газеты,
27 семей
– журналы. Лишь 13 семей и журналы, и газеты. Сколько семей в доме?
Г-75
Ж-27
13
75-13=
62
62
27-13=
14
14
62+13+14= 89 семей
Слайд 25С помощью алгебры логики.
Задача.
Составить расписание занятий так,
чтобы математика была первым или вторым уроком, информатика первым или
третьим уроком, а физика – вторым или третьим.В расписании всего три урока. Сколько вариантов расписания с такими условиями можно составить?
Решение.
М1 = «Математика первым уроком»
М2 = «Математика вторым уроком»
И1 = «Информатика первым уроком»
И3 = «Информатика третьим уроком»
Ф2 = «Физика вторым уроком»
Ф3 = «Физика третьим уроком»
Расписание: (М1 М2) (И1 И3) (Ф2 Ф3)
=(М1 М2) (И1 И3) (Ф2 Ф3) = (М1И1 М1И3 М2И1 М2И3) (Ф2 Ф3) =
М1·И1·Ф2 М1·И3·Ф2 М2·И1·Ф2 М2·И3·Ф2 М1·И1·Ф3 М1·И3·Ф3 М2·И1·Ф3 М2·И3·Ф3
Ответ:
1 вариант – Математика, Физика, Информатика
2 вариант – Информатика, Математика, Физика
Слайд 26Задача. Следователь допрашивает Клода, Жака и Дика. Клод утверждает, что Жак
лжет, Жак обвинял во лжи Дика, а Дик призывает не
слушать ни того, ни другого. Кто из допрашиваемых говорил правду?Решение:
К ¬Ж ¬К Ж
Ж ¬Д ¬Ж Д
Д ¬К ¬Ж ¬Д (К Ж)
(К·¬Ж ¬К·Ж) (Ж·¬Д ¬Ж·Д) (Д·¬К·¬Ж ¬Д·(К Ж)) ≡
(К·¬Ж· Ж·¬Д К·¬Ж·¬Ж·Д ¬К·Ж·Ж·¬Д ¬К·Ж·¬Ж·Д) (Д·¬К·¬Ж ¬Д·К ¬Д·Ж)≡
(К·¬Ж·¬Ж·Д ¬К·Ж·Ж·¬Д) (Д·¬К·¬Ж ¬Д·К ¬Д·Ж) ≡
К·¬Ж·¬Ж·Д·Д·¬К·¬Ж К·¬Ж·¬Ж·Д·¬Д·К К·¬Ж·¬Ж·Д·¬Д·Ж
¬К·Ж·Ж·¬Д·Д·¬К·¬Ж ¬К·Ж·Ж·¬Д·¬Д·К ¬К·Ж·Ж·¬Д·¬Д·Ж ≡
≡ ¬К ¬Д Ж
Ответ: правду говорил Жак.
Слайд 27Итоги
Идея метода рассуждений состоит в том, что мы проводим рассуждения,
используя последовательно все условия задачи, и приходим к выводу,
который и будет являться ответом задачи.Идея метода таблиц состоит в том, чтобы оформлять результаты логических рассуждений с помощью таблицы.
Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Основное преимущество – это наглядность.
Идея метода блок – схем состоит в следующем: описать последовательность выполнения операций, определить порядок их выполнения и фиксировать состояния.
Идея метода кругов Эйлера - требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Но иногда с помощью арифметических действий задачу решить гораздо легче.
При решении задач с помощью алгебры логики обычно используется следующая схема решения:
изучается условие задачи;
вводится система обозначений для логических высказываний;
конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
определяются значения истинности этой логической формулы;
из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.