Презентация к уроку информатики: "Метод greedy".

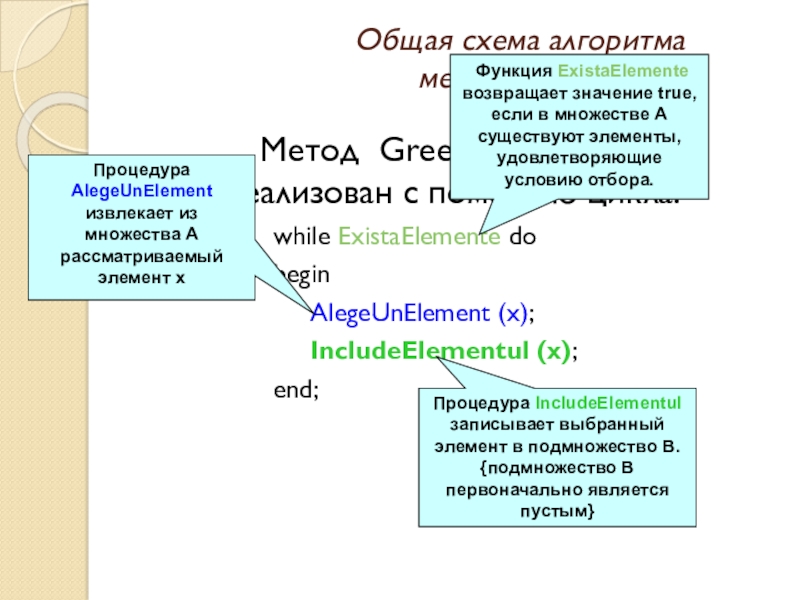
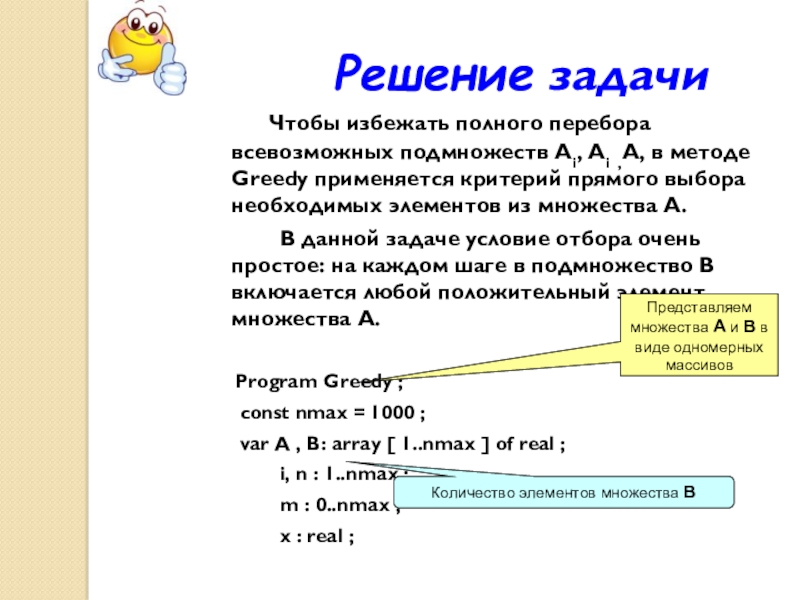
следующую структуру:
задано множество А = { а1, а2,…, ап },

образованное из n элементов;
необходимо определить подмножество В, где В- это подмножество А, удовлетворяющее определённым условиям, которое в результате и будет решением задачи.

может быть реализован с помощью цикла:
while ExistaElemente do
begin

AlegeUnElement (x);
IncludeElementul (x);
end;

Функция ExistaElemente возвращает значение true, если в множестве А существуют элементы, удовлетворяющие условию отбора.

Процедура AlegeUnElement извлекает из множества А рассматриваемый элемент х

Процедура IncludeElementul записывает выбранный элемент в подмножество В. {подмножество В первоначально является пустым}

методе Greedy решение задачи определяется путём последовательной проверки элементов множества

А и включения некоторых из них в подмножество В. Тестируется первый элемент множества А, второй, третий…,пока не будут протестированы все – отсюда и название метода Greedy.

Greedy – жадный, ненасытный

элементы которого являются веществен-ными числами и хотя бы один из

них удовлетворяет условию аi>0. напишите программу, которая вычисляет подмножество В, из множества А, такое, чтобы сумма элементов подмножества В была максимальна.
Например, для А={ 21,5; -3,4; 0; -12,3; 83,6} получим В={ 21,5; 83,6 }

Аi ,А, в методе Greedy применяется критерий прямого выбора необходимых

элементов из множества А.
В данной задаче условие отбора очень простое: на каждом шаге в подмножество В включается любой положительный элемент множества А.

Program Greedy ;
const nmax = 1000 ;
var A , B: array [ 1..nmax ] of real ;
i, n : 1..nmax ;
m : 0..nmax ;
x : real ;

Количество элементов множества В

Представляем множества А и В в виде одномерных массивов

:= false ;
for i:=1 to n do
if A [

i ] > 0 then ExistaElemente := true ;
end ; { ExistaElemente }
procedure AlegeUnElement ( var x : real ) ;
var i : integer ;
begin
i := 1 ;
while A [ i ] <=0 do i := i + 1;
x := A [ i ] ;
A [ i ] := 0 ;
End ; { AlegeUnElement }
procedure IncludeElementul ( x: real ) ;
begin
m := m + 1;
B [ m ] := x ;
End ; { IncludeElementul }

Обратите внимание, процедура AlegeUnElement обнуляет компоненту массива А, содержащую элемент х, извлечённый из соответствующего множества

;
writeln ( ‘Введите элементы множества А:’ );
for i:

= 1 to n do
read ( A[ i ] );
writeln ;
m := 0;
while ExistaElemente do
begin
AlegeUnElement ( x ) ;
IncludeElementul ( x );
end;
writeln ( ‘Элементы множества В :’ );
for i := 1 to n do
writeln ( B[ i ] );
readln;
end.

легко осуществить, иногда требуется предварительная сортировка.
Временная характеристика алгоритмов по методу

Greedy значительно ниже, чем в алгоритмах, использующих при решении тех же задач метод полного перебора.

Удачи при решении задач!