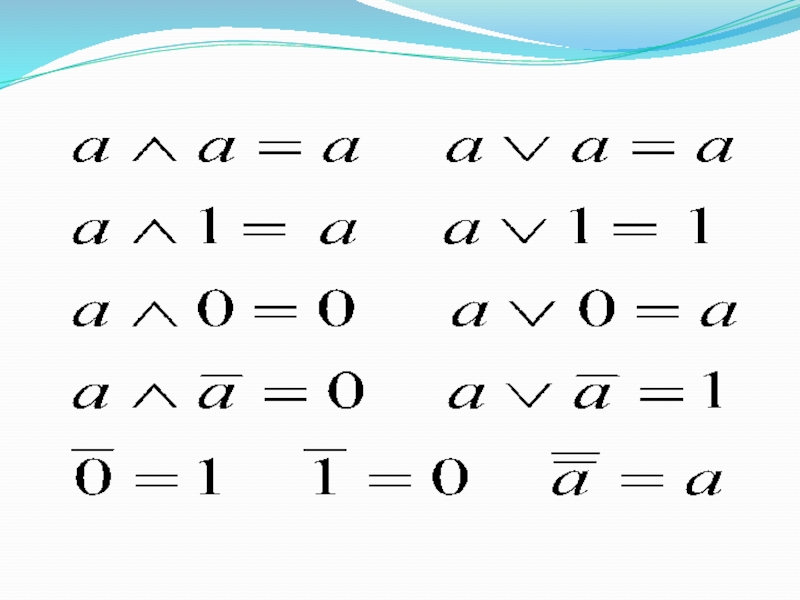Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по разделу "Логика"
Содержание
- 1. Презентация по разделу "Логика"
- 2. Логикаэто наука о формах и способах мышления.
- 3. Зачем она нужна?Изучив логику, можно понять, как
- 4. История развития логикиВ основе современной логики лежат
- 5. История развития логики 1-ый этап развития логики связан
- 6. История развития логики2-ой этапНемецкий учёный Гольфрид
- 7. История развития логики3-ий этап - развил эту
- 8. Слайд 8
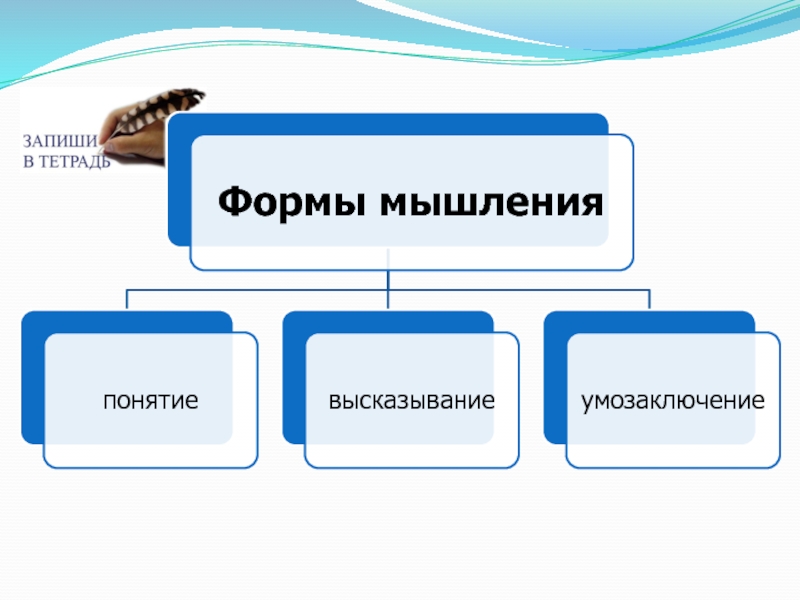
- 9. Понятие- это форма мышления, выделяющая основные, существенные признаки объекта, позволяющие отличать их от остальных.Пример:Квадрат, стол, компьютер.
- 10. ВысказываниеОсновным объектом логики является высказывание. Высказывание – повествовательное
- 11. Высказываниями не являютсяПовелительные, восклицательные или вопросительные предложения:А
- 12. Определите истинность высказыванийБуква А – гласная.Компьютер был
- 13. Какие из предложений являются высказываниями?Какова высота класса?Ответьте
- 14. Содержание высказывания в логике не рассматривается,
- 15. Умозаключение- это форма мышления, с помощью которой
- 16. Правильно ли умозаключение?Если нет, то почему?Барабан –
- 17. Правильно ли умозаключение?Если нет, то почему?Классные комнаты
- 18. Основные операции над высказываниями 1. Логическое отрицание
- 19. 2. Логическая дизъюнкция (сложение)Символьное обозначение:Таблица истинности:Дизъюнкция высказываний
- 20. Пример«4*4=16» или «2*2=3» - истина. (А или В = 1 1
- 21. 3. Логическая конъюнкция (умножение)Символьное обозначениеТаблица истинностиЧитается «и»Конъюнкция
- 22. Составные высказыванияВ алгебре высказываний над высказываниями можно
- 23. Приоритет операций (порядок выполнения)Инверсия (отрицание)Конъюнкция (умножение)Дизъюнкция (сложение). Порядок операций можно изменять с помощью скобок.
- 24. Дополнительные операцииИмпликация (следствие)- если А, то и
- 25. Выберите правильное обозначение«Если вы знаете основы логики,
- 26. Записать в виде логического выражения высказывание«Летом Петя
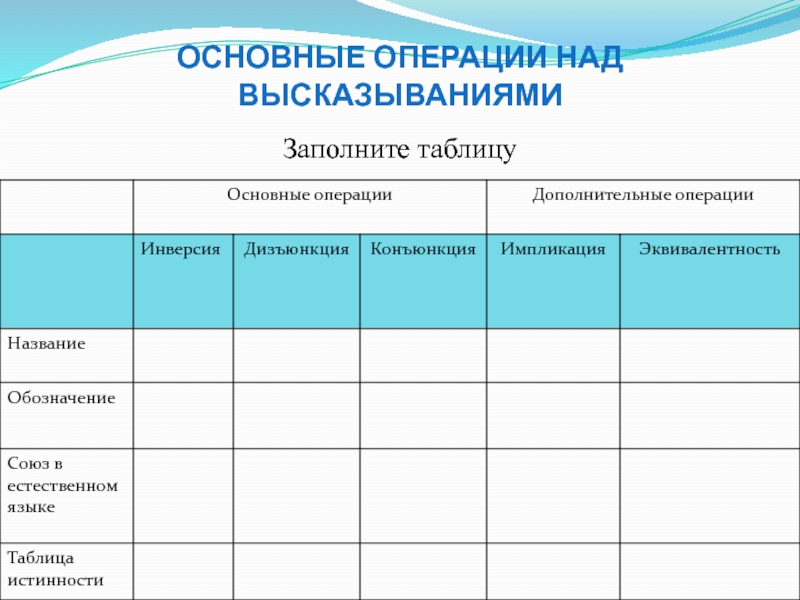
- 27. Основные операции над высказываниямиЗаполните таблицу
- 28. ЗаданиеЕсть 2 высказывания:А – «число 2 –
- 29. Запишите в виде логических выраженийНеверно, что
- 30. Вопросы1. С какой логической операцией можно сравнить
- 31. Законы логикиВыражения называются равносильными, если при одинаковых
- 32. Слайд 32
- 33. 1. Переместительный закон
- 34. 2. Сочетательный закон
- 35. 3. Распределительный закон
- 36. Тождество де Моргана
- 37. Законы поглощения
- 38. ЗадачаЧему равен результат логического умножения А /\
- 39. У братьев Ромы и Саши было 3
- 40. ЗадачаМальчик собирался одеваться, когда погас свет в
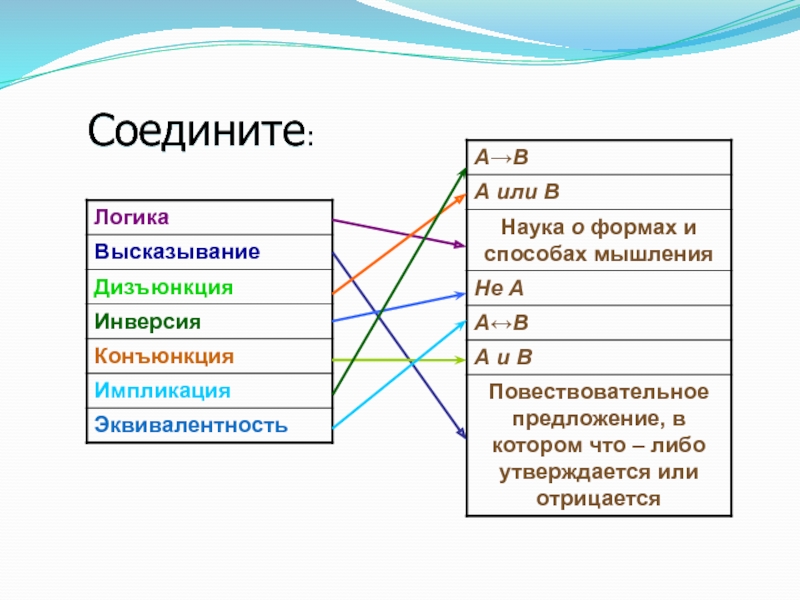
- 41. Соедините:
- 42. Алгоритм построения таблицы истинности логической формулыподсчитать количество
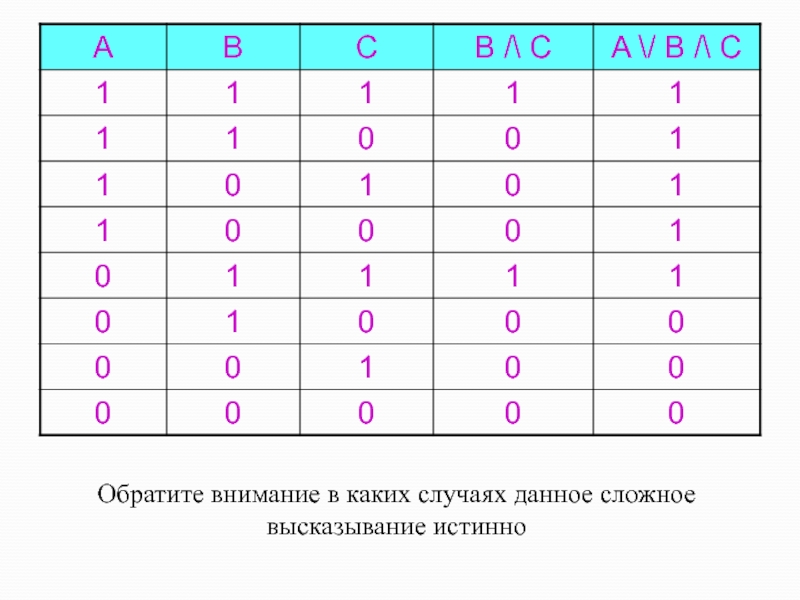
- 43. Обратите внимание в каких случаях данное сложное высказывание истинно
- 44. ЗаданиеУ сестры Юли и Тони было 3
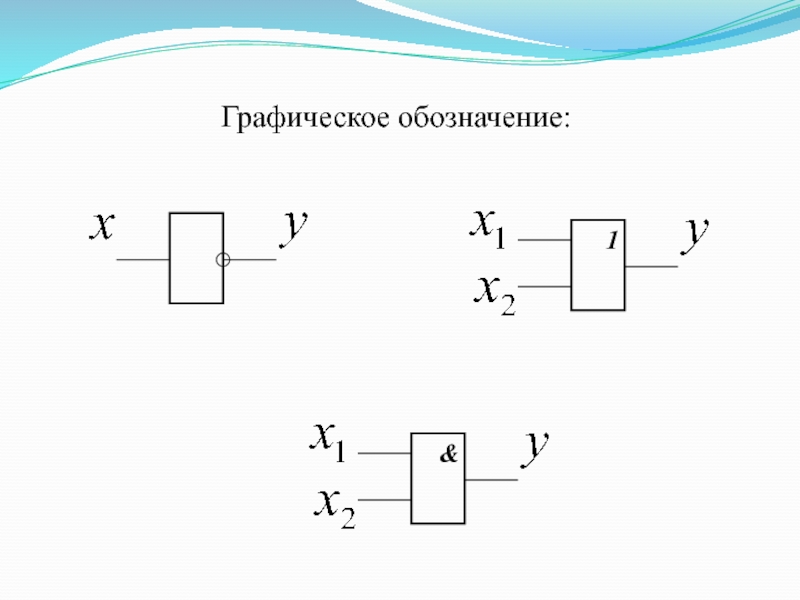
- 45. Графическое обозначение:
- 46. Скачать презентанцию
Логикаэто наука о формах и способах мышления.
Слайды и текст этой презентации
Слайд 3Зачем она нужна?
Изучив логику, можно понять, как устроены электронные схемы
компьютера.
стороны.Слайд 4История развития логики
В основе современной логики лежат учения, созданные ещё
древнегреческими мыслителями, хотя первые учения о формах и способах мышления
возникли в древнем Китае и Индии.Слайд 5История развития логики
1-ый этап развития логики связан с работами учёного
и философа, крупнейшего древнегреческого мыслителя - Аристотеля (384-322 гг. до
н.э.). Он был основоположником формальной логики, изучал правила мышления, «как мы рассуждаем». Дал систематическое изложение логики, анализировал человеческое мышление. Отделил логические формы мышления от его содержания.Слайд 6 История развития логики
2-ой этап
Немецкий учёный Гольфрид Вильгельм Лейбниц в
XVII веке высказал идею о замене рассуждений действиями со знаками
и привёл соответствующие правила.Слайд 7История развития логики
3-ий этап - развил эту идею Джордж Буль
(XIX век). Он изобрёл своеобразную алгебру – систему обозначений и
правил, применяемую ко всевозможным объектам, от чисел и букв до предложений. Его именем она и называется – алгебра Буля или Булева алгебра – начальный раздел математической логики.Выдвинул математическую логику, как науку. В логике появился алфавит и правила записи. Основное назначение этой системы состояло в том, чтобы закодировать логические высказывания, свести логические умозаключения к виду формулы.
Операции, которые он ввёл, пригодились для работы с двоичным кодом. Математическая логика – инструмент при построении микросхем компьютера.
Слайд 9Понятие
- это форма мышления, выделяющая основные, существенные признаки объекта, позволяющие
отличать их от остальных.
Пример:
Квадрат, стол, компьютер.
Слайд 10Высказывание
Основным объектом логики является высказывание.
Высказывание – повествовательное предложение, о котором
можно сказать – истинно оно или ложно.
Например:
На улице идёт
дождь.Скоро каникулы.
Но не всякое предложение является логическим высказыванием.
Включи свет!
Как дела?
Ученик 9 класса.
Информатика – интересный предмет.
не являются высказываниями.
Слайд 11Высказываниями не являются
Повелительные, восклицательные или вопросительные предложения:
А ты записался добровольцем?
Предложения
в которых ничего не утверждается
Ученик 10 класса.
Предложения, в которых используются
неопределённые понятия: У него голубые глаза.
Слайд 12Определите истинность высказываний
Буква А – гласная.
Компьютер был изобретён в середине
XIX века.
2*2=5.
У квадрата одна сторона больше другой в 2 раза.
Солнце
есть спутник земли Сегодня отличная погода
В романе Л.Н. Толстого “Война и мир” 3 432 536 слов
Санкт-Петербург расположен на Неве
Первая космическая скорость равна 7.8 км/сек
Железо — металл
Если один угол в треугольнике прямой, то треугольник будет тупоугольным;
Если сумма квадратов двух сторон треугольника равна квадрату третьей, то он прямоугольный.
Слайд 13Какие из предложений являются высказываниями?
Какова высота класса?
Ответьте на вопрос.
2+3 =
5
Делайте утреннюю зарядку!
Клавиатура – устройство ввода информации.
Чему равно расстояние от
Москвы до Белгорода?Кто отсутствует?
Слайд 14
Содержание высказывания в логике не рассматривается, важно только –
истинно оно или ложно.
Обозначаются высказывания латинскими буквами А, В, С…
Высказывание
принимают за логическую переменную, и если его значение истина, то А=1,
если ложно, то А=0.
Например
высказывание В: 2*2=4 – истина, значит В=1.
высказывание С: 2*4=6 – ложь, значит С=0.
Слайд 15Умозаключение
- это форма мышления, с помощью которой из одного или
нескольких суждений может быть получено новое суждение (заключение, знание, вывод).
Слайд 16Правильно ли умозаключение?
Если нет, то почему?
Барабан – это музыкальный инструмент.
У
Вовы дома музыкальный инструмент.
Значит, у него дома барабан.
Слайд 17Правильно ли умозаключение?
Если нет, то почему?
Классные комнаты надо проветривать.
Квартира –
это не классная комната.
Значит квартиру не надо проветривать.
Слайд 18Основные операции над высказываниями
1. Логическое отрицание (инверсия)
Символьное обозначение
Таблица истинности
Инверсия А
истина тогда и только тогда, когда А – ложно, и
наоборот.Читается: «не Х»
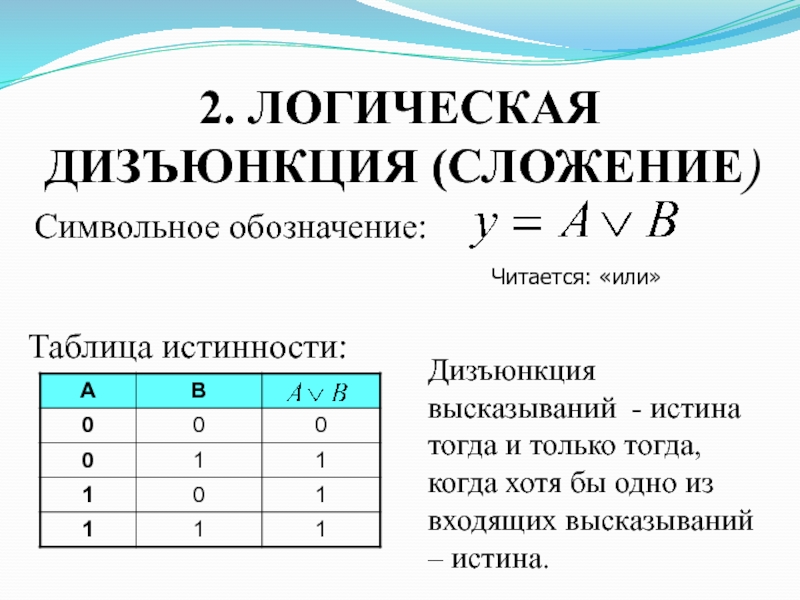
Слайд 192. Логическая дизъюнкция (сложение)
Символьное обозначение:
Таблица истинности:
Дизъюнкция высказываний - истина тогда
и только тогда, когда хотя бы одно из входящих высказываний
– истина.Читается: «или»
Слайд 20Пример
«4*4=16» или «2*2=3» - истина.
(А или В = 1
1 или 0 = 1)
«На улице темно»
или «Сейчас перемена» - ложь.
(0 или 0 = 0)
Слайд 213. Логическая конъюнкция (умножение)
Символьное обозначение
Таблица истинности
Читается «и»
Конъюнкция высказываний истина тогда
и только тогда, когда значения всех входящих высказываний – истина.
Слайд 22Составные высказывания
В алгебре высказываний над высказываниями можно производить определенные логические
операции, в результате которых получаются новые, составные высказывания.
Высказывание, содержащее в
себе другие высказывания, называются составным.Например:
Можно вечером пойти на дискотеку и выучить уроки.
Можно вечером пойти на дискотеку или выучить уроки.
Если можно вечером пойти на дискотеку, то и выучить уроки.
Можно вечером пойти на дискотеку тогда и только тогда, когда выучишь уроки.
Нельзя вечером пойти на дискотеку и выучить уроки.
Обозначим:
А - «можно вечером пойти на дискотеку»
В - «выучить уроки»
Тогда высказывания запишутся:
А и В
А или В
если А, то В
а тогда и только тогда, когда В
не А и В
Слайд 23Приоритет операций
(порядок выполнения)
Инверсия (отрицание)
Конъюнкция (умножение)
Дизъюнкция (сложение).
Порядок операций можно изменять
с помощью скобок.
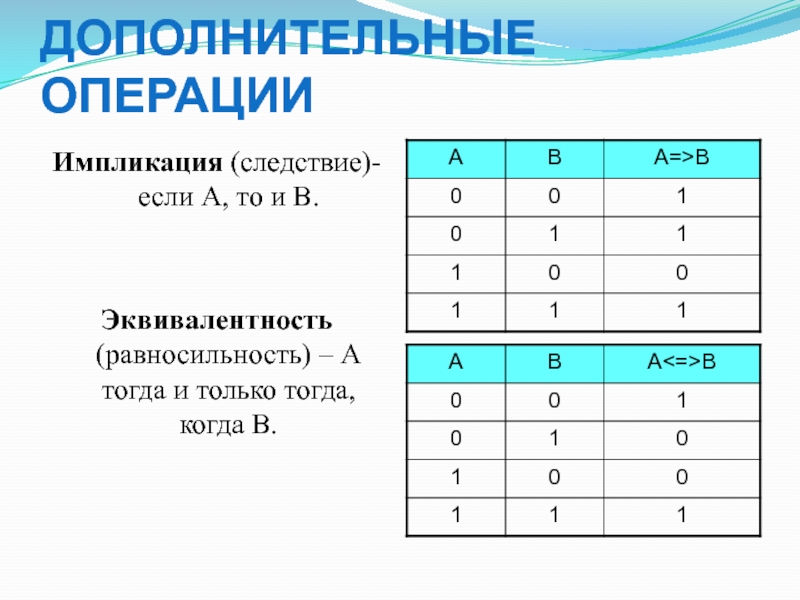
Слайд 24Дополнительные операции
Импликация (следствие)- если А, то и В.
Эквивалентность (равносильность) –
А тогда и только тогда, когда В.
Слайд 25Выберите правильное обозначение
«Если вы знаете основы логики,
то умеете читать логические
схемы
и строить таблицы истинности»?
(A B) \/ (AC)
A B \/ C
(A
B) /\ ACA ( B /\ С).
Слайд 26Записать в виде логического выражения высказывание
«Летом Петя поедет в деревню
и, если будет хорошая погода, то он пойдёт на рыбалку»
Это
высказывание состоит из частей:А - Петя поедет в деревню,
В - будет хорошая погода,
С - он пойдёт на рыбалку.
F = A ^ (B => C).
Слайд 28Задание
Есть 2 высказывания:
А – «число 2 – чётное»,
В – «волк
– травоядное животное».
Составьте все возможные составные высказывания и определите их
истинность.Слайд 29Запишите в виде
логических выражений
Неверно, что корова – хищное животное.
На
уроке физики мы выполняли лабораторную работу и сообщали результаты исследований
преподавателю.При замерзании воды выделяется тепло.
Компьютер выполняет вычисления, если он включён.
Слайд 30Вопросы
1. С какой логической операцией можно сравнить процесс открывания замка,
который открывается двумя ключами одновременно?
2.…любым ключом?
Слайд 31Законы логики
Выражения называются равносильными, если при одинаковых наборах переменных принимают
одинаковые значения.
Логические функции, истинные на всех наборах значений входных переменных,
называются тождественно-истинными.Логические функции, ложные на всех наборах значений входных переменных, называются тождественно-ложными.
Слайд 38Задача
Чему равен результат логического умножения А /\ В /\ С,
если:
А: «N – натуральное»,
В: «N делится на 5»,
С: «N
Слайд 39У братьев Ромы и Саши было 3 машинки:
1 красная и
2 синих.
Увидев у Саши одну из этих машинок Рома понял,
что
он может поиграться только синей машинкой.Какая машинка была у Саши?
Задание
Слайд 40Задача
Мальчик собирался одеваться, когда погас свет в комнате, где в
ящике шкафа лежали его коричневые и синие носки. Какое наименьшее
число носков он должен взять из ящика, чтобы обеспечить себя парой одного цвета?Слайд 42Алгоритм построения таблицы истинности логической формулы
подсчитать количество переменных в формуле.
определить
число строк в таблице 2n, где n – число переменных.
подсчитать
количество логических операций в формуле.установить последовательность выполнения операций с учетом скобок и приоритетов.
определить количество столбцов в таблице: число переменных + число операций.
выписать наборы значений переменных в виде нулей и единиц.
провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с их очередностью.
Слайд 44Задание
У сестры Юли и Тони было 3 платка:
1 красный и
2 синих.
Увидев на Юле один из этих платков Тоня поняла,
что
она может надеть только синий платок.Какой платок был на Юле?