Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Содержание
- 1. Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
- 2. Происхождение1940 г. Родоначальник идеи Джон фон Нейман.
- 3. Правила игры «Жизнь» Место действия- разбитая на
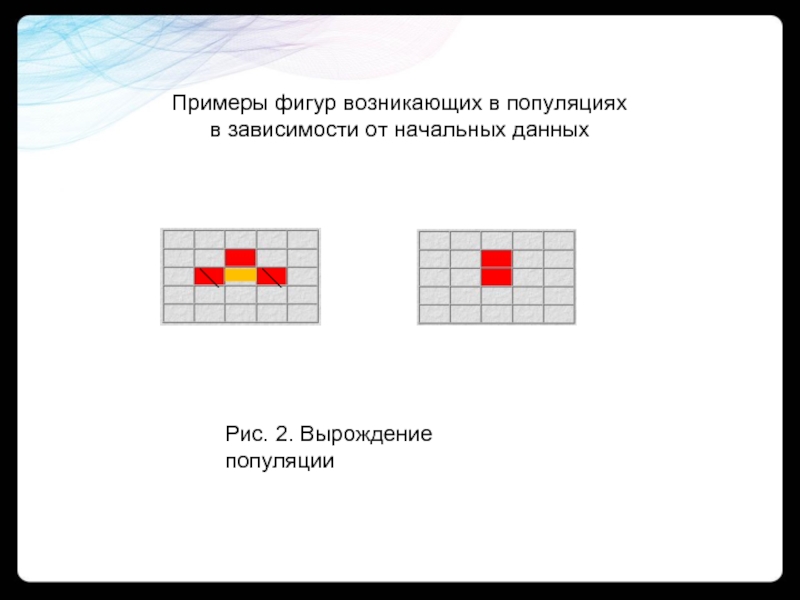
- 4. Рис.1 «Мигалка»Примеры фигур возникающих в популяцияхв зависимости от начальных данных
- 5. Слайд 5
- 6. Слайд 6
- 7. Классификация фигур: устойчивые фигуры; периодические фигуры; двигающиеся фигуры; пожиратели и др.
- 8. Правила игры «Жизнь»Формула №1расчета выживаемости для живой
- 9. Формула №3 проверки мертвая или живая клетка
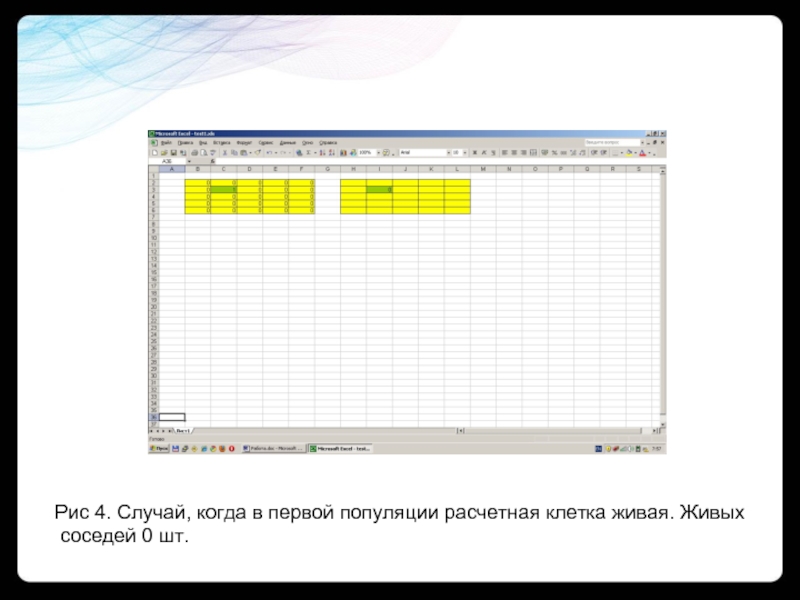
- 10. Рис 4. Случай, когда в первой популяции расчетная клетка живая. Живых соседей 0 шт.
- 11. Науки на которые повлияло развитие игры «Жизнь»
- 12. Выводы и заключенияРассмотренная реализация имеет ряд недостатков:
- 13. Спасибо за внимание!
- 14. Скачать презентанцию
Происхождение1940 г. Родоначальник идеи Джон фон Нейман. Попытка создания гипотетической машины, которая может воспроизводить себя сама. 1970 г. Первая публикация правил игры «Жизнь» в журнале Scientific American Джоном Конвеем. Предложена
Слайды и текст этой презентации
Слайд 1Реализация и изучение игры «Жизнь»
в среде электронных таблиц (MS Ecxel)
Докладчик:
Посевина А.Д.
Номинация: математика
Слайд 2Происхождение
1940 г.
Родоначальник идеи Джон фон Нейман. Попытка создания
гипотетической машины,
которая может воспроизводить себя сама.
1970 г.
Первая публикация правил игры «Жизнь»
в журнале Scientific American Джоном Конвеем. Предложена более простая математическая модель на основе идей Джона фон Неймана.Слайд 3Правила игры «Жизнь»
Место действия- разбитая на ячейки поверхность
Каждая клетка
поверхности может находиться в двух состояниях (мертвая или живая)
Клетка имеет
8 соседейНачальное количество клеток(первое поколение) задаётся
Мёртвая клетка, рядом с которой 3 живые клетки оживает
Если вокруг живой клетки стоят 2,3 живые клетки-соседки, она продолжает жить.
Если вокруг живой клетки стоят больше 3-х живых клеток или меньше 2-х, то клетка умирает.
Популяцией в нашей игре называется квадрат (минимальный размер 3*3 клеток)
Слайд 7
Классификация фигур:
устойчивые фигуры;
периодические фигуры;
двигающиеся фигуры;
пожиратели и др.
Слайд 8Правила игры «Жизнь»
Формула №1расчета выживаемости для живой клетки
расположенной в
ячейке С3: ЕСЛИ(ИЛИ((B1+B3+A1+A2+A3+C1+C2+C3)>3;(CB211+B3+AC2+C3)
1 – живет Формула №2 расчета условия оживания для мертвой клетки расположенной в ячейке С3: ЕСЛИ((B4+B6+A4+A5+A6+C4+C5+C6)=3;1;0) 1 – умирает, 0 – живетСлайд 9Формула №3 проверки мертвая или живая клетка в ячейке B4:
ЕСЛИ(B4=1;"Живая"; "Мертвая")
Подставим формулу №1 и №2 в формулу №3, получим
формулу №4.
Формула №4 вычисления состояния клетки в последующей
популяции в зависимости от того клетка ячейке B4
мертвая или живая и количества живых соседей:
ЕСЛИ(B4=1;ЕСЛИ(ИЛИ((B1+B3+A1+A2+A3+C1+C2+C3)>3;
(CB211+B3+A1+A2+A3+C1+C2+C3)<2);0;1);
ЕСЛИ((B4+B6+A4+A5+A6+C4+C5+C6)=3;1;0))
возвращает 1- живая, 0 - мертвая
Слайд 11Науки на которые повлияло развитие игры
«Жизнь»
Разделы математики и
информатики: теория автоматов, теория алгоритмов, теория игр, алгебра и теория
чисел, теория вероятностей, комбинаторика и теория графов, фрактальная геометрия, вычислительнаяматематика. «Нематематические» дисциплины: кибернетика, химия, биология, астрономия, физика твёрдого тела, квантовая физика, наномеханика, электротехника, социология,
теология, философия.
классификация фигур:
устойчивые фигуры,
периодические фигуры,
двигающиеся фигуры,
пожиратели и др.
Слайд 12Выводы и заключения
Рассмотренная реализация имеет ряд недостатков: невозможный расчёт большого
количества популяций, ограниченная численность популяций (в нашем случае 25 элементов),
трудоёмкость и ненадежность реализации.Практическая ценность: данная работа может быть
использована в качестве лабораторного практикума на уроках
математики или информатики по соответствующей теме.
Теги