Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы счисления. Урок информатики 5-11 класс
Содержание
- 1. Системы счисления. Урок информатики 5-11 класс
- 2. Что такое системы счисления?Запись числа в развернутой формеПозиционные системы счисленияНепозиционные системы счисления
- 3. Система счисления – это способ записи чисел
- 4. Единичная система счисленияНЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ 10 –
- 5. Древнеегипетская система счисления -1205НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ -23029
- 6. Древнегреческие системы счисленияНЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Древнегреческая аттическая
- 7. Славянская система счисленияНЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
- 8. НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Римская система счисления Юбилейная
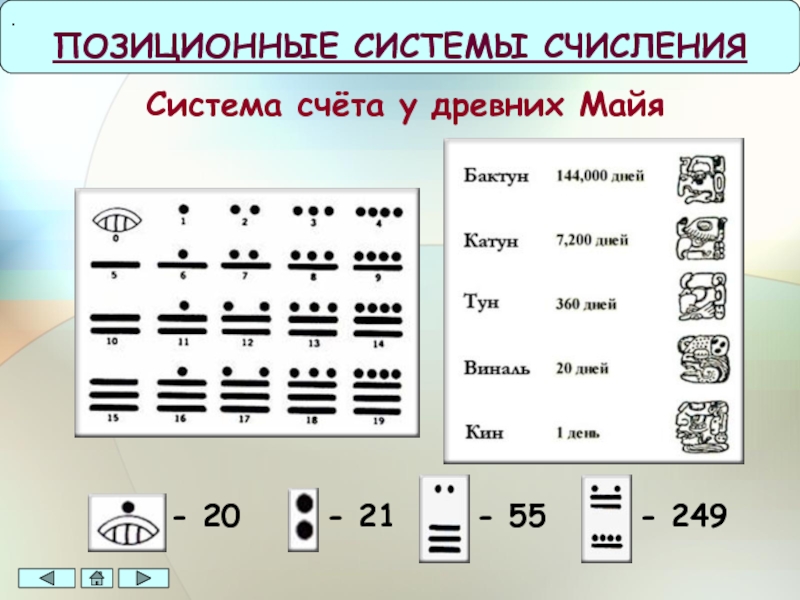
- 9. Система счёта у древних Майя- 20ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ . - 21- 55- 249
- 10. - - единицыПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ - десятки- нольВавилонская система счисления- 3- 20- 32- 7203- 3725
- 11. Древнекитайская система счисленияПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Великая Китайская стена – символ Китая-1000-548
- 12. Десятичная система счисленияПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
- 13. Основание системы – это количество различных знаков,
- 14. Любое десятичное число можно представить в виде
- 15. Запись числа в развернутой форме
- 16. Любое двоичное число можно представить в виде
- 17. В q-ичной системе счисления числа в развернутой
- 18. Запись числа в развернутой форме
- 19. Запись числа в развернутой форме
- 20. 1. Какое минимальное основание может иметь система
- 21. Скачать презентанцию
Что такое системы счисления?Запись числа в развернутой формеПозиционные системы счисленияНепозиционные системы счисления
Слайды и текст этой презентации
Слайд 2
Что такое системы счисления?
Запись числа в развернутой форме
Позиционные системы счисления
Непозиционные
системы счисления
Слайд 3
Система счисления – это способ записи чисел по определенным правилам
с помощью заданного набора специальных знаков (цифр)
вес цифры не
зависит отеё позиции в числе
вес каждой цифры изменяется
в зависимости от её положения
Системы счисления
непозиционныенепозиционные позиционные
Единичная
Древнеегипетская
Древнегреческая
Славянская
Римская
Двадцатеричная народов племени Майя
Вавилонская
Древнекитайская
десятеричная
Десятичная
Двоичная
и др.
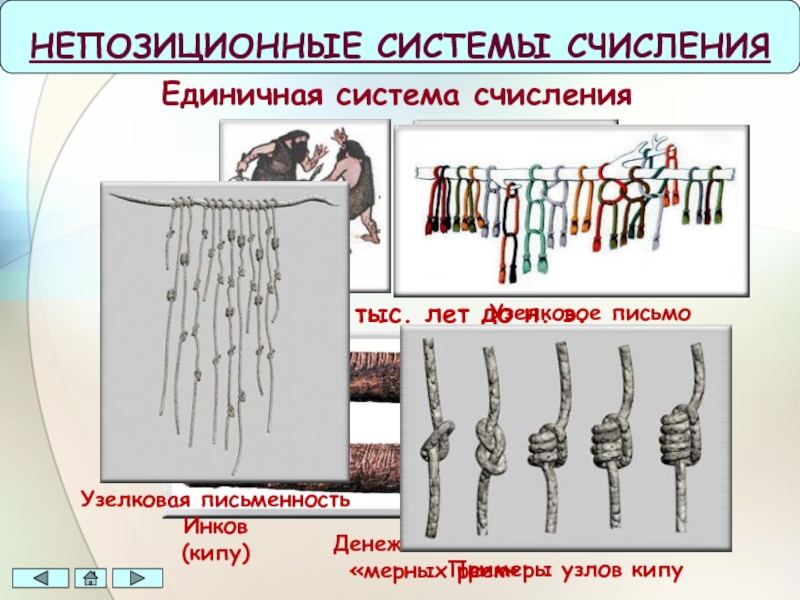
Слайд 4Единичная система счисления
НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
10 – 11 тыс. лет до
н. э.
Узелковое письмо
Денежная система
«мерных реек»
Узелковая письменность Инков
(кипу)
Примеры узлов кипу
Слайд 6Древнегреческие системы счисления
НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Древнегреческая аттическая пятеричная
- 256
- 2051
-
382
Древнегреческая ионийская десятеричная алфавитная
- 265
- 503
- 731
Слайд 8
НЕПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Римская система счисления
Юбилейная медаль
«Тридцать лет победы в Великой
Отечественной войне 1941 – 1945 гг.»
Куранты на Спасской башне Московского
КремляПамятник Петру I
«Медный всадник»
в Санкт-Петербурге
Евангелическо-лютеранский Храм в честь Святой троицы
Город Москва
Слайд 10- - единицы
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
- десятки
- ноль
Вавилонская система счисления
- 3
-
20
- 32
- 7203
- 3725
Слайд 11Древнекитайская система счисления
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Великая Китайская стена –
символ Китая
-1000
-548
Слайд 13Основание системы – это количество
различных знаков, используемых для
изображения
чисел в данной системе.
ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ
Двоичная 0, 1
Восьмеричная
0, 1, 2, 3, 4, 5, 6, 7
Шестнадцатеричная
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Десятичная
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Слайд 14Любое десятичное число можно представить в виде суммы степеней числа
10 – основания системы.
Запись числа в развернутой форме
Десятичная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Свернутая форма
77710
Развернутая форма
77710=
7∙102+7∙101+7∙100
Слайд 15
Запись числа в развернутой форме
Десятичная
0,
1, 2, 3, 4, 5, 6, 7, 8, 9Свернутая форма
777,7710
Развернутая форма
=7∙102+7∙101+7∙100+7∙10-1+7∙10-2
A10=an-1an-2…a0,a-1…a-m
777,7710=
A10=an-1∙10n-1+an-2∙10n-2+…+a0∙100 +a-1∙10-1+…+a-m∙10-m
Слайд 16Любое двоичное число можно представить в виде суммы степеней числа
2 – основания системы.
Запись числа в развернутой форме
Свернутая форма
101,12
Развернутая
форма101,12=
1∙22+0∙21+1∙20 +1∙2-1
Двоичная
0, 1
A2=an-1an-2…a0,a-1…a-m
A2=an-1∙2n-1+an-2∙2n-2+…+a0∙20 +
a-1∙2-1+…+a-m∙2-m
Слайд 17В q-ичной системе счисления числа в развернутой форме записываются в
виде суммы степеней основания q с коэффициентами, в качестве которых
выступают цифры данного числа.
Запись числа в развернутой форме
Системы счисления с произвольным основанием (q-ичная система счисления)
0, 1, 2, . . . ,q-1
Aq=an-1∙qn-1+an-2∙qn-2+…+a0∙q0 +
a-1∙q-1+…+a-m∙q-m
Слайд 18
Запись числа в развернутой форме
Восьмеричная
0,
1, 2, 3, 4, 5, 6, 7Свернутая форма
374,28
Развернутая форма
374,28=
3∙82+7∙81+4∙80+2∙8-1
Слайд 19
Запись числа в развернутой форме
Шестнадцатеричная
0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Свернутая форма
8A,F16
Развернутая форма
8A,F=
8∙161+A∙160+F∙16-1
8A,F=
8∙161+10∙160+15∙16-1
Слайд 201. Какое минимальное основание может иметь система счисления, если в
ней записаны числа 174; 23; 10012; 97.
2. Запишите числа
в развернутой форме:23,4510
10010,012
54,78
5C,2А16
3.Запишите числа в римской системе счисления:
79310
164210
