Слайд 1Содержательный подход к определению количества информации
Слайд 2 Количество информации, заключенное в сообщении, определяется объемом знаний,
который несет это сообщение человеку. Этот подход субъективный (зависит от
конкретного человека).
Разные люди, получившие одно и то же сообщение, по-разному оценивают количество информации, содержащееся в нем. Это происходит от того, что знания людей о событиях, о которых идет речь в сообщении, различны.
Пример
Второклассник изучает таблицу умножения.
Учитель сообщает ему, что 2 х 2 = 4.
Второклассник этого раньше не знал, поэтому
такое сообщение содержит для него
информацию.
А для ученика 5 класса таблица умножения
хорошо известна, поэтому из такого сообщения
информацию он не получит.
Слайд 3 Сообщение несет информацию для человека, если содержащиеся в нем
сведения являются для него новыми и понятными.
Информация
— это знания человека.
Сообщение информативно (содержит ненулевую информацию), если оно пополняет знания человека.
Слайд 4
Но для того чтобы сообщение было информативно оно должно еще
быть понятно.
Например, прогноз погоды на завтра — информативное сообщение,
а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Слайд 5
Быть понятным, значит быть логически связанным с предыдущими знаниями человека.
Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции
на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Слайд 6С содержательной точки зрения количество информации, заключенное в сообщении, связано
с тем, насколько это сообщение уменьшает неопределенность знания принимающего его
человека.
Слайд 7Неопределенность знаний о некотором событии — это количество возможных результатов
события. (бросания монеты, кубика; вытаскивания жребия)
Слайд 8Неопределенность знания
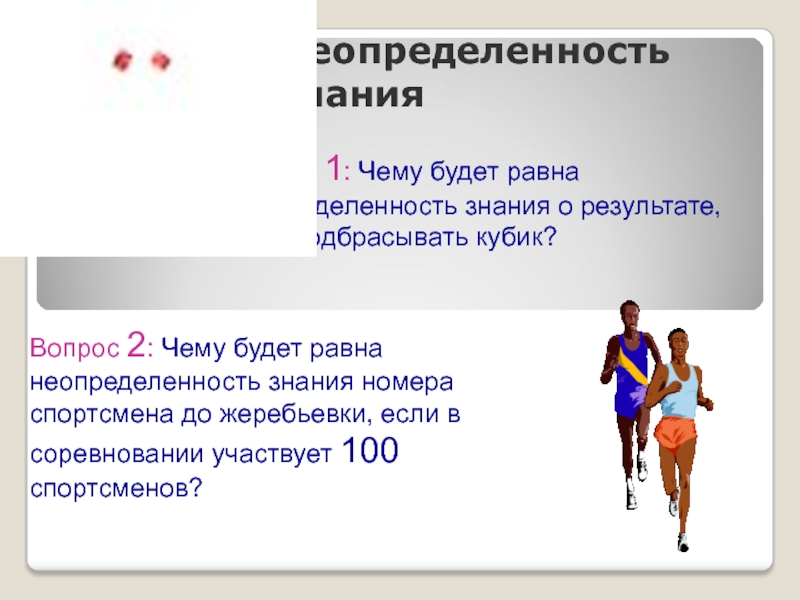
Вопрос 1: Чему будет равна неопределенность знания о результате,
если подбрасывать кубик?
Вопрос 2: Чему будет равна неопределенность знания номера
спортсмена до жеребьевки, если в соревновании участвует 100 спортсменов?
Слайд 9УМЕНЬШЕНИЕ НЕОПРЕДЕЛЁННОСТИ ЗНАНИЯ
События равновероятны, если при возрастающем числе опытов количества
выпадений «орла» и «решки» постепенно сближаются.
Пусть у нас имеется монета,
которую мы бросаем на ровную поверхность.
С равной вероятностью произойдет одно из двух возможных событий – монета окажется в одном из двух положений: «орёл» или «решка».
Перед броском существует неопределённость нашего знания (возможны два события), а после броска наступает полная определённость.
Неопределённость нашего знания уменьшается в два раза, так как из двух возможных равновероятностных событий реализовалось одно.
Слайд 10УМЕНЬШЕНИЕ НЕОПРЕДЕЛЁННОСТИ ЗНАНИЯ
При бросании равносторонней четырехгранной пирамиды существуют 4 равновероятных
события.
При бросании шестигранного игрального кубика существует
6 равновероятных событий.
Слайд 11ЕДИНИЦЫ ИЗМЕРЕНИЯ КОЛИЧЕСТВА ИНФОРМАЦИИ
Сообщение, уменьшающее неопределённость знания в два раза,
несёт 1 бит информации.
Бит – минимальная единица измерения информации.
1 Кбайт
= 210 байт = 1024 байт
1 Мбайт = 210 Кбайт = 1024 Кбайт
1 Гбайт = 210 Мбайт = 1024 Мбайт
1 Тбайт = 1024 Гбайт = 240 байт
1 Пбайт (Петабайт) = 1024 Тбайт = 250 байт.
1 байт = 23 битов = 8 битов
Слайд 12Очевидно, различать лишь две ситуации: «нет информации» — «есть информация»
для измерения информации недостаточно.
Единица измерения информации была определена в
науке, которая называется теорией информации. Эта единица носит название «бит». Ее определение звучит так:
Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации.
Слайд 13После сдачи зачета или выполнения контрольной работы ученик мучается неопределенностью,
он не знает, какую оценку получил.
«Зачет», «незачет»?
«2», «3», «4» или «5»?
Наконец, учитель объявляет результаты, и он получаете одно из двух информационных сообщений: «зачет» или «незачет», а после контрольной работы одно из четырех информационных сообщений: «2», «3», «4» или «5».
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности знания в два раза, так как получено одно из двух возможных информационных сообщений.
Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.
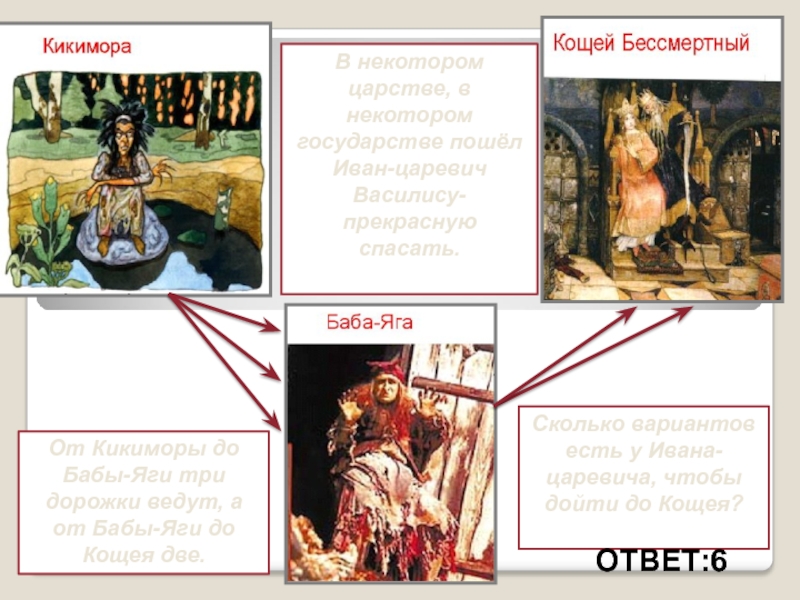
Слайд 14В некотором царстве, в некотором государстве пошёл Иван-царевич Василису- прекрасную
спасать.
От Кикиморы до Бабы-Яги три дорожки ведут, а от Бабы-Яги
до Кощея две.
Сколько вариантов есть у Ивана-царевича, чтобы дойти до Кощея?
Ответ:6
Слайд 15Пример:
На книжном стеллаже восемь полок. Книга может быть поставлена на
любую из них. Сколько информации содержит сообщение о том, где
находится книга?
Задаем вопросы:
- Книга лежит выше четвертой полки?
- Нет.
- Книга лежит ниже третьей полки?
- Да .
- Книга — на второй полке?
- Нет.
- Ну теперь все ясно! Книга лежит на первой полке!
Каждый ответ уменьшал неопределенность в два раза.
Всего было задано три вопроса. Значит набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
Слайд 16 Существует формула, которая связывает между собой количество возможных событий
и количество информации.
N = 2I ,где
N
— количество возможных вариантов,
I— количество информации.
Когда события равновероятны, количество информации о результате события (I, бит) и количество событий (N) связаны формулой: N=2I, вероятность: Р=1/N, N=1/P
Если из этой формулы выразить количество информации, то получится I = log2N (формула Хартли).
Слайд 17ЗАВИСИМОСТЬ МЕЖДУ количеством равновероятных событий (N) и количеством информации об
этом событии ( I )
Формула Хартли: I=log2N
N=2I
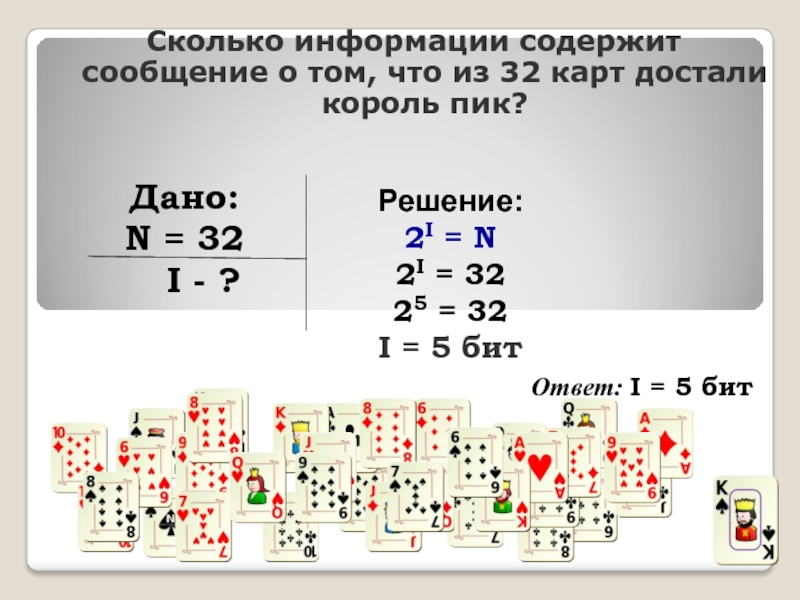
Слайд 18Сколько информации содержит сообщение о том, что из 32 карт
достали король пик?
Слайд 19КОЛИЧЕСТВО ВОЗМОЖНЫХ СОБЫТИЙ
И КОЛИЧЕСТВО ИНФОРМАЦИИ
Задача. В рулетке общее количество
лунок равно 128. Какое количество информации мы получим в зрительном
сообщении об остановке шарика в одной из лунок.
Слайд 20
В книге 512 страниц. Сколько информации несет сообщение о том,
что закладка лежит на какой-либо странице?
Слайд 21Сколько информации содержит сообщение о выпадении грани с числом 3
на шестигранном игральном кубике?
Слайд 22На экзамен приготовлено 20 билетов.
Чему равно количество событий, которые могут
произойти при вытягивании билета?
Равновероятны эти события или нет?
Чему
равна неопределенность знаний ученика перед тем как он вытянет билет?
Во сколько раз уменьшится неопределенность знания после того как ученик билет вытянул?
Зависит ли этот показатель от номера вытянутого билета?
Слайд 23Неравновероятные события
В жизни же мы сталкиваемся не только с
равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.
Например:
1.
Когда сообщают прогноз погоды, то сведения о том, что будет дождь, более вероятно летом, а сообщение о снеге — зимой.
2. Если вы — лучший ученик в группе, то вероятность сообщения о том,
что за контрольную работу вы получили 5, больше, чем вероятность получения двойки.
3. Если в мешке лежат 20 белых шаров и 5 черных, то вероятность достать черный шар меньше, чем вероятность вытаскивания белого.
Слайд 24Если N – это общее число возможных исходов какого-то процесса,
и из них интересующее нас событие может произойти К раз,
то вероятность этого события К/N.
Слайд 25Пример 1
В коробке имеются 50 шаров , из них 40
белых и 10 черных. Очевидно, вероятность того, что при вытаскивании
«не глядя» попадется белый шар, больше, чем попадания черного. Определить количественную вероятность для шаров каждого цвета.
Решение
Обозначим рч – вероятность попадания черного шара,
рб – вероятность попадания белого шара,
рч=10/50=0,2
рб =40/50 = 0,8.
Слайд 26Пример 2
Сережа - лучший ученик в группе. Вероятность того, что
за контрольную по математике он получит «5», больше, чем вероятность
получения «двойки». За год обучения Сережа получил 100 отметок. Из них: 60 пятёрок, 30 четверок, 8 троек и 2 двойки. Допуская, что данная тенденция сохранится и в будущем, вычислим вероятность получения каждой оценки.
Решение
Обозначим р5 – вероятность получения отметки «5»,
р4 – вероятность получения отметки «4»,
р3 – вероятность получения отметки «3»,
р2 – вероятность получения отметки «2»,
Тогда: р5=60/100=0,6
р4 =30/100 = 0,3
р3 = 8/100 = 0,03
р2 = 2/100 = 0,02.
Слайд 27Пример 3
В пруду живут 8 000 карасей, 2 000 щук
и 40 000 пескарей. Самая большая вероятность для рыбака –
поймать в этом пруду пескаря, на втором месте – карась, на третьем – щука. Определить с какой вероятностью будет поймана та или иная рыба.
Решение
8 000+2 000+40 000=50000 рыб в пруду.
рк=8000/50000=0,16
рщ =2000/50000 = 0,04
рп = 40000/50000 = 0,8.
Слайд 28Клод Э́лвуд Ше́ннон
30.04.1916 – 24.02.2001
американский математик и электротехник,
один из создателей математической теории информации.
Формулу для вычисления количества информации,
учитывающую неодинаковую вероятность событий, предложил К.Шеннон в 1948 году.
Слайд 29ФОРМУЛА ШЕННОНА
Среднее количество информации для событий с различными вероятностями определяется
по формуле:
Если события равновероятны ( pi=1/N ):
I – среднее количество
информации,
N – количество возможных событий
pi – вероятности отдельных событий
Количество информации для события с различными вероятностями определяется по формуле:
p – вероятность события
Слайд 30Количественная зависимость между вероятностью события (р) и количеством информации в
сообщении о нем (I) выражается формулой:
I = log 2 (1/p)
Слайд 31В корзине лежат 8 черных шаров и 24 белых. Сколько
информации несет сообщение о том, что достали черный шар?
Решение:
N =
8 + 24 = 32 – шара всего,
Рч = 8/32 = ¼ - вероятность доставания черного шара,
I = log2 (1/¼) = 2 бита.
Слайд 32Решение: Найдем общее количество рыб в озере: К = 12500
+ 25000 + 2*6250 = 50000.
Найдем вероятность попадания
на удочку
каждого вида рыб:
Ро = 12500/50000 = 0,25
Рк = 25000/50000 = 0,5
Pп = 6250/50000 = 0,125
Pщ = 6250/50000 = 0,125
Найдем количество информации:
I = - (0,25*log20,25 + 0,5*log20,5 + 0,125*log20,125 + 0,125*log20,125) бит ≈ 1,75 бита
В озере обитает 12500 окуней, 25000 пескарей, а карасей и щук по 6250. Сколько информации мы получим, когда поймаем какую - нибудь рыбу?
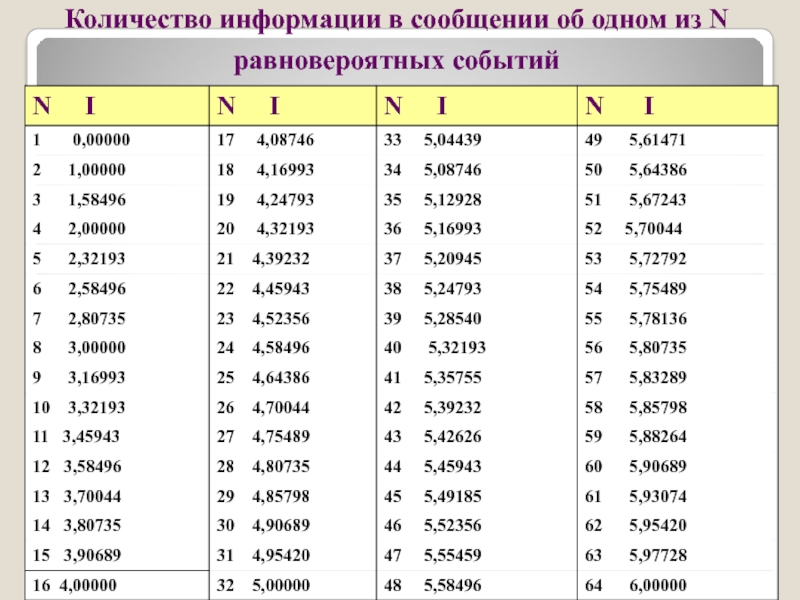
Слайд 33Количество информации в сообщении об одном из N равновероятных событий
Слайд 34ЗАДАНИЕ «БРОСАНИЕ ПИРАМИДКИ»
Определить количество информации, которую мы получим в результате
бросания несимметричной и симметричной пирамидок.
При бросании несимметричной четырехгранной пирамидки вероятности
отдельных событий равны:
Количество информации рассчитываем по формуле:
p1=1/2; p2=1/4; p3=1/8; p4=1/8.
I = (1/2·log21/2 + 1/4·log21/4 + 1/8·log21/8 + 1/8·log21/8) битов =
= (1/2·log22 + 1/4·log24 + 1/8·log28 + 1/8·log28) битов =
= (1/2 + 2/4+ 3/8+ 3/8) битов = 14/8 битов = 1,75 бита.
При бросании симметричной четырехгранной пирамидки вероятности отдельных событий равны между собой:
Количество информации рассчитываем по формуле:
p1= p2= p3= p4=1/4.
I = log24 = 2 бита.
Количество информации, которую мы получаем, достигает
максимального значения, если события равновероятны.