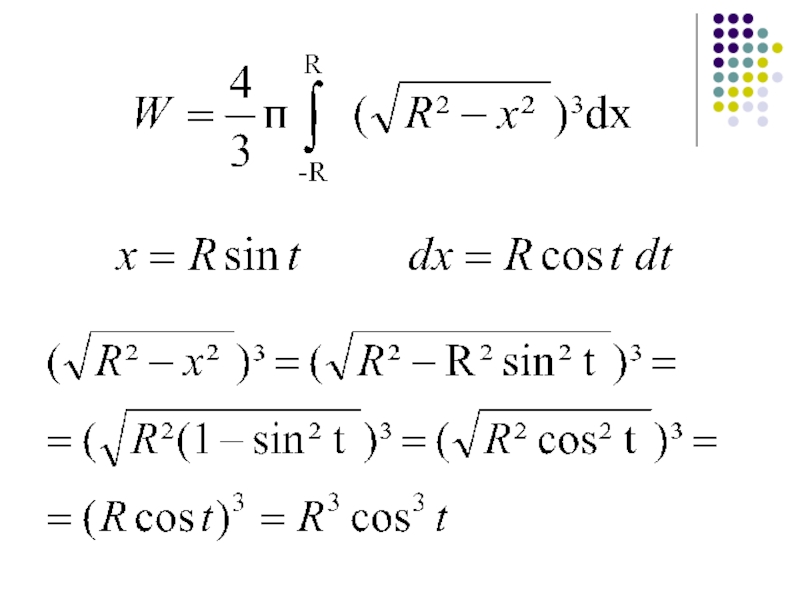Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гиперсфера
Содержание
- 1. Гиперсфера
- 2. Отражение в мозгу человека окружающего реального («объективного»)
- 3. Содержание Введение Основная часть Заключение Используемые ресурсы
- 4. Введение Четырехмерное пространствоМинковский и Эйнштейн
- 5. Цель: Интуитивно приблизиться к пониманию этой
- 6. Основная частьЧетырехмерное пространство Физический способ измерения размерности
- 7. Физический способ измерения размерностиx
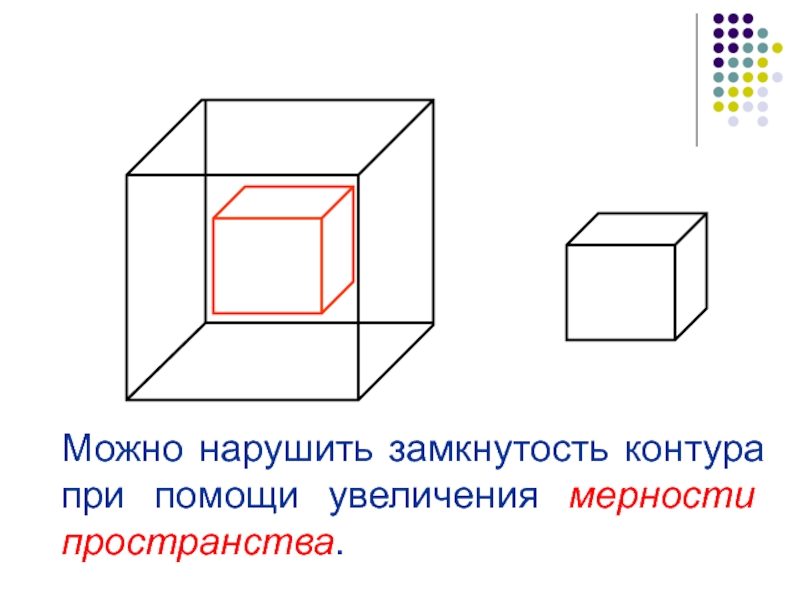
- 8. Можно нарушить замкнутость контура при помощи увеличения мерности пространства.
- 9. xyzИзменение симметрииВ пространстве размерности (n+1) можно менять симметрию объектов, взятых из пространства размерности n.
- 10. Слайд 10
- 11. Пространство с увеличением размерности n становится все более вместительным. Вместимость пространства
- 12. ГиперсфераRORO – центр гиперсферыR – радиус гиперсферыГиперсфера
- 13. Аналитическая модель гиперсферы А (x; y; z)B (x1;y1;z1)dyzxo
- 14. (x – x1) ² + (y –
- 15. (x – x1) ² + (y –
- 16. М – прямая, модель одномерного пространстваO –
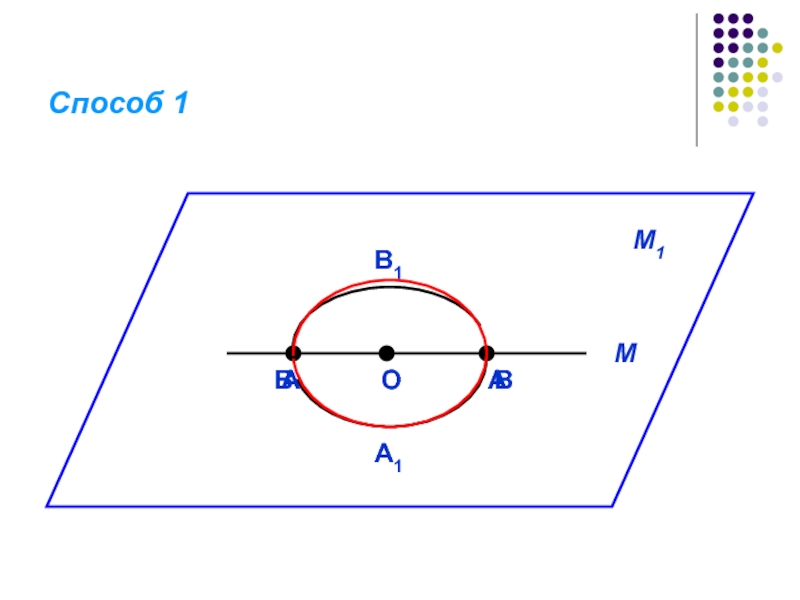
- 17. ОАВМВАM1B1A1Способ 1
- 18. Способ 1
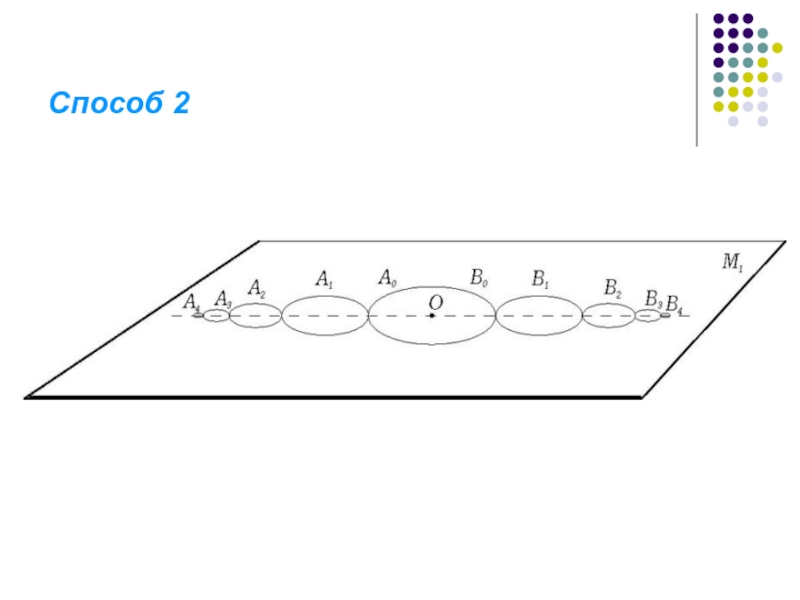
- 19. Способ 2
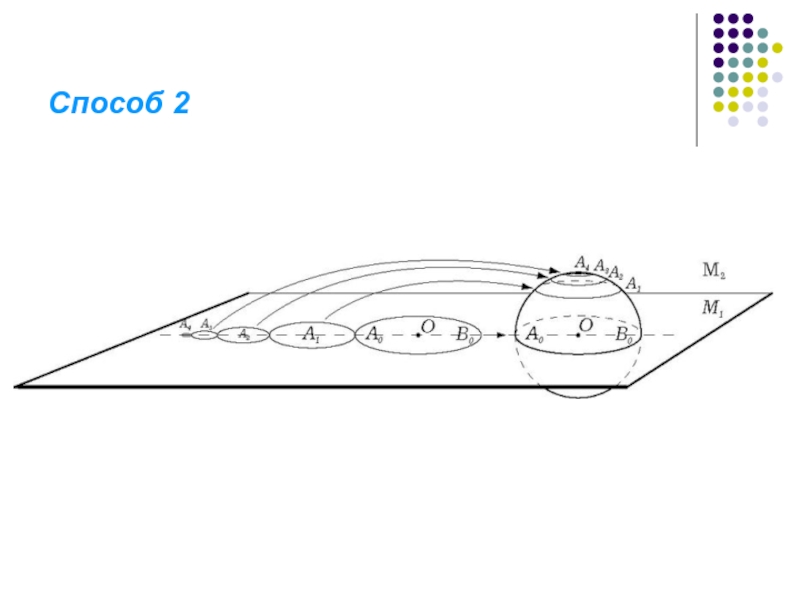
- 20. Способ 2
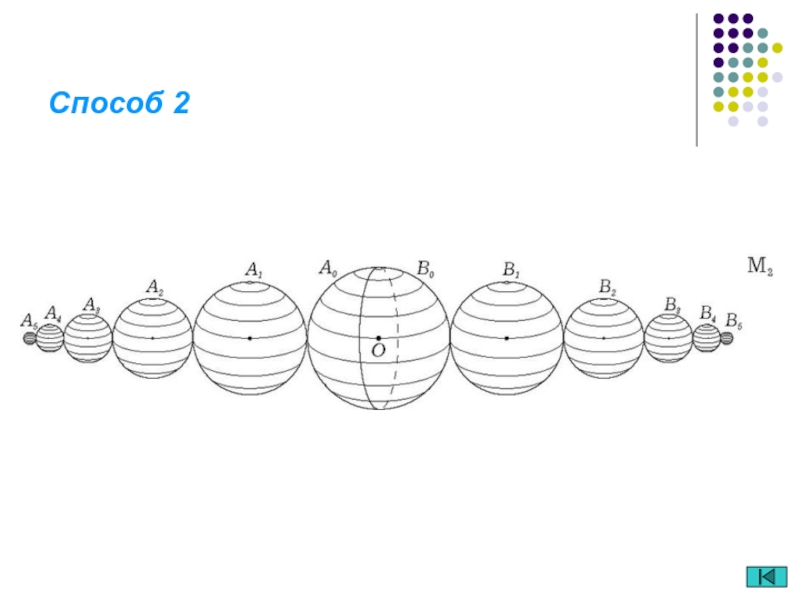
- 21. Способ 2
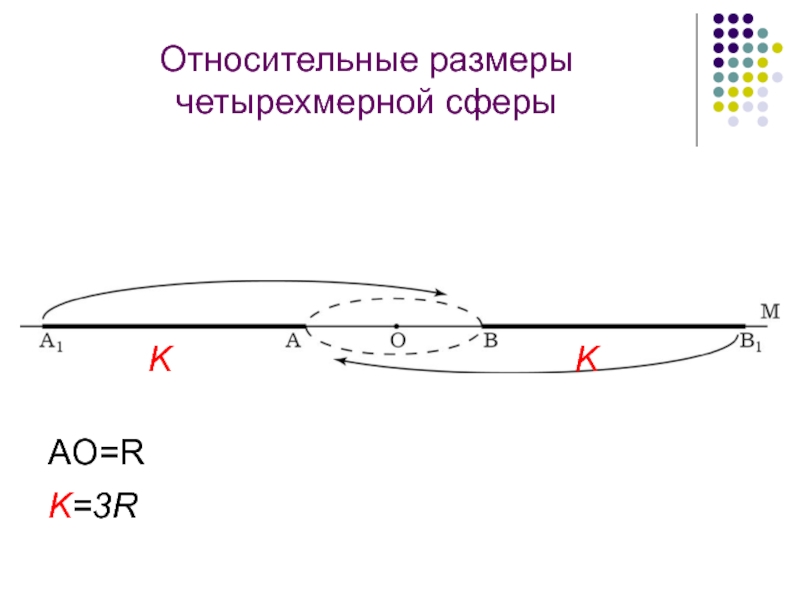
- 22. Относительные размеры четырехмерной сферы KKK=3RAO=R
- 23. Слайд 23
- 24. Слайд 24
- 25. O – центр гипершара, ГипершарOROХR – его
- 26. Гиперобъем гипершараТеорема.Если R – радиус гипершара,W – гиперобъем гипершара,тоДоказательство
- 27. xy-RRо
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Если R – радиус гипершара,V – объем
- 32. ТрехмернаяЧетырехмернаяСфераГиперсфераОбъемПлощадьS=4пR2V=2пR3ОбъемГиперобъем
- 33. Как видим, четырёхмерные фигуры можно изучать и
- 34. Список используемых ресурсовhttp://stratum.ac.ru/textbooks/kgrafic/lection16.htmlhttp://metaphysic.narod.ru/etud.htmhttp://fizika3000.narod.ru/prwr.htmhttp://ru.wikipedia.org/wiki Газета “Математика” приложение «1 сентября» 2005 г.
- 35. Скачать презентанцию
Отражение в мозгу человека окружающего реального («объективного») мира есть субъективное восприятие пространства человеком. Нарушение субъективных характеристик приводит к иллюзиям. Что такое размерность пространства и как узнать, какова размерность пространства, в котором
Слайды и текст этой презентации
Слайд 1Гиперсфера
п. Краснообск, 2008г.
Работу выполнил:
ученик 11б класса
Мартыненко Александр
Учитель:
Черемисина Г.
А.
Слайд 2Отражение в мозгу человека окружающего реального («объективного») мира есть субъективное
восприятие пространства человеком. Нарушение субъективных характеристик приводит к иллюзиям.
Что
такое размерность пространства и как узнать, какова размерность пространства, в котором мы живем? Согласно предложенной модели, наше пространство является четырехмерной сферой.
Отсюда следует насущная необходимость образного представления, если уж не самой сферы,
то хотя бы ее свойств.
Нижеследующие размышления имеют цель помочь читателю интуитивно приблизиться к пониманию этой геометрической формы.
Слайд 4 Введение
Четырехмерное пространство
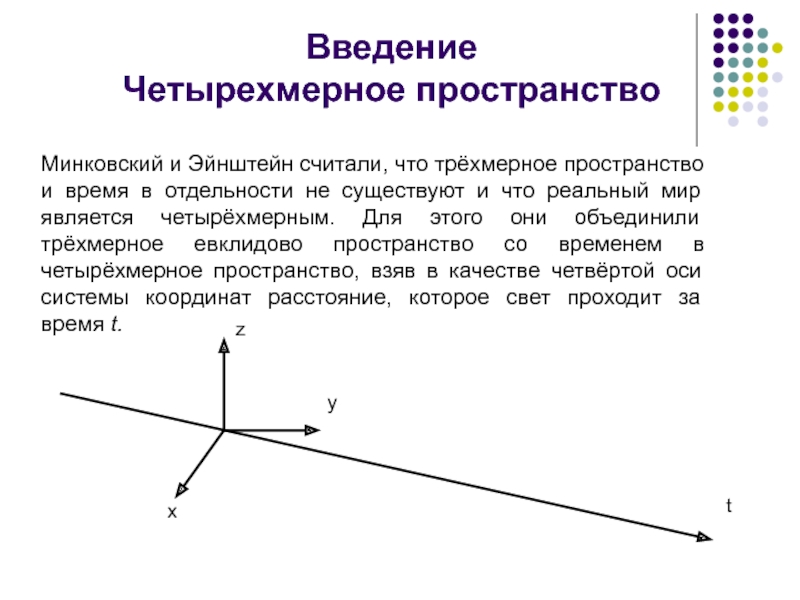
Минковский и Эйнштейн считали, что трёхмерное пространство
и время в отдельности не существуют и что реальный мир
является четырёхмерным. Для этого они объединили трёхмерное евклидово пространство со временем в четырёхмерное пространство, взяв в качестве четвёртой оси системы координат расстояние, которое свет проходит за время t.t
Слайд 5Цель:
Интуитивно приблизиться к пониманию этой геометрической формы гиперсферы
Дать первоначальное знакомство с четырёхмерным пространством на примере гиперсферы
(познакомится с определением гиперсферы, её уравнением и наглядным изображением). Для создания моделей четырёхмерных фигур в работе были использованы аналогии и закономерности фигур низших размерностей: точка, отрезок, окружность.
Слайд 6Основная часть
Четырехмерное пространство
Физический способ измерения размерности
Изменение симметрии
Вместимость
пространства
Гиперсфера
Определение
Способы представления гиперсферы
Аналитическая модель гиперсферы
Динамическая модель гиперсферы
Гипершар
Определение
Гиперобъем гипершара
Объем границы гипершара
Слайд 9x
y
z
Изменение симметрии
В пространстве размерности (n+1) можно менять симметрию объектов, взятых
из пространства размерности n.
Слайд 11
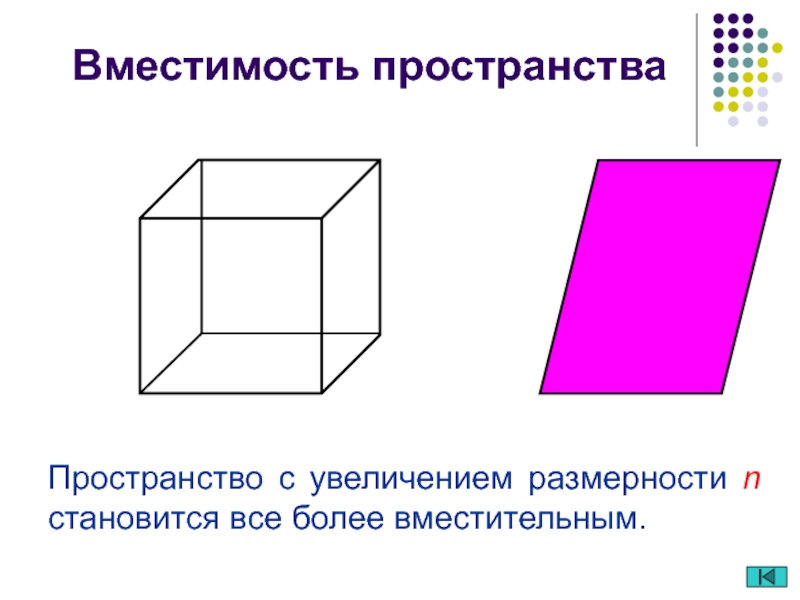
Пространство с увеличением размерности n становится все более вместительным.
Вместимость
пространства
Слайд 12Гиперсфера
R
O
R
O – центр гиперсферы
R – радиус гиперсферы
Гиперсфера – геометрическая фигура,
состоящая из всех точек четырехмерного пространства, расположенных на данном расстояние
от данных точек.
Слайд 16
М – прямая, модель одномерного
пространства
O – центр одномерной сферы
R
– радиус одномерной сферы
Способ 1
Динамическая модель гиперсферы
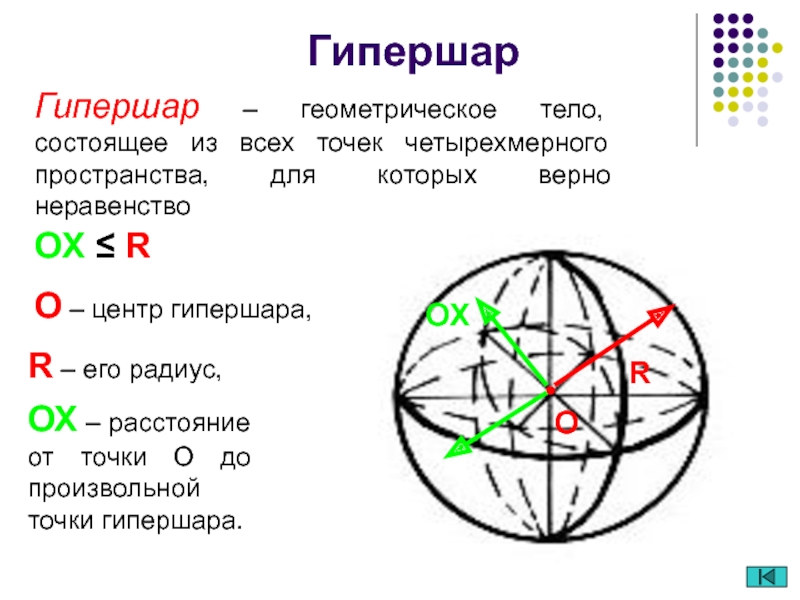
Слайд 25O – центр гипершара,
Гипершар
O
R
OХ
R – его радиус,
ОХ –
расстояние от точки О до произвольной точки гипершара.
OX ≤
RГипершар – геометрическое тело, состоящее из всех точек четырехмерного пространства, для которых верно неравенство
Слайд 26Гиперобъем гипершара
Теорема.
Если R – радиус гипершара,
W – гиперобъем гипершара,
то
Доказательство
Слайд 31Если R – радиус гипершара,
V – объем границы гиперсферы,
то
Объем границы
гиперсферы
n – количество гиперпирамид,
Vi – объем основания i-й гиперпирамиды,
hi –
высота i-й гиперпирамиды.
Слайд 33Как видим, четырёхмерные фигуры можно изучать и познавать так же,
как и трёхмерные, хотя в четырёхмерном пространстве существуют фигуры, аналогов
которых нет в пространствах низших размерностей.
Слайд 34Список используемых ресурсов
http://stratum.ac.ru/textbooks/kgrafic/lection16.html
http://metaphysic.narod.ru/etud.htm
http://fizika3000.narod.ru/prwr.htm
http://ru.wikipedia.org/wiki
Газета “Математика” приложение «1 сентября» 2005 г.
