Комбинаторика

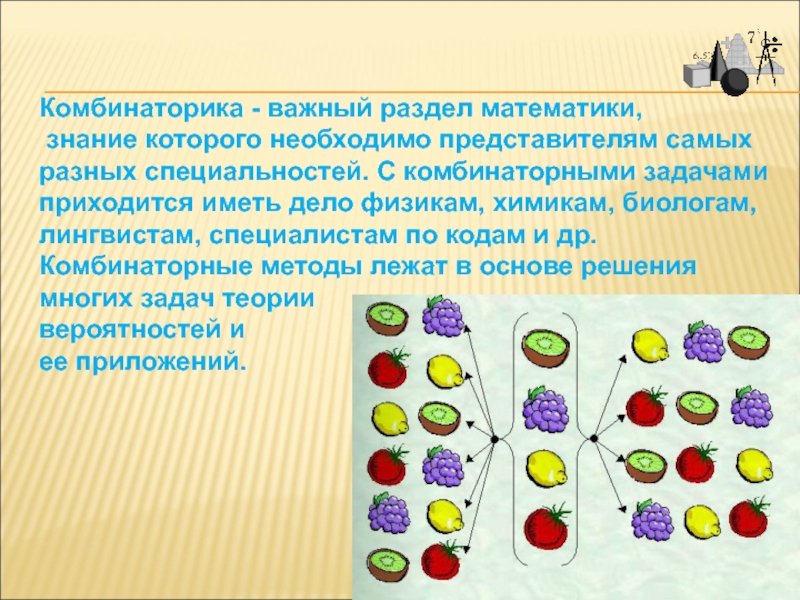
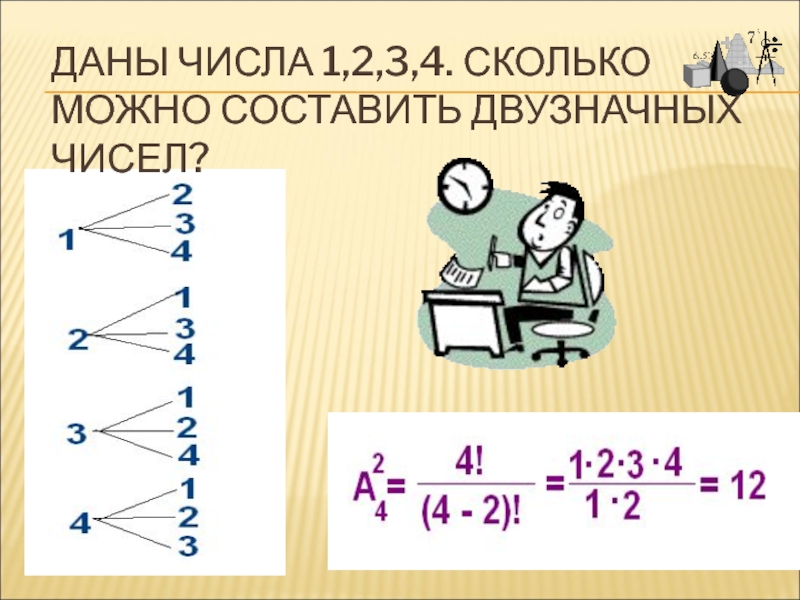
о том, сколько различных комбинаций, подчиненных тем или иным условиям,

можно составить из заданных объектов.
Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять».
Термин "комбинаторика" был введён знаменитым Готфридом Вильгельмом Лейбницем, - всемирно известным немецким учёным.

разных специальностей. С комбинаторными задачами приходится иметь дело физикам, химикам,

биологам, лингвистам, специалистам по кодам и др.
Комбинаторные методы лежат в основе решения многих задач теории
вероятностей и
ее приложений.

в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые

можно составить из частей и т.д.

Со временем появились различные игры
(нарды, карты, шашки, шахматы и т. д.)

В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.

(1.07.1646 - 14.11.1716)
Комбинаторику, как самостоятельный раздел математики первым

стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».

Леонард Эйлер(1707-1783)

рассматривал задачи о разбиении чисел, о паросочетаниях, циклических расстановках, о построении магических и латинских квадратов, положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку—топологию, которая изучает общие свойства пространства и фигур.

а другой объект В можно выбрать n способами, то выбор

«либо А, либо В» можно осуществить (m+n) способами.

При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В.

Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n - k) способов выбора, где k—число совпадений.

2 черных, 1 синий и 4 красных. Сколькими способами можно

взять из ящика цветной шар?
Решение:
Цветной шар – это синий или красный, поэтому применим правило суммы:

+

=

после каждого такого выбора объект В можно выбрать n способами,

то выбор пары (А,В) в указанном порядке можно осуществить mn способами.

При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

игральных костей?
Решение:
На первой кости может быть: 1,2,3,4,5 и 6 очков,

т.е. 6 вариантов.
На второй – 6 вариантов.
Всего: 6*6=36 вариантов.

Правила суммы и произведения верны для любого количества объектов.

дорог, а из города В в город С – 3

дороги. Сколькими способами можно проехать из города А в город С?

№2. На книжной полке стоят 3 книги по алгебре, 7 по геометрии и 2 по литературе. Сколькими способами можно взять с полки одну книгу по математике?


№3. В меню имеется 4 первых блюда, 3 – вторых, 2 – десерта. Сколько различных обедов можно из них составить?

обозначают n! и называют
«эн факториал»: n!=1•2•3•…•(n-1)•n.
2!=
1•2=
2
3!=
1•2•3=
6
4!=
1•2•3•4=
24
5!=
1•2•3•4•5=
6!=
120
1•2•3•4•5•6=
720
7!=
1•2•3•4•5•6•7=
5040
n!=(n-1)!•n
Удобная формула!!!

элементов, называются перестановками.
Обозначаются Рn


Перестановки

цифр.
1
159
195
5
9
519
591
915
951
2 комбинации



2 комбинации
2 комбинации
Всего 2•3=6 комбинаций.

и порядком, называются размещениями.

Размещения

сочетаниями из n -элементов по к.
Сочетания

можно сделать?

Решение:
Надо выбрать двух человек из 20.
Ясно, что

от порядка выбора ничего не зависит, то есть

Иванов - Петров или Петров - Иванов - это одна

и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.

если слова должны состоять: из 8 букв; из 7 букв;

из 3 букв?
2. Студенту необходимо сдать 4 экзамена в течение десяти дней. Сколькими способами можно составить ему расписание экзаменов?
3. Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?
4. Сколько существует различных автомобильных номеров, которые состоят из 5 цифр, если первая из них не равна нулю? Если номер состоит из одной буквы, за которой следуют четыре цифры, отличные от нуля?
5. Подрядчику нужны 4 плотника, а к нему с предложением своих услуг обратились 10. Сколькими способами он может выбрать среди них четверых?
6. Сколькими способами можно расставить на полке семь книг
7. Сколько 5-буквенных слов можно образовать, используя для этого 10 различных букв.
8. Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех лимонов и девяти апельсинов? (Фрукты одного вида считаем неразличимыми.)