Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока 7 класса
Содержание
- 1. Презентация для урока 7 класса
- 2. Цели:Введение понятия равенства геометрических фигур.Обучение сравнивать отрезки.Введение
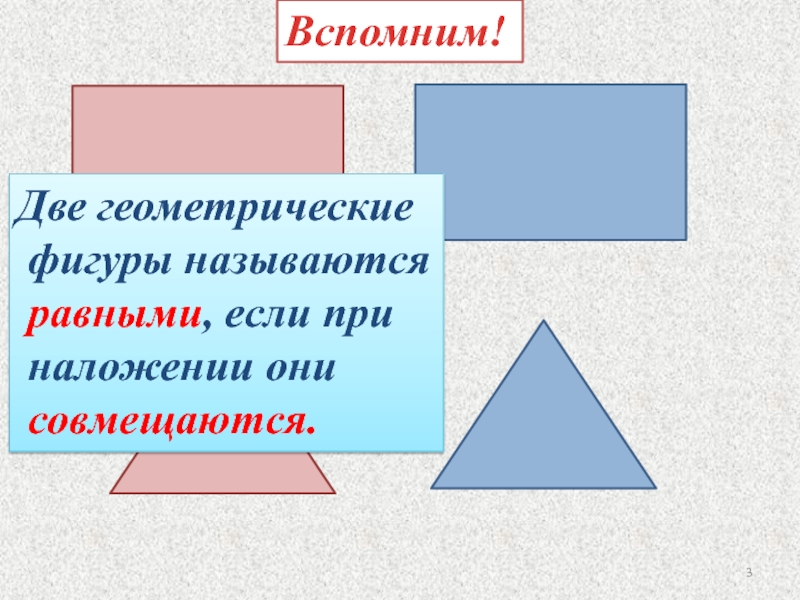
- 3. Вспомним!Две геометрические фигуры называются равными, если при наложении они совмещаются.
- 4. Если концы отрезков совпадают то отрезки АВ и СD равны. АВ = СD
- 5. Если концы отрезков не совпадают то отрезки
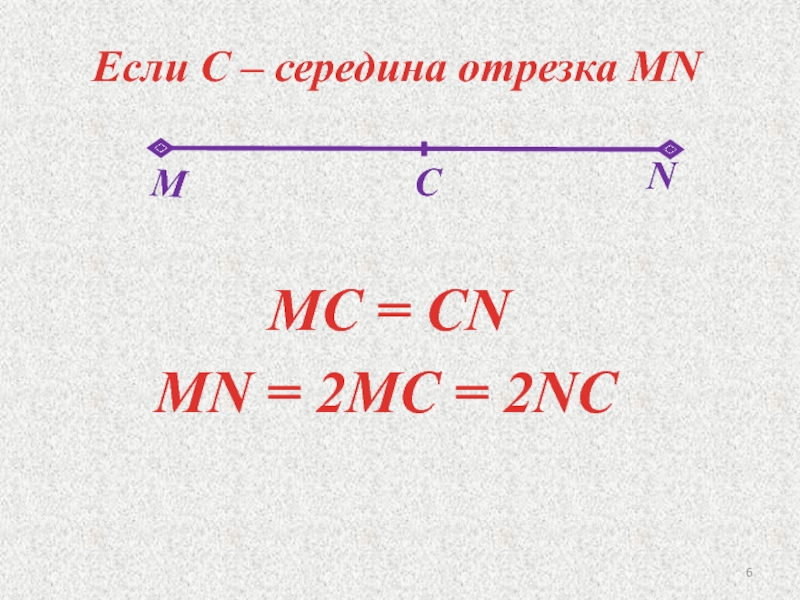
- 6. Если С – середина отрезка MNMC = СN MN = 2MC = 2NC
- 7. Если точка делит отрезок на два отрезка,
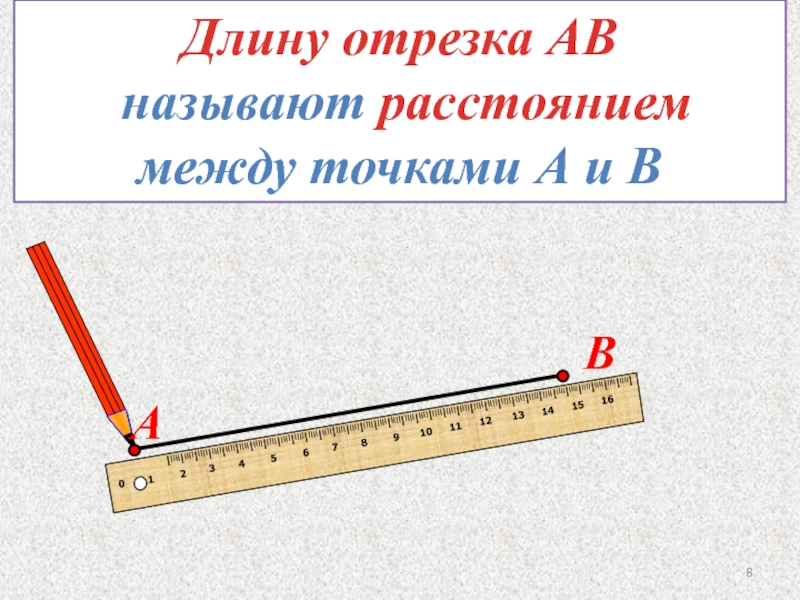
- 8. Длину отрезка АВ называют расстоянием между точками А и В
- 9. АВОЕ = 1 смАВ = 5 смДлину
- 10. 1 дм =10 см
- 11. Аршин – мера, возникшая при торговле с
- 12. Отметьте в тетради точки К и М.
- 13. А, В, С а, АВ =
- 14. В АС, АВ = 3,7
- 15. АВ = 64 см, С –
- 16. AF = FB, BK = KC,
- 17. О, А, В – лежат на
- 18. б) если точка О не лежит на
- 19. Ответить на вопросы:Какие геометрические фигуры называются равными?Какие
- 20. Скачать презентанцию
Цели:Введение понятия равенства геометрических фигур.Обучение сравнивать отрезки.Введение понятий: длины отрезка; свойства длин отрезков; единицы длины измерения отрезков.Решение задач на нахождение длины.
Слайды и текст этой презентации
Слайд 2Цели:
Введение понятия равенства геометрических фигур.
Обучение сравнивать отрезки.
Введение понятий: длины отрезка;
свойства длин отрезков; единицы длины измерения отрезков.
длины.
Слайд 7Если точка делит отрезок на
два отрезка, то длина всего
отрезка равна сумме длин этих
двух отрезков.
MN = MC +
CN 
Слайд 9А
В
ОЕ = 1 см
АВ = 5 см
Длину АВ измеряют расстоянием
между
точками А и В с помощью единичного отрезка
ОЕ –
единичный отрезок
Слайд 101 дм =10 см
1см = 10 мм
1 м =100см
1км = 1000мРусские меры длины.
Среди русских мер длины древнейшими являются локоть и сажень. Первое упоминание сажени встречается в летописи XI века.
Для измерения длины кроме сантиметра применяют и другие единицы длины
Слайд 11Аршин – мера, возникшая при торговле с народами Востока. Название
единицы происходит от персидского слова «арш», что значит локоть.
Сажень –
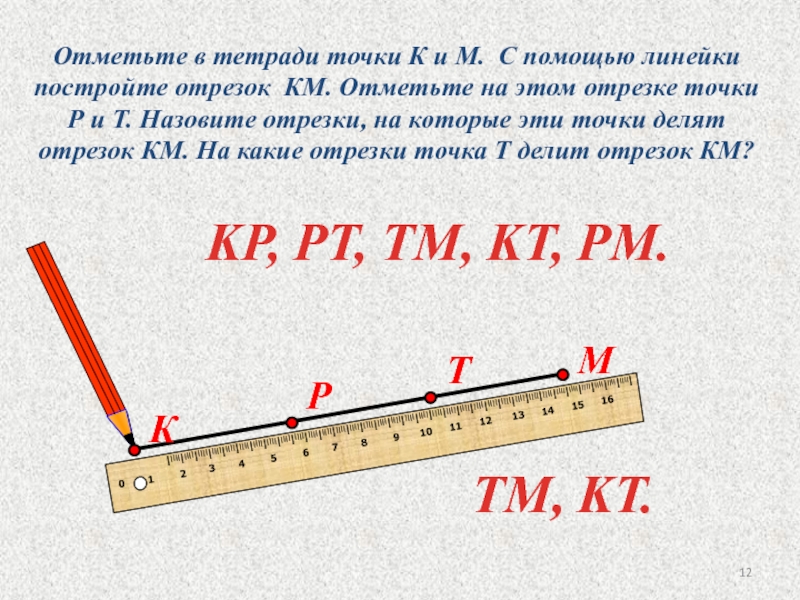
единица длины равная 3 аршинам. Кроме сажени, на Руси употреблялась косая сажень (2,48 м) и маховая (1,76 м).
Слайд 12Отметьте в тетради точки К и М. С помощью линейки
постройте отрезок КМ. Отметьте на этом отрезке точки Р и
Т. Назовите отрезки, на которые эти точки делят отрезок КМ. На какие отрезки точка Т делит отрезок КМ?KP, PT, TM, KT, PM.
TM, KT.
Слайд 13А, В, С а, АВ = 12 см, ВС
= 13,5 см
АС - ?
Решение
Возможны случаи:
а) точка В лежит между
А и С, тогда АС = АВ + ВС,АС = 12 + 13,5 = 25,5 (см).
б) точка А лежит между В и С, тогда АС = СВ - АВ,
АС = 13,5 - 12 = 1,5 (см).
Ответ: 25,5 см или 1,5 см.
Слайд 14 В АС, АВ = 3,7 см, АС =
7,2 см
ВС - ?
Решение
?
Так как В АС, АВ
+ ВС = АС,ВС = АС - АВ
ВС = 7,2 – 3,7 = 3,5 (см).
Ответ: BС = 3,5см.
Слайд 15 АВ = 64 см, С – середина АВ, D
- лежит
на луче СА, СD = 15 см.
ВD,
DA - ?Решение
АВ = 64 см, С – середина АВ, тогда АС = СВ = 32 см.
СD = 15 см, DA = AC – DC = 32 – 15 = 17 (см)
ВD = DC + CB = 15 + 32 = 47 (см)
Ответ: BD = 47см, DA = 17 см.
Слайд 16 AF = FB, BK = KC, AC = 5
см.
FK - ?
Решение
2FB + 2BK = 5 см, FB +
BK = 2,5 см,FB +BK = FK,
Поэтому FK = 2,5 см.
Ответ: FK = 2,5см.
По условию AF = FB, BK = KC, тогда
AF + FB + BK +KC = AC,
Слайд 17 О, А, В – лежат на одной прямой,
ОА =
12 см, ОВ = 9 см.
расстояние между серединами
отрезков ОА и ОВ - ?Решение
Пусть М – середина отрезка ОА, N – середина отрезка ОВ.
Возможны два случая:
а) если точка О лежит на отрезке АВ, то МО = АО : 2 = 6 см,
NO = BO : 2 = 4,5 см.
Расстояние между серединами отрезков ОА и ОВ равно
длине отрезка MN, a MN = MO + NO = 6 + 4,5 = 10,5 (см)
Слайд 18б) если точка О не лежит на отрезке АВ
б) если
точка О не лежит на отрезке АВ, то МО =
АО : 2 = 6 см,NO = BO : 2 = 4,5 см.
Пусть по условию: М – середина отрезка ОА, N – середина отрезка ОВ.
Решение
MN = MO – ON = 6 – 4,5 = 1,5 (см).
Ответ: а) 10,5 см; б) 1,5 см.
Слайд 19Ответить на вопросы:
Какие геометрические фигуры называются равными?
Какие отрезки равны?
Чему равна
длина отрезка?
Как измерить длину отрезка?
Какие есть единицы измерения длин?
