Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку "Классическое определение вероятности"
Содержание
- 1. Презентация к уроку "Классическое определение вероятности"
- 2. Теория вероятностей Развитие теории вероятностей с
- 3. Основатели теории вероятностей Основателями теории вероятностей
- 4. Блез Паскаль Род деятельности: математикматематик, философматематик, философ,
- 5. РЕБУС«СОБЫТИЕ»
- 6. СОБЫТИЕ это явление, которое происходит врезультате
- 7. ГОРИЗОНТАЛЬ1.А – «Буровая бригада бурит скважину №
- 8. ГОРИЗОНТАЛЬ2А – «Студент успешно сдал сессию»В – «Студент не сдал сессию»ПРОТИВОПОЛОЖНЫЕ
- 9. ГОРИЗОНТАЛЬ3. С помощью данной формулы:вычисляются РАЗМЕЩЕНИЯ
- 10. ГОРИЗОНТАЛЬ4.А – «В 2015 году будет освоена новая скважина на Федоровском месторождении»СЛУЧАЙНОЕ
- 11. ГОРИЗОНТАЛЬ4.А – «В 2015 году будет освоена новая скважина на Федоровском месторождении»СЛУЧАЙНОЕ
- 12. ВЕРТИКАЛЬ2.Соединения, которые отличаются друг от друга порядком расположения элементовПЕРЕСТАНОВКИ
- 13. ВЕРТИКАЛЬ5.А – «Оператор Иванов работает ЦДНГ(цех добычи
- 14. ВЕРТИКАЛЬ6.А – «Сессия когда – нибудь закончится»ДОСТОВЕРНОЕ
- 15. ВЕРТИКАЛЬ7.Это действие в комбинаторике обозначают восклицательным знаком.ФАКТОРИАЛ
- 16. ВЕРТИКАЛЬ8. А – «Планируемый показатель дебита скважины
- 17. ВЕРТИКАЛЬ9.Соединения, которые отличаются друг от друга хотя бы одним элементом.СОЧЕТАНИЯ
- 18. ВЕРТИКАЛЬ10.Плох тот студент, который не мечтает видеть эту цифру в своей зачетке. ПЯТЬ
- 19. Слайд 19
- 20. наступления этого события равна Вероятность
- 21. Доводы, докоторыхчеловекдодумалсясам, обычноубеждаютего больше,нежелите, которыепришли вголову другими.
- 22. ЭКЗАМЕНЫ
- 23. В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:«Вероятность – возможностьисполнения,осуществимости чего-нибудь».ВЕРОЯТНОСТЬ
- 24. Вероятность – это числоваяхарактеристикавозможностипоявления какоголибоопределенногособытия в тех илииныхусловиях, которыемогутповторятьсянеограниченноечисло раз.Основатель современной теории вероятностей А.Н.Колмогоров:
- 25. ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ
- 26. P – обозначение происходит от первойбуквы французского слова probabilite – вероятность.
- 27. А –событие достоверноеР(А) = 1А – событие
- 28. Пьер-Симо́н Лапла́с Классическоеопределениевероятностибыловпервые дано вработахфранцузскогоматематикаЛапласа.
- 29. РЕБУС«исход»
- 30. ОШИБКА ДАЛАМБЕРА Жан Лерон ДаламберКаковавероятность, что подброшенные
- 31. В ходе данного испытания могут быть такие
- 32. В ходе данного испытания могут быть такие
- 33. Тогда всего исходов n = 4 благоприятных
- 34. математическое Добро пожаловать в
- 35. 23456789101112131415161
- 36. Задача № 1 Среди 125 КНС разыгрываетсяприз. Какова вероятность, чтономер победившей КНС будетзаканчиваться на тройку?
- 37. На семи одинаковых карточках разрезной азбуки буквы:
- 38. Задача № 3 Вероятность запуска насоса после
- 39. Задача № 4 Значением показаний манометра (
- 40. Из 60 экзаменационных вопросов студент подготовил 50.
- 41. Задача № 6 Из полного набора домино
- 42. Подведём итоги !
- 43. Это короткое литературное произведение, характеризующее предмет (тему),
- 44. ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА1 строчка – одно слово
- 45. Теория вероятностей. Новая, интересная. Изучим, поймем, заинтересуемся.
- 46. Скачать презентанцию
Теория вероятностей Развитие теории вероятностей с момента зарождения этой науки и до настоящего времени было несколько своеобразным. На первом этапе истории этой науки она рассматривалась как занимательный “пустячок”, как собрание
Слайды и текст этой презентации
Слайд 3Основатели теории вероятностей
Основателями теории вероятностей были французские математики
Б. Паскаль и П. Ферма, и голландский ученый Х. Гюйгенс
Б. Паскаль
П.Ферма
Х. Гюйгенс
Слайд 4
Блез Паскаль
Род деятельности: математикматематик, философматематик, философ, литераторматематик, философ, литератор,
физик
Дата рождения:19 июня19 июня 1623
Место рождения: Клермон-ФерранКлермон-Ферран, ОверньКлермон-Ферран, Овернь, Франция
Дата смерти:19 августа19 августа 1662
(39 лет)Место смерти: ПарижПариж, Франция
СЛУЧАЙНЫЕ ОТКРЫТИЯ ДЕЛАЮТ ТОЛЬКО ПОДГОТОВЛЕННЫЕ УМЫ
Слайд 6СОБЫТИЕ
это явление, которое происходит в
результате осуществления каких -
либо
условий
ПРИМЕР. Бросаем шестигранный игральный кубик.
А {выпало четное число очков};В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.
✔
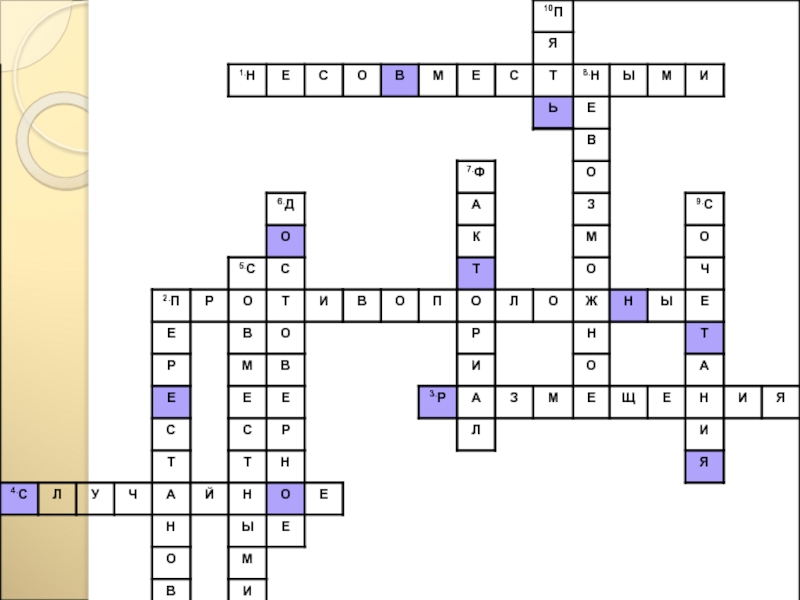
Слайд 7ГОРИЗОНТАЛЬ
1.
А – «Буровая бригада бурит скважину № 5 на Федоровском
месторождении»
В – «Эксплуатационная бригада, производит добычу нефти из скважины №
5 на Федоровском месторождении» НЕСОВМЕСТНЫМИ
Слайд 10ГОРИЗОНТАЛЬ
4.
А – «В 2015 году будет освоена новая скважина на
Федоровском месторождении»
СЛУЧАЙНОЕ
Слайд 11ГОРИЗОНТАЛЬ
4.
А – «В 2015 году будет освоена новая скважина на
Федоровском месторождении»
СЛУЧАЙНОЕ
Слайд 12ВЕРТИКАЛЬ
2.
Соединения, которые отличаются друг от друга порядком расположения элементов
ПЕРЕСТАНОВКИ
Слайд 13ВЕРТИКАЛЬ
5.
А – «Оператор Иванов работает ЦДНГ(цех добычи нефти и газа)
№ 5 Федоровскнефть»
В – «Оператор Иванов является студентом СНТ»
СОВМЕСТНЫМИ
Слайд 16ВЕРТИКАЛЬ
8.
А – «Планируемый показатель дебита скважины №2 Федоровского месторождения
на 30 февраля 2015 г. составит 50 тонн»
НЕВОЗМОЖНОЕ
Слайд 21Доводы, до
которых
человек
додумался
сам, обычно
убеждают
его больше,
нежели
те, которые
пришли в
голову другими.
Слайд 23В толковом словаре
С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность –
возможность
исполнения,
осуществимости
чего-нибудь».
ВЕРОЯТНОСТЬ
Слайд 24Вероятность – это
числовая
характеристика
возможности
появления какого
либо
определенного
события в тех или
иных
условиях, которые
могут
повторяться
неограниченное
число раз.
Основатель
современной
теории вероятностей
А.Н.Колмогоров:
Слайд 25ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ ВЕРОЯТНОСТИ СОБЫТИЯ:
А
– некоторое событие,
m – количество исходов благоприятствующих появлению события А
n
– количество исходов этого событияВероятностью наступления случайного события А называется отношение
Слайд 27А –событие достоверное
Р(А) = 1
А – событие невозможное
Р(А) =
0
Вероятность наступления случайного события больше или равна нулю, но меньше
или равна единице: 0 ≤ P (A) ≤ 1
Слайд 28Пьер-Симо́н Лапла́с
Классическое
определение
вероятности
было
впервые дано в
работах
французского
математика
Лапласа.
Слайд 30ОШИБКА ДАЛАМБЕРА
Жан Лерон Даламбер
Какова
вероятность, что подброшенные вверх две монеты
упадут на одну
и ту же сторону?
Слайд 31В ходе данного испытания могут быть такие исходы:
1. Обе монеты
упали на «орла»
2. Обе монеты упали на «решку»
3. Одна
из монет упала на «орла», другая на «решку»Р (А) =
РЕШЕНИЕ ДАЛАМБЕРА
Слайд 32В ходе данного испытания могут быть такие исходы:
1. Первая монета
упала на «орла», вторая тоже на «орла»
2. Первая монета упала
на «решку», вторая тоже на «решку»3. Первая монета упала на «орла», а вторая – на «решку»
4. Первая монета упала на «решку», а вторая – на «орла»
ПРАВИЛЬНОЕ РЕШЕНИЕ
Слайд 33Тогда всего исходов n = 4
благоприятных m = 2
И вероятность
события будет
Р(А) =
помните,
что природа различает все предметы,
даже если внешне они для нас неотличимы.
Слайд 36
Задача № 1
Среди 125 КНС разыгрывается
приз. Какова вероятность, что
номер
победившей КНС будет
заканчиваться на тройку?
Слайд 37
На семи одинаковых карточках
разрезной азбуки буквы:
«А», «О», «Э»,
«Г», «Н», «Р», «М».
Наудачу выбрали пять карточек и
положили
их в ряд в порядке их извлечения. Какова вероятность
получить при этом слово «РЭНГМ».
Задача № 2
Слайд 38
Задача № 3
Вероятность запуска насоса после ремонта равна 0,95
%.
Произвели 55 попыток запуска.
найдите ожидаемое число
неудачных запусков.
Слайд 39
Задача № 4
Значением показаний манометра
( прибор для измерения
давления)
может быть любое двузначное число.
Какова вероятность того, что
наугад выбранный результат
состоит из одинаковых цифр.
Слайд 40
Из 60 экзаменационных вопросов
студент подготовил 50.
На экзамене он
должен
ответить на два вопроса.
Какова вероятность того,
что студент
ответит на оба вопроса?
Задача № 5
Слайд 41
Задача № 6
Из полного набора домино
извлекается наудачу
одна
кость.
Какова вероятность того,
что число
очков в ней четное.
Слайд 43Это короткое литературное
произведение,
характеризующее
предмет (тему),
состоящее из пяти
строк,
которое пишется по
определённому плану.
Синквейн
Слайд 44ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА
1 строчка – одно слово – название стихотворения,
тема, обычно существительное.
2 строчка – два слова (прилагательные или причастия).
Описание темы, т.е какая это тема для нас, слова можно соединять союзами и предлогами.3 строчка – три слова (глаголы). Действия, относящиеся к теме (которые мы произведем)
4 строчка – четыре слова – предложение. Фраза, которая показывает значимость темы.
5 строчка – одно слово – ассоциация, синоним, который повторяет суть темы (для чего может использоваться, чем быть)
Слайд 45Теория вероятностей.
Новая, интересная.
Изучим, поймем, заинтересуемся.
Присутствует во всех областях.
Инструмент познания.
Истинная логика
нашего
мира – правильный
подсчет вероятностей.
(Джеймс Максвелл)
