Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная. Гапонов Д.С.
Содержание
- 1. Производная. Гапонов Д.С.
- 2. Определение производной
- 3. Геометрический смысл производной
- 4. Физический смысл, диффиринцируемость
- 5. Слайд 5
- 6. Дифферинцирование функции.Сложная производная. Примеры
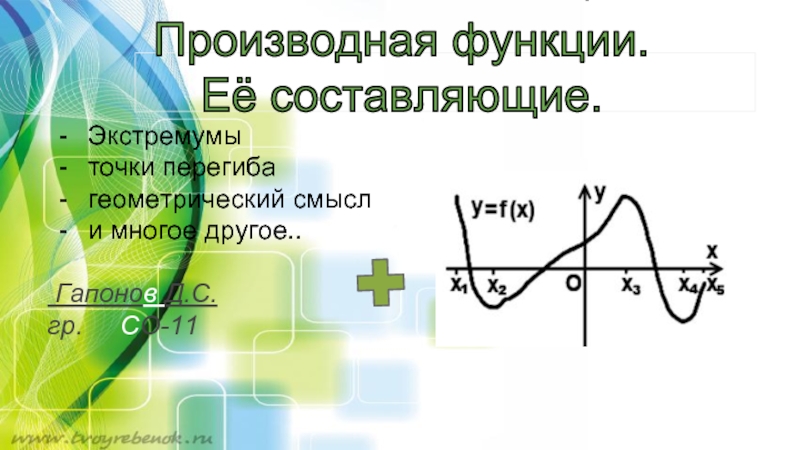
- 7. Основные понятия : критические точки, экстремумы, тд.
- 8. Точки перегиба, выпуклость и вогнутостьВыпуклую вверх функцию
- 9. Точки перегибаОпределение точки перегибаРассмотрим функцию y=f(x), которая
- 10. Сподіваюся, що вам сподобалосяМиру вам)))The end.
- 11. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5
Дифференцирование функции
При решении задач дифференцирования приходится искать производные функций различных классов. Мы рассмотрим основные правила дифференцирования, которые используем при нахождении производных. Обязательно остановимся на подробном решении примеров, чтобы понять принцип их применения.
Слайд 7Основные понятия : критические точки, экстремумы, тд. и зачем мы
исследуем
Зачем исследовать функцию с помощью производной?
Чтобы лучше узнать, как выглядит
график этой функции: где он идёт «снизу вверх», где «сверху вниз», где достигает минимумов максимумов (если вообще достигает). Не все функции такие простые – в большинстве случаев у нас вообще нет ни малейшего представления о графике той или иной функции. Критическими точками функции называют внутренние точки области определения, в которых производная функции равна нулю или не существует.
Слайд 8Точки перегиба, выпуклость и вогнутость
Выпуклую вверх функцию часто называют выпуклой,
а выпуклую вниз – вогнутой.
Посмотрите на чертеж, иллюстрирующий эти определения,
он слева.Слайд 9Точки перегиба
Определение точки перегиба
Рассмотрим функцию y=f(x), которая является непрерывной в
точке x0. Функция f(x) может иметь в этой точке конечную
или бесконечную производную f′(x0). Если при переходе через x0 функция меняет направление выпуклости, т.е. существует число δ>0, такое, что на одном из интервалов (x0−δ,x0) или (x0,x0+δ) функция является выпуклой вверх, а на другом − выпуклой вниз, то x0называется точкой перегиба функции y=f(x).Геометрический смысл точки перегиба состоит в том, что график функции f(x) переходит в этой точке с одной стороны касательной на другую, т.е. кривая и касательная взаимно пересекаются
(рисунок 1).
Другое интересное свойство точки перегиба состоит в том, что график функции f(x) в окрестности точки перегиба x0 расположен внутри одной пары вертикальных углов, образованных касательной и нормалью (рисунок 2).
Необходимое условие существования точки перегиба
Если x0 − точка перегиба функции f(x) и данная функция имеет вторую производную в некоторой окрестности точки x0, причем в точке x0 она непрерывна, то
f′′(x0)=0.
Пример решения задачи на обнаружения перегиба и выпуклостей