Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прототип В14. Исследование сложной функции, содержащей показательную, логарифмическую функции и функцию квадратный корень 11 класс
Содержание
- 1. Прототип В14. Исследование сложной функции, содержащей показательную, логарифмическую функции и функцию квадратный корень 11 класс
- 2. Первый способ (традиционный) предполагает использование алгоритмов и
- 3. Алгоритм нахождения наибольшего (наименьшего) значения функции без
- 4. Алгоритм нахождения точек экстремума.Найти производную функции.Приравнять производную
- 5. Формулы:Дифференцирование показательной функции:Дифференцирование логарифмической функции:Дифференцирование сложной функции:
- 6. 245180 Найдите наибольшее значение функции
- 7. 245184 Найдите наибольшее значение функции
- 8. Не очень просто.Тем более, что некоторые программы
- 9. В случае, если мы имеем дело со
- 10. Функция
- 11. Можно и совсем обойтись без производной.Используем простые графические соображения.
- 12. Функция
- 13. Функция
- 14. Решим таким же способом
- 15. Функция
- 16. Функция
- 17. Реши самостоятельно любым способом:Найдите точку минимума функции
- 18. Источник:Открытый банк задач ЕГЭ
- 19. Скачать презентанцию
Первый способ (традиционный) предполагает использование алгоритмов и знание формул.Алгоритм нахождения наибольшего (наименьшего) значения функции на промежутке :Найти производную функции.Приравнять производную к нулю и решить полученное уравнение.Найти значение функции на краях числового
Слайды и текст этой презентации
Слайд 1Прототипы В 14 Исследование сложной функции, содержащей показательную, логарифмическую функции
и функцию квадратный корень.
Татьяна Александровна
Слайд 2Первый способ (традиционный) предполагает использование алгоритмов и знание формул.
Алгоритм нахождения
наибольшего (наименьшего) значения функции на промежутке :
Найти производную функции.
Приравнять производную
к нулю и решить полученное уравнение.Найти значение функции на краях числового промежутка и в нулях производной, входящих в данный числовой промежуток.
Выбрать среди полученных значений функции значение, соответствующее вопросу задачи (наибольшее или наименьшее)
Важно: промежуток может быть не указан, но очевиден: область определения.
Слайд 3Алгоритм нахождения наибольшего (наименьшего) значения функции без указания числового промежутка:
Найти
производную функции.
Приравнять производную к нулю и решить полученное уравнение.
Провести исследование
на эстремумы на области определения функции. Если эстремум один, то именно в нем достигается наибольшее (наименьшее) значение функции.Найти соответствующее значение функции, подстановкой.
Слайд 4Алгоритм нахождения точек экстремума.
Найти производную функции.
Приравнять производную к нулю и
решить полученное уравнение.
На числовой прямой отметить нули производной и точки,
в которых производная не определена.Соотнести поведение производной с поведением функции и ответить на вопрос.
Например:
Ответ:
Слайд 5Формулы:
Дифференцирование показательной функции:
Дифференцирование логарифмической функции:
Дифференцирование сложной функции:
Слайд 6245180 Найдите наибольшее значение функции
.
Решение:
Промежуток не указан. Очевидно, что необходимо исследовать функцию на всей области определения.
Ответ:
Конечно, страшновато, но
уже ясно, что краев у
числового промежутка нет,
а, следовательно в них не будет достигаться наибольшее или наименьшее значение.
Убедимся, что это наибольшее значение:
Точка максимума одна, следовательно в ней и будет
наибольшее значение.
Слайд 7245184 Найдите наибольшее значение функции
.
Решение:
Ответ:
Промежуток не указан.
Очевидно, что необходимо исследовать функцию на всей области определения.Разделим на первый и второй множители,
не равные нулю:
Убедимся, что это наибольшее значение:
т. max
Точка максимума одна, следовательно в ней и будет
наибольшее значение.
Слайд 8Не очень просто.
Тем более, что некоторые программы не предусматривают использование
формул дифференцирования показательной и логарифмической функции в общем виде.
Попробуем иначе.
Без использования алгоритма и формул.
Слайд 9В случае, если мы имеем дело со сложной функцией f(g(x)),
где f – монотонная функция, то достаточно исследовать функцию g(x).
Наибольшие, наименьшие значения, точки экстремума функция f будет иметь такие же, что и функция g(x). Конечно, с учетом области определения.
Слайд 10Функция
возрастает на R, следовательно наибольшее значение принимает при наибольшем значении
аргумента (аргументом в данном случае является функция, находящаяся в показателе).245184
Найдите наибольшее значение функции .
Решение:
Исследуем на наибольшее значение функцию, находящуюся в показателе.
Следовательно
т. max
Следовательно
Ответ:
Слайд 12Функция
возрастает на R, следовательно наименьшее значение принимает при наименьшем значении
аргумента (функции, находящейся в показателе).245183
Найдите наименьшее значение функции
Решение:
Исследуем на наибольшее значение функцию, находящуюся в показателе.
Следовательно
Ответ:
График – парабола, ветви направлены
вверх.
Слайд 13Функция
возрастает на всей области определения
, следовательно наибольшее значение принимает при наибольшем значении значении аргумента (функции, находящейся под знаком логарифма).245180
Найдите наибольшее значение функции .
Решение:
Исследуем на наибольшее значение функцию, находящуюся под знаком логарифма.
Следовательно
Ответ:
График – парабола, ветви направлены
вниз.
Слайд 14 Решим таким же способом задания, связанные с
исследованием сложной функции, содержащей квадратичную функцию под знаком квадратного корня.
Слайд 15Функция
возрастает на всей области определения,
следовательно ведет себя так же, как подкоренная функция на области определения.245174
Найдите точку минимума функции .
Решение:
Исследуем функцию, находящуюся под знаком корня.
Ответ:
График – парабола, ветви направлены
вверх.
Подкоренное выражение больше нуля при любом значении х. D(y):R.
Слайд 16Функция
возрастает на всей области определения,
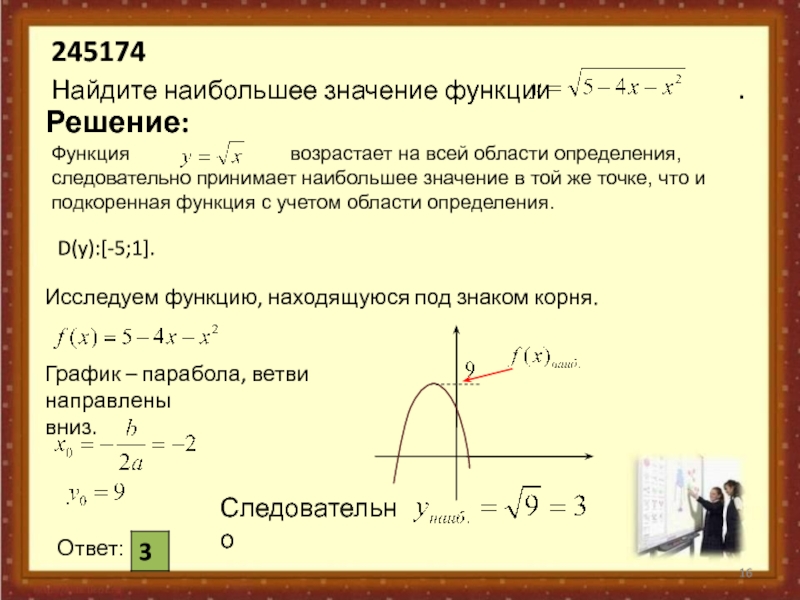
следовательно принимает наибольшее значение в той же точке, что и подкоренная функция с учетом области определения.245174
Найдите наибольшее значение функции .
Решение:
Исследуем функцию, находящуюся под знаком корня.
Ответ:
График – парабола, ветви направлены
вниз.
D(y):[-5;1].
Следовательно
Слайд 17Реши самостоятельно любым способом:
Найдите точку минимума функции
.
Найдите точку максимума функции .
Найдите наименьшее значение функции
Найдите наименьшее значение функции .
