Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Центральная и осевая симметрия.
Содержание
- 1. Центральная и осевая симметрия.
- 2. ОглавлениеЦентральная симметрия Осевая симметрияЗаключение
- 3. ОпределениеСимметрия (от греч. Symmetria – соразмерность), в
- 4. Центральная симметрияДве точки А и А1 называются
- 5. Построение точки, центрально-симметричной даннойАПостроить луч АОИзмерить длину
- 6. Построение отрезка, центрально-симметричного данномуПостроить луч АОИзмерить длину
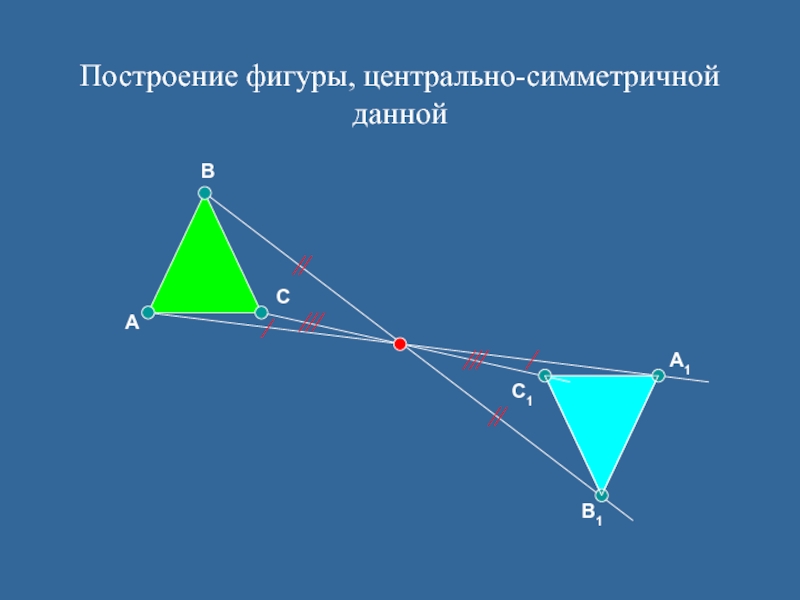
- 7. Построение фигуры, центрально-симметричной даннойАВСОА1В1С1Центрально-симметричные фигуры равны
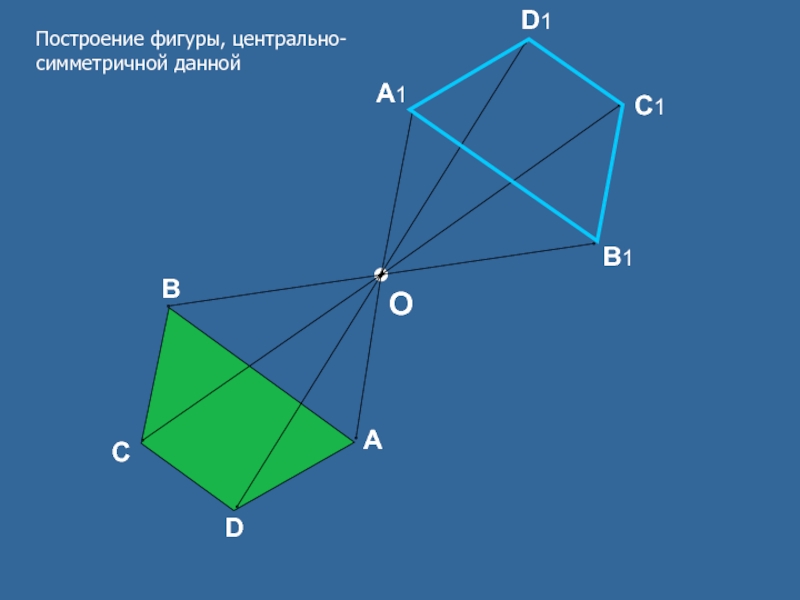
- 8. BACDB1A1C1D1OПостроение фигуры, центрально-симметричной данной
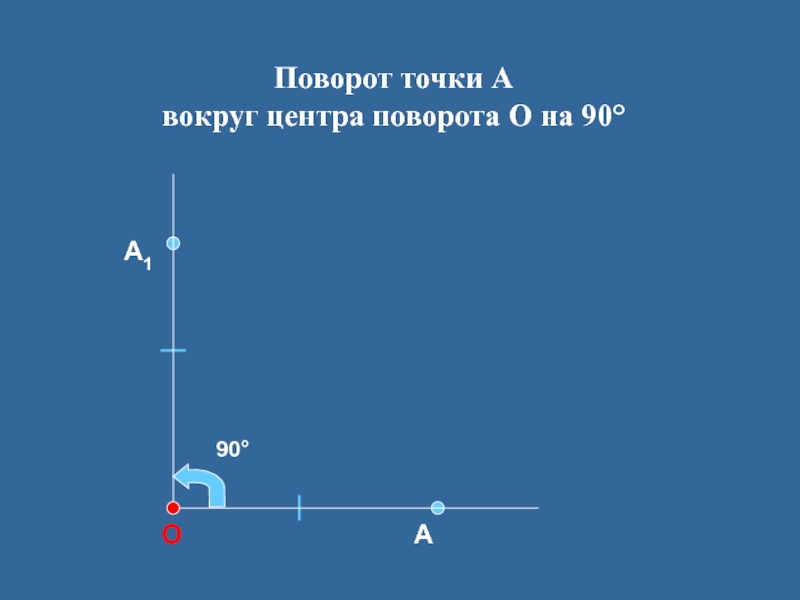
- 9. Поворот точки А вокруг центра поворота О на 90°
- 10. Повороты точек на различные углыОАА1А2А345°90°135°
- 11. Фигуры, имеющие центр симметрии:
- 12. Осевая симметрияПреобразование фигуры F в фигуру F1,
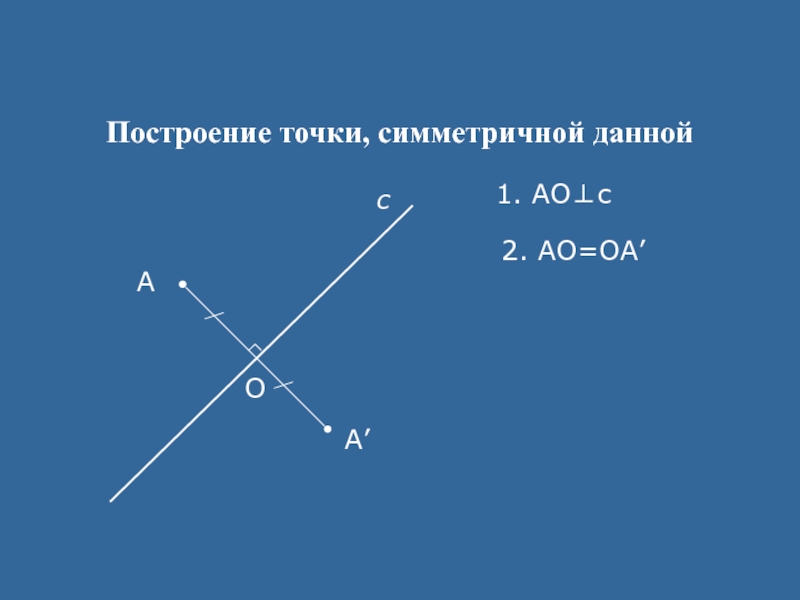
- 13. Построение точки, симметричной даннойАсА’1. АО⊥сО2. АО=ОА’
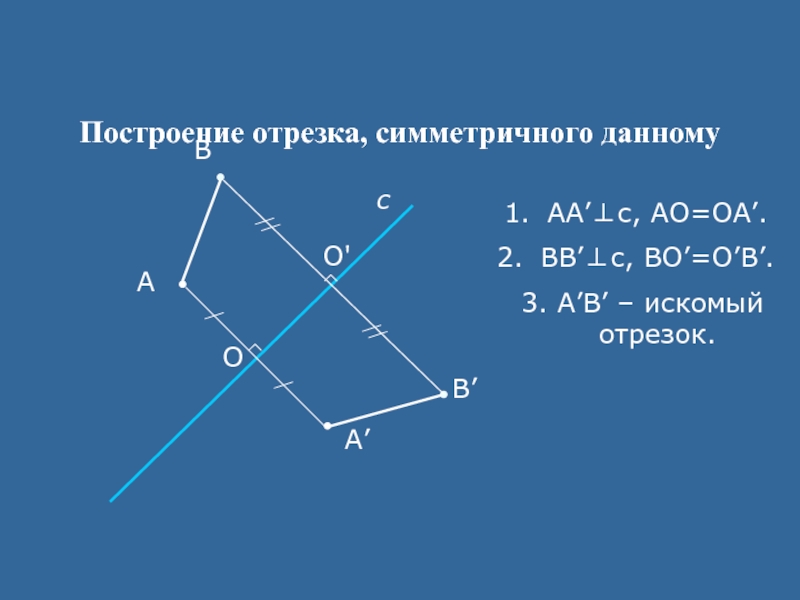
- 14. Построение отрезка, симметричного данномуАсА’ВВ’OO'АА’⊥с, АО=ОА’.ВВ’⊥с, ВО’=О’В’.3. А’В’ – искомый отрезок.
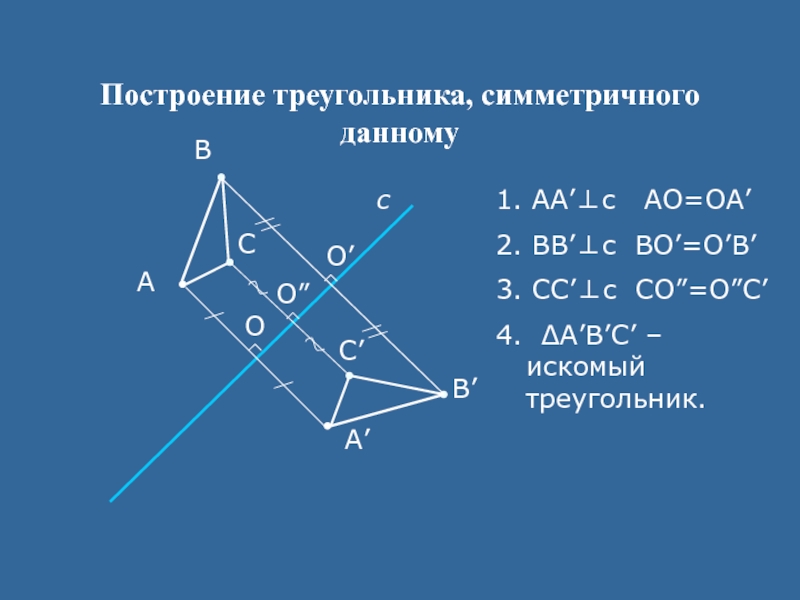
- 15. Построение треугольника, симметричного данномуАсА’ВВ’СС’1. AA’⊥c AO=OA’2. BB’⊥c BO’=O’B’3. СС’⊥c СO”=O”С’4. ΔA’B’С’ – искомый треугольник.OO”O’
- 16. LADCBEB1C1D1A1E1Построение фигуры, симметричной данной относительно оси симметрии
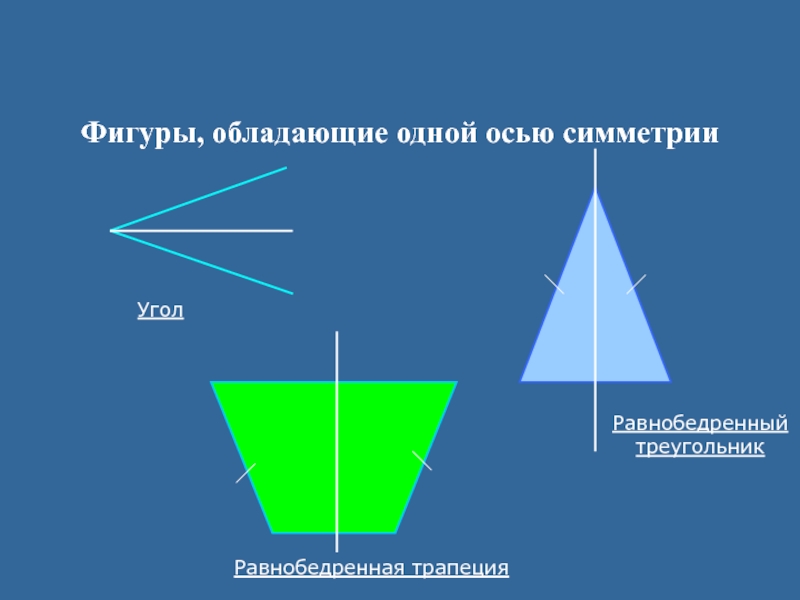
- 17. Фигуры, обладающие одной осью симметрииУголРавнобедренный треугольникРавнобедренная трапеция
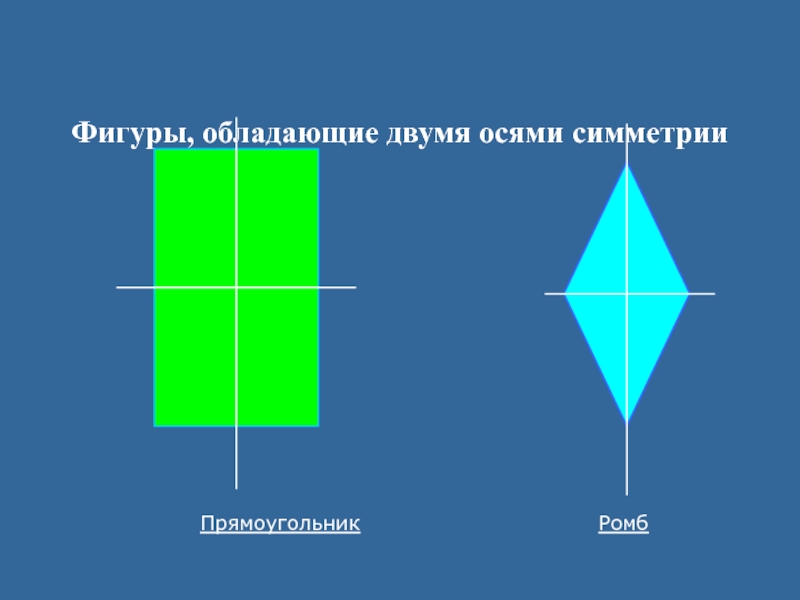
- 18. Фигуры, обладающие двумя осями симметрииПрямоугольникРомб
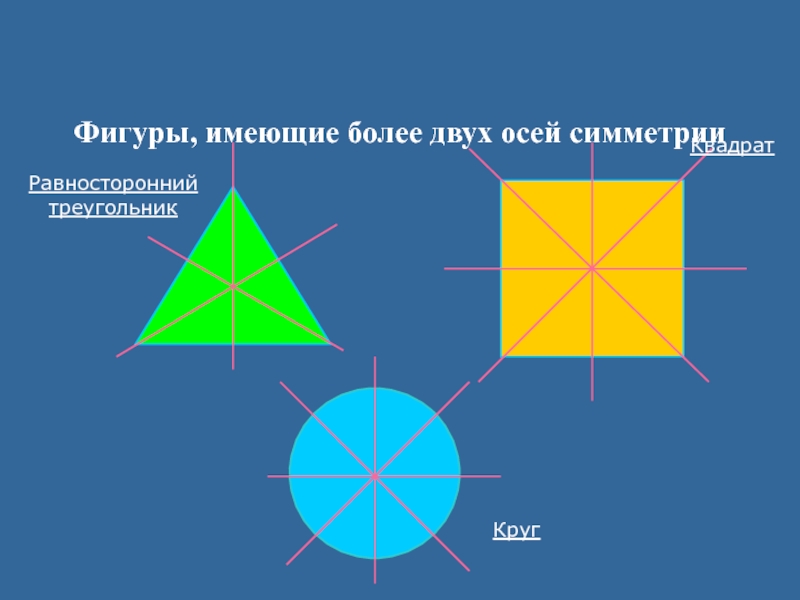
- 19. Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг
- 20. Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник
- 21. Заключение Симметрия многолика. Она обладает свойствами, которые
- 22. «Симметрия является той идеей, посредством которой человек
- 23. Скачать презентанцию
ОглавлениеЦентральная симметрия Осевая симметрияЗаключение
Слайды и текст этой презентации
Слайд 4Центральная симметрия
Две точки А и А1 называются симметричными относительно точки
О, если О - середина отрезка АА1. точка О
считается симметричной самой себе.
Слайд 5Построение точки, центрально-симметричной данной
А
Построить луч АО
Измерить длину отрезка АО
Отложить на
луче АО по другую сторону от точки О отрезок ОА1,
равный отрезку ОА.Точка А1 симметрична точке А относительно центра О.
Слайд 6Построение отрезка, центрально-симметричного данному
Построить луч АО
Измерить длину отрезка АО
Отложить на
луче АО по другую сторону от точки О отрезок ОА1,
равный отрезку ОА.Построить луч ВО
Измерить длину отрезка ВО
Отложить на луче ВО по другую сторону от точки О отрезок ОВ1, равный отрезку ОВ.
Соединить точки А1 и В1 отрезком
Слайд 7
Построение фигуры, центрально-симметричной данной
А
В
С
О
А1
В1
С1
Центрально-симметричные фигуры равны
Слайд 12Осевая симметрия
Преобразование фигуры F в фигуру F1, при котором каждая
ее точка переходит в точку, симметричную относительно данной прямой, называется
преобразованием симметрии относительно прямой а. Прямая а называется осью симметрии.
Слайд 14Построение отрезка, симметричного данному
А
с
А’
В
В’
O
O'
АА’⊥с, АО=ОА’.
ВВ’⊥с, ВО’=О’В’.
3. А’В’ – искомый отрезок.
Слайд 15Построение треугольника, симметричного данному
А
с
А’
В
В’
С
С’
1. AA’⊥c AO=OA’
2. BB’⊥c BO’=O’B’
3. СС’⊥c
СO”=O”С’
4. ΔA’B’С’ – искомый треугольник.
O
O”
O’
Слайд 17Фигуры, обладающие одной осью симметрии
Угол
Равнобедренный
треугольник
Равнобедренная трапеция
Слайд 20Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
Слайд 21Заключение Симметрия многолика. Она обладает свойствами, которые одновременно и просты, и
сложны, способны проявляться и единожды, и бесконечно много раз
Слайд 22«Симметрия является той идеей, посредством которой человек на протяжении веков
пытался постичь и создать порядок, красоту и совершенство»
Г.Вейль
